the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The point of no return for climate action: effects of climate uncertainty and risk tolerance
Matthias Aengenheyster
Qing Yi Feng
Frederick van der Ploeg
Henk A. Dijkstra
If the Paris Agreement targets are to be met, there may be very few years left for policy makers to start cutting emissions. Here we calculate by what year, at the latest, one has to take action to keep global warming below the 2 K target (relative to pre-industrial levels) at the year 2100 with a 67 % probability; we call this the point of no return (PNR). Using a novel, stochastic model of CO2 concentration and global mean surface temperature derived from the CMIP5 ensemble simulations, we find that cumulative CO2 emissions from 2015 onwards may not exceed 424 GtC and that the PNR is 2035 for the policy scenario where the share of renewable energy rises by 2 % year−1. Pushing this increase to 5 % year−1 delays the PNR until 2045. For the 1.5 K target, the carbon budget is only 198 GtC and there is no time left before starting to increase the renewable share by 2 % year−1. If the risk tolerance is tightened to 5 %, the PNR is brought forward to 2022 for the 2 K target and has been passed already for the 1.5 K target. Including substantial negative emissions towards the end of the century delays the PNR from 2035 to 2042 for the 2 K target and to 2026 for the 1.5 K target. We thus show how the PNR is impacted not only by the temperature target and the speed by which emissions are cut but also by risk tolerance, climate uncertainties and the potential for negative emissions. Sensitivity studies show that the PNR is robust with uncertainties of at most a few years.
The Earth system is currently in a state of rapid warming that is unprecedented even in geological records (Pachauri et al., 2014). This change is primarily driven by the rapid increase in atmospheric concentrations of greenhouse gases (GHGs) due to anthropogenic emissions since the industrial revolution (Myhre et al., 2013). Changes in natural physical and biological systems are already being observed (Rosenzweig et al., 2008), and efforts are made to determine the “anthropogenic impact” on particular (extreme weather) events (Haustein et al., 2016). Nowadays, the question is not so much if but by how much and how quickly the climate will change as a result of human interference, whether this change will be smooth or bumpy (Lenton et al., 2008) and whether it will lead to dangerous anthropogenic interference with the climate (Mann, 2009).
The climate system is characterized by positive feedbacks causing instabilities, chaos and stochastic dynamics (Dijkstra, 2013) and many details of the processes determining the future behavior of the climate state are unknown. The debate on action on climate change is therefore focused on the question of risk and how the probability of dangerous climate change can be reduced. In scientific and political discussions, targets on “allowable” warming (in terms of change in global mean surface temperature, GMST, relative to pre-industrial conditions1) have turned out to be salient. The 2 K warming threshold is commonly seen – while gauging considerable uncertainties – as a safe threshold to avoid the worst effects that might occur when positive feedbacks are unleashed (Pachauri et al., 2014). Indeed, in the Paris COP21 conference it was agreed to attempt to limit warming below 1.5 K (United Nations, 2015). It is, however, questionable whether the commitments made by countries (the so-called nationally determined contributions, NDCs) are sufficient to keep temperatures below the 1.5 K and possibly even the 2.0 K target (Rogelj et al., 2016a).
A range of studies has appeared to provide insight into the safe level of cumulative emissions to stay below either the 1.5 or 2.0 K target at a certain time in the future with a specified probability, usually taken as the year 2100. The choice of a particular year is necessarily arbitrary and neglects the possibility of additional future warming. Early studies made use of Earth System Models of Intermediate Complexity (EMICs; Huntingford et al., 2012; Steinacher et al., 2013; Zickfeld et al., 2009) to obtain such estimates. Because it was found that peak warming depends on cumulative carbon emissions, EΣ, but is independent of the emission pathway (Allen et al., 2009; Zickfeld et al., 2012), focus has been on the specification of a safe level of EΣ values corresponding to a certain temperature target. In more recent papers, also emulators derived from either C4MIP models (Sanderson et al., 2016) or CMIP5 (Coupled Model Intercomparison Project 5) models (Millar et al., 2017b), with specified emission scenarios, were used for this purpose. Such a methodology was recently used in Millar et al. (2017a) to argue that a post-2015 value of EΣ≈200 GtC would limit post-2015 warming to less than 0.6 ∘C (so meeting the 1.5 K target) with a probability of 66 %.
In this paper we pose the following question: assume one wants to limit warming to a specific threshold in the year 2100, while accepting a certain risk tolerance of exceeding it, then when, at the latest, does one have to start to ambitiously reduce fossil fuel emissions? The point in time when it is “too late” to act in order to stay below the prescribed threshold is called the point of no return (PNR; van Zalinge et al., 2017). The value of the PNR will depend on a number of quantities, such as the climate sensitivity and the means available to reduce emissions. To determine estimates of the PNR, a model is required of global climate development that (a) is accurate enough to give a realistic picture of the behavior of GMST under a wide range of climate change scenarios, (b) is forced by fossil fuel emissions, (c) is simple enough to be evaluated for a very large number of different emission and mitigation scenarios and (d) provides information about risk, i.e., it cannot be purely deterministic.
The models used in van Zalinge et al. (2017) are clearly too idealized to determine adequate estimates of the PNR under different conditions. In this paper, we therefore construct a stochastic state-space model from the CMIP5 results where many global climate models were subjected to the same forcing for a number of climate change scenarios (Taylor et al., 2012). This stochastic model – representing all kinds of uncertainties in the climate model ensemble – is then used together with a broad range of mitigation scenarios to determine estimates of the PNR under different risk tolerances.
Stocker (2013) showed that if the Paris Agreement temperature targets are to be met, only a few years are left for policy makers to take action by cutting emissions: with an emissions reduction rate of 5 % year−1, the 1.5 K target has become unachievable and the 2 K target becomes unachievable after 2017. The Stocker (2013) analysis highlights the crucial concept of the closing door or PNR of climate policy, but it is deterministic. It does not take account of the possibility that these targets are not met, and does not allow for negative emissions scenarios. We here show how the considerable climate uncertainties captured by our stochastic state-space model, the degree to which policy makers are willing to take risk, and the potential of negative emissions affect the carbon budget and the date at which climate policy becomes unachievable (the PNR). The climate policy is here not defined as an exponential emission reduction as in Stocker (2013) but as a steady increase in the share of renewable energy in total energy generation.
We let ΔT be the annual-mean area-weighted global mean surface temperature (GMST) deviation from pre-industrial conditions of which the 1861–1880 mean is considered to be representative (Pachauri et al., 2014; Schurer et al., 2017). From the CMIP5 scenarios we use the simulations of the pre-industrial control, abrupt quadrupling of atmospheric CO2, smooth increase of 1 % CO2 year−1 and the RCP (representative concentration pathway) scenarios 2.6, 4.5, 6.0 and 8.5 (Taylor et al., 2012). The data are obtained from the German Climate Computing Center (DKRZ), the ESGF Node at the DKRZ and KNMI's Climate Explorer. The CO2 forcings (concentrations, Meinshausen et al., 2011; and emissions, Clarke et al., 2007; Fujino et al., 2006; Riahi et al., 2007; van Vuuren et al., 2007) are obtained from the RCP Database (available at http://tntcat.iiasa.ac.at/RcpDb, last access: 28 March 2017).
As all CMIP5 models are designed to represent similar (physical) processes but use different formulations, parameterizations, resolutions and implementations, the results from different models offer a glimpse into the (statistical) properties of future climate change, including various forms of uncertainty. We perceive each model simulation as one possible, equally likely, realization of climate change. Applying ideas and methods from statistical physics (Ragone et al., 2016), in particular linear response theory (LRT), a stochastic model is constructed that represents the CMIP5 ensemble statistics of GMST.
2.1 Linear response theory
We only use those ensemble members from CMIP5 for which the control run and at least one perturbation run are available, leading to 34 members for the abrupt (CO2 quadrupling) and 39 for the smooth-forcing experiment. Considering those members from the RCP runs also available in the abrupt forcing run, we have 25 members for RCP2.6, 30 for RCP4.5, 19 for RCP6.0 and 29 for RCP8.5.
The CO2 concentration as a function of time for the abrupt quadrupling and smooth CO2 increase is prescribed as
with time in years from the start of the forcing, pre-industrial CO2 concentration C0 and Heaviside function θ(t). The radiative forcing ΔF due to CO2 relative to pre-industrial conditions is given as
with Wm−2 (Myhre et al., 2013). With LRT, the Green's function for the temperature response is computed from the abrupt forcing case as the time derivative of the mean response (Ragone et al., 2016)
where . The temperature deviation from the pre-industrial state for any forcing ΔFany is then obtained, via the convolution of the Green's function, as
Because Eq. (4) is exact, we expect that Eq. (5) with ΔFany=ΔFabrupt will exactly reproduce the abrupt CMIP5 response. In addition, for the LRT to be a useful approximation, the response has to reasonably reproduce the smooth 1 % year−1 CMIP5 response with ΔFany=ΔFsmooth. Figure 1a shows that LRT applied to the abrupt perturbation perfectly recovers the abrupt response – as required – and is well able to recover the response to a smooth forcing. The correspondence is very good for the mean response and also the variance is captured quite well.

Figure 1Ensemble mean (a) and variance (b) of temperature response from CMIP5 (solid) and LRT reproduction (dashed). Year 0 gives the start of the perturbation. (c) Reconstruction of RCP temperature evolution from concentration pathways using CO2 only. Blue, orange and green lines gives CMIP5 data for RCP4.5, RCP6.0 and RCP8.5, respectively, with the ensemble mean given in black solid (RCP4.5), dotted (RCP6.0) and dashed (RCP8.5) black. Reconstruction using CO2 radiative forcing in red (RCP4.5), purple (RCP6.0) and brown (RCP8.5).
Beyond finding the temperature change as a result of CO2 variations, eventually emissions, , cause these CO2 changes and have to be addressed explicitly. A multi-model study of many carbon models of varying complexity under different background states and forcing scenarios was recently presented Joos et al. (2013). A fit of a three-timescale exponential with constant offset was proposed for the ensemble mean of responses to a 100 GtC emission pulse to a present-day climate of the form
Coefficients and timescales are determined using least-square fits on the multi-model mean. The CO2 concentration then follows from
In doing so, we use a response function that is independent of the size of the impulse, i.e., the carbon cycle reacts in the same way to pulses of all sizes other than 100 GtC. This is of course a simplification, especially as very large pulses might unleash positive feedbacks to do with the saturation of natural sinks such as the oceans (Millar et al., 2017b), but works reasonably well in the range of emissions we are primarily interested in.
The full (temperature and carbon) LRT model is summarized as
and relates fossil CO2 emissions, , to mean GMST perturbation ΔT with initial conditions for CO2 and ΔT0 for GMST perturbation. This is quite a simple model with few “knobs to turn”. The only really free parameter is the constant A that scales up CO2-radiative forcing to take into account non-fossil CO2 and non-CO2 GHG emissions (not present in the idealized scenarios), and matches the carbon and temperature models (estimated from different model ensembles) together.
The constant A=1.48 was found in order to optimize the agreement of ΔT with CMIP5 RCPs. The resulting reconstruction of temperatures from RCP CO2 concentrations overlaid with CMIP5 data (Fig. 1c) gives a good agreement.
Table 1Stochastic state-space model. Carbon model on the left, temperature model on the right. Wt denotes the Wiener process.
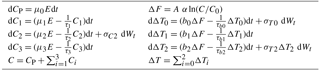
Internally, emissions need to be converted from GtC year−1 to ppm year−1 using the respective molar masses and the mass of the Earth's atmosphere as ppm year−1 = GtC year−1 with γ=0.46969 ppm GtC−1. Our estimates of the model's 10 parameters are found in Table 2.
Table 2Stochastic state-space model parameters. All timescales are in years, the carbon model amplitudes μi are dimensionless for E in (ppm year−1) and the temperature model amplitudes bi are in (K year−1 W−1m2).

In Fig. 2 we show the results obtained for RCP emissions. For very-high-emission scenarios we underestimate CO2 concentrations because for such emissions natural sinks saturate, which is a process the pulse-size independent carbon response function cannot adequately capture. However, the upscaling of radiative forcing is quite successful, yielding a good temperature reconstruction.
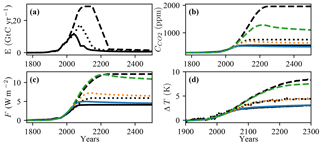
Figure 2Reconstruction of RCP results using the response function model. In all panels, solid lines refer to RCP4.5, dotted to RCP6.0 and dashed lines to RCP8.5. Black lines show RCP data while colors (blue: RCP4.5, orange: RCP6.0, green: RCP8.5) give our reconstruction. (a) Fossil CO2 emissions. (b) CO2 concentrations from RCP and reconstructed using . (c) Total anthropogenic radiative forcing (black) and radiative forcing from CO2 only (red) (both from RCP) and reconstructed forcing using the relations above. (d) Temperature perturbation from CMIP5 RCP (ensemble mean) and the our reconstruction.
2.2 Stochastic state-space model
The model outlined above still contains a data-based temperature response function and it informs only about the mean CMIP5 response. However, our main motivation is to obtain new insights into the possible evolution to a “safe” carbon-free state and such paths necessarily depend strongly on the variance of the climate and on the risk one is willing to take. This variance in temperature is quite substantial, as is evident from Fig. 1b and c. Therefore we translate our response function model to a stochastic state-space model and incorporate the variance via suitable stochastic terms.
The response function GT from the 140-year abrupt quadrupling ensemble is well approximated by
Although τb0→∞, we require a finite τb0 for temperatures to stabilize at some level. Hence, we choose a long timescale τb0=400 years that cannot really be determined from the 140-year abrupt forcing (CMIP5) runs. By writing
the LRT model can be transformed into the 7-dimensional stochastic state-space model (SSSM) shown in Table 1 with parameters in Table 2. Initial conditions are obtained by running the noise-free model forward from pre-industrial conditions (CP=C0 and ) to present-day, driven by historical emissions2. As these temperatures are now given relative to the start of emissions, i.e., 1765, we add the 1961–1990 model mean to the HadCRUT4 dataset to get observed temperature deviation relative to 1765, and compute ΔT relative to 1861–1880 by adding the 1861–1880 mean of this deviation time series.
The major benefit of this formulation is that we can include stochasticity. We introduce additive noise to the carbon model such that the standard deviation of the model response to an emission pulse as reported by Joos et al. (2013) is recovered. For the temperature model we introduce (small) additive noise to recover the (small) CMIP5 control run standard deviation. In the CMIP5 RCP runs the ensemble variance increases with rising ensemble mean. This calls for the introduction of (substantial) multiplicative noise, which we introduce in ΔT2, letting these random fluctuations decay over an 8-year timescale. The magnitude of these fluctuations is (especially at high temperatures) likely to be unrealistic when looking at individual time series. However, the focus here is on ensemble statistics.
2.3 Transition pathways
The SSSM described in the previous section is forced with fossil CO2 emissions. We assume that, in the absence of any mitigation actions, emissions increase from their initial value E0 at an exponential rate g=0.01 year−1 due to economic and population growth. Political decisions cause emissions to decrease from starting year ts onward as fossil energy generation is replaced by non-GHG producing forms such as wind, solar and water (mitigation m) and by an increasing share of fossil energy sources the emissions of which are not released but captured and stored away by carbon capture and storage (abatement m).
In addition, negative emission technologies may be employed. They cause a direct reduction in atmospheric CO2 concentration and are here modeled as an exponential3 . We model this in a very simple way by letting both mitigation and abatement increase linearly until emissions are brought to zero:
with constants m0 and a0 respectively giving the mitigation and abatement rates at the start of the scenario and m1 the incremental year-to-year increase. The simplified model (Eq. 14) is very well able (not shown) to reproduce the integrated assessment model (IAM) pathways that fulfill the NDCs until 2030 and afterwards reach the 2 K target with a 50–66 % probability (Rogelj et al., 2016a). These pathways are exemplary for those that continue on the low-commitment path for a while, followed by strong and decisive action. From them we obtain a family of negative emission scenarios out of which we pick a pathway with strong negative emissions. Using the starting year 2061, it is very well approximated by setting GtC and r=0.0283 year−1.
2.4 Point of no return
With the emission scenarios and the SSSM – returning CO2 concentrations and GMST for any such scenario – one can now address the issue of transitioning from the present-day (year 2015) to a carbon-free era such as to avoid catastrophic climate change. We need to take into account both the target threshold and the risk one is willing to take to exceed it. The maximum amount of cumulative CO2 emissions that allows for reaching the 1.5 and 2 K targets, as a function of the risk tolerance, is called the safe carbon budget (SCB). It is well established in the literature (Meinshausen et al., 2009; Zickfeld et al., 2009) but does not contain information on how these emissions are spread in time. This is where the PNR comes in: the PNR is the point in time where starting mitigating action is insufficient to stay below a specified target with a chosen risk tolerance.
Concretely, let the temperature target ΔTmax be the maximum allowable warming and denote the parameter β as the probability of staying below a given target (a measure of the risk tolerance). For example, the case ΔTmax=2 K and β=0.9 corresponds to a 90 % probability of staying below 2 K warming, i.e., 90 of 100 realizations of the SSSM, started in 2015 and integrated until 2100, do not exceed 2 K in the year 2100.
Then, in the context of Eq. (14), the PNR is the earliest ts that does not result in reaching the defined “Safe State” (van Zalinge et al., 2017) in terms of ΔTmax and β. It is determined from the probability distribution p(ΔT2100) of GMST in 2100.
Both SCB and PNR depend on temperature target, climate uncertainties and risk tolerance, but the PNR also depends on the aggressiveness of the climate action considered feasible (here given by the value of m1). This makes the PNR such an interesting quantity, since the SCB does not depend on the time path of emission reductions.
Clearly there is a close connection between the PNR and the SCB. Indeed, one could define a PNR also in terms of the ability to reach the SCB. The one-to-one relation between cumulative emissions and warming gives the PNR in “carbon space”. Its location in time, however, depends crucially on how fast a transition to a carbon-neutral economy is feasible.
For details on the scenarios, we refer to Rogelj et al. (2016a). With carbon budgets rapidly running out and the PNR approaching fast, negative emissions may have to become an essential part of the policy mix. Such policies are cheap but may only be a temporary fix and lead to undesirable spillover effects on neighboring countries (e.g., Wagner and Weitzman, 2015). We abstract from these discussions here since this is beyond the scope of the present paper.
To demonstrate the quality of the SSSM we initialize it at pre-industrial conditions, run it forward and compare the results with those of CMIP5 models. The SSSM is well able to reproduce the CMIP5 model behavior under the different RCP scenarios (Fig. 3, shown for RCP2.6 and RCP4.5). As these scenarios are very different in terms of rate of change and total cumulative emissions, this is not a trivial finding. It is actually remarkable that the SSSM, which is based on a limited amount of CMIP5 model ensemble members, performs so well. As an example, the RCP2.6 scenario contains substantial negative emissions, responsible for the downward trend in GMST, which our SSSM correctly reproduces. The mean response for RCP8.5 is slightly underestimated (not shown) because the uncertainty in the carbon cycle plays a rather minor role compared to that in the temperature model. In addition, for such large emission reductions, positive feedback loops set in from which our SSSM abstracts. The temperature perturbation ΔT is very closely log-normally distributed, while for weak forcing scenarios (e.g., RCP2.6 and RCP4.5) the distribution is approximately Gaussian. The CO2 concentration is found to be Gaussian distributed for all RCP scenarios. These findings (log-normal temperature and Gaussian CO2 concentration) result from the multiplicative and additive noise in temperature and carbon components of the SSSM, respectively.
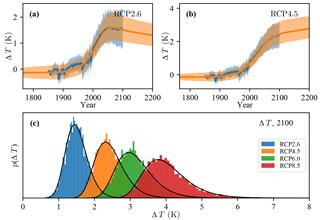
Figure 3Stochastic state-space model applied to RCP scenarios. (a, b) Ensemble mean and 5th and 95th percentile envelopes of CMIP5 RCPs (blue) and stochastic model (orange). (c) Probability density functions for ΔT in 2100 based on 5000 ensemble members, and driven by forcing from RCP2.6 (blue), RCP4.5 (orange), RCP6.0 (green) and RCP8.5 (red). In black are fitted log-normal distributions.
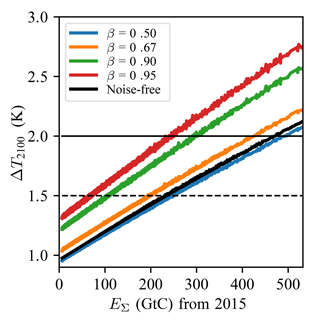
Figure 4The safe carbon budget. ΔTmax in 2100 such that as a function of cumulative emissions for different β. The black curve gives the deterministic results with noise terms in the stochastic model set to zero.
To determine the SCB, 6000 emission reduction strategies (with Eneg(t)=0) were generated and, using the SSSM, an 8000-member ensemble for each of these emission scenarios starting in 2015 was integrated. Emission scenarios are generated from Eq. (14) by letting a(t)=0, a uniform and m1 drawn from a beta distribution (with distribution function , where B(α,δ) is the beta function; parameters are chosen as ), with the [0,1] interval scaled such that m=1 at the latest in 2080. The beta distribution is chosen for practical reasons to sample (m0,m1) pairs. As m0 is drawn from a uniform distribution, doing likewise for m1 would result in many pathways with very quick mitigation and low cumulative emissions. Choosing a beta distribution for m1 makes draws of small m1 much more likely and leads to a better sampling of high cumulative emission scenarios. The choice of distribution has no consequences on the results.
The temperature anomaly in 2100 (ΔT2100) as a function of cumulative CO2 emissions EΣ is shown in Fig. 4. The same calculation is also shown for the deterministic case without climate uncertainty (no noise in the SSSM). In Fig. 4, the SCB is given by the point on the EΣ axis where the (colored) line corresponding to a chosen risk tolerance crosses the (horizontal) line corresponding to a chosen temperature threshold ΔTmax. The curves ΔT2100=f(EΣ) (Fig. 4) are very well described by expressions of the type
with suitable coefficients a,b and c, each depending on the tolerance β. For the range of emissions considered here, a linear fit would be reasonable (Allen et al., 2009). However, our expression also works for cumulative emissions in the range of business as usual (when fitting parameters on suitable emission trajectories). From Fig. 4 we easily find the SCB for any combination of ΔTmax and β, as shown in Table 3.
Allowable emissions are drastically reduced when enforcing the target with a higher probability (following the horizontal lines from right to left in Fig. 4). These results show in particular the challenges posed by the 1.5 K compared to the 2 K target.
From IPCC-AR5 (IPCC, 2013) we find cumulative emissions post-2015 of 377 to 517 GtC in order to “likely” stay below 2 K while we find an SCB of 424 GtC for ΔTmax=2 K and β=0.67 which lies in the same range. Like Millar et al. (2017a) we find approximately 200 GtC to stay below 1.5 K with β=0.67.
To determine the PNR, we resort to three illustrative choices to model the abatement and mitigation rates with Eneg(t)=0.
Following Eq. (14) we construct fast mitigation (FM) and moderate mitigation (MM) scenarios with m1=0.05 and 0.02, respectively. In addition, in an extreme mitigation (EM) scenario m=1 can be reached instantaneously. This corresponds to the most extreme physically possible scenario and serves as an upper bound.
When varying ts to find the PNR for the three scenarios, we always keep m0=0.14 and a0=0 at 2015 values (World Energy Council, 2016).
As an example, ts=2025 leads to total cumulative emissions from 2015 onward of 109, 183 and 335 GtC for the mitigation scenarios EM, FM and MM, respectively. MM is the most modest scenario, but it is actually quite ambitious, considering that with m=0.1355 in 2005 and m=0.14 in 2015 (World Energy Council, 2016) the current year-to-year increases in the share of renewable energies are very small.
Figure 5 shows the probabilities for staying below the 1.5 and 2 K thresholds in 2100 as a function of ts for different policies, including FM (m1=0.05) and MM (m1=0.02), while the EM policy bounds the unachievable region. It is clear that this region is larger for the 1.5 K than for the 2.0 K target, and shrinks when including negative emissions. From the plot we can directly see the consequences of delaying action until a given year. For example, if policy makers should choose to implement the MM strategy only in 2040, the chances of reaching the 1.5 K (2.0 K) target are only 2 % (47 %). We conclude that the remaining “window of action” may be small, but a window still exists for both targets. For example, the 2 K target is reached with a probability of 67 % even when starting MM is delayed until 2035. However, reaching the 1.5 K target appears unlikely as MM would be required to start in 2018 for a probability of 67 %. When requiring a high (≥0.9) probability, it is impossible to reach with the MM scenario. The PNR for the different targets and probabilities is shown in Table 4 and Fig. 5.
Table 4Point of no return as a function of threshold and safety probability β without and with strong negative emissions.
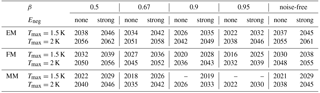
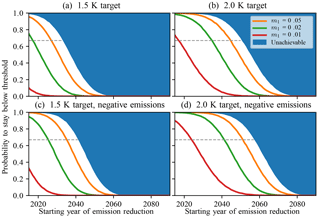
Figure 5The point of no return. Probability of staying below the 1.5 K (a, c) or 2.0 K (b, d) threshold when starting emission reductions in a given year, for different policies as described by Eq. (14) with different choices for m1, the rate of mitigation increase per year. Top and bottom panels show the cases without and with strong negative emissions, respectively. The point of no return for a given policy is given by the point in time where the probability drops below a chosen threshold. The default threshold of two-thirds is dashed. The unachievable region is bounded by the extreme mitigation scenario.
Including strong negative emissions delays the PNR by 6–10 years, which may be very valuable especially for ambitious targets. For example, one can then reach 1.5 K with a probability of up to 66 % in the MM scenario when acting before 2026, 8 years later than without.
The PNR varies substantially for slightly different temperature targets. This also illustrates the importance of the temperature baseline relative to which ΔT is defined, as has been found previously (Schurer et al., 2017). Switching to a (lower) 18th century baseline increases current levels of warming by 0.13 K (Schurer et al., 2017) and thereby brings forward the PNR. For example, for a maximum temperature threshold of 1.5 K, the PNR moves from 2022 to 2016 in the MM scenario and from 2038 to 2033 for the EM scenario.
It is clear that an energy transition more ambitious than RCP2.6 is required to stay below 1.5 K with some acceptable probability, and whether that is feasible is doubtful. For all other RCP scenarios, exceeding 2 K is very likely in this century (Fig. 6).
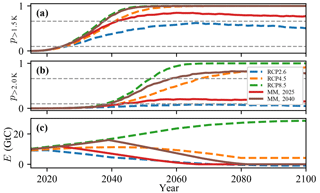
Figure 6(a, b) Instantaneous probability to exceed 1.5 K (a) and 2.0 K (b) for different emission scenarios. RCP scenarios are shown as dashed lines while solid lines give MM scenario results starting in 2025 (red) and 2040 (brown). Dashed horizontal lines give p=0.1 and 0.67, respectively. (c) Fossil fuel emissions in GtC for the same scenarios.
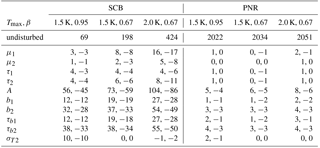
The parameter sensitivities of SCB and PNR were determined by varying each parameter by ±5 %. Table 5 shows the results for selected parameters for a small (Tmax=1.5 K, β=0.95), intermediate (Tmax=1.5 K, β=0.5) and large (Tmax=2 K, β=0.5) SCB, corresponding to a close, intermediate and far PNR.
The biggest sensitivities are found for the radiative forcing parameter A. The parameters of the carbon model (μi,τi) do not have big impacts on the found SCB, on the order of 0–17 GtC, with larger numbers found for larger absolute values of SCB. The temperature-model parameters are more important, changing the SCB by up to around 10 % for large and 50 % for small values. The model is particularly sensitive to changes in the intermediate timescale (b2,τb2). The PNR sensitivities are generally small. We find the most relevant, yet small, sensitivities in the temperature model parameters. For example, a 10 % error in τb2 can move the PNR by 3–4 years.
The sensitivity of SCB and PNR to the noise amplitudes is small, with largest values found for the multiplicative noise amplitude σT2 that is responsible for most of the spread of the temperature distribution. Increasing noise amplitudes decreases the SCB, in accordance with the expectation that larger climate uncertainty leads to tighter constraints.
It is useful to remember that the stochastic formulation of our model is designed with the explicit purpose to incorporate parameter uncertainty in a natural way via the noise term, without having to make specific assumptions on the uncertainties of individual parameters.
Table 5Sensitivity of the safe carbon budget (SCB) and point of no return (PNR) to selected parameter variations. Values as difference in GtC (SCB) and number of years (PNR) relative to the undisturbed value (top row). The PNR values all refer to the EM scenario. First and second numbers give 10 % parameter decrease and increase, respectively.
We have developed a novel stochastic state-space model (SSSM) to accurately capture the basic statistical properties (mean and variance) of the CMIP5 RCP ensemble, allowing us to study warming probabilities as a function of emissions. It represents an alternative to the approach that contains stochasticity in the parameters rather than the state. Although the model is highly idealized, it captures simulations of both temperature and carbon responses to RCP emission scenarios quite well.
A weakness of the SSSM is the simulation of temperature trajectories beyond 2100 and for high-emission scenarios. The large multiplicative noise factor leads – especially at high mean warmings – to immensely volatile trajectories that in all likelihood are not physical (on the individual level, the distribution is still well-behaved). It might be worthwhile to investigate how this could be improved. Another weakness in the carbon component of the SSSM is that the real carbon cycle is not pulse-size independent. Hence, using a single constant response function has inherent problems, in particular when running very high-emission scenarios. This is because the efficiency of the natural carbon sinks to the ocean and land reservoirs is a function of both temperature and the reservoir sizes. The SSSM therefore has slight problems reproducing CO2 concentration pathways (Fig. 2), a price we accept to pay as we focus on the CMIP5 temperature reproduction.
Taking account of non-CO2 emissions more fully beyond our simple scaling and also avoiding temporary overshoots of the temperature caps would reduce the carbon budgets (Rogelj et al., 2016b) and thus lead to earlier PNRs than given here. Therefore the values might be a little too optimistic.
In Millar et al. (2017b), the authors draw a different conclusion from studying a similar problem. They introduce, in their FAIR model, response functions that dynamically adjust parameters based on warming to represent sink saturation. Consequently, their model gives much better results in terms of CO2 concentrations. It would be an interesting lead for future research to conduct our analysis (in terms of SCB and PNR) with other simple models (such as FAIR or MAGICC) to discover similarities and differences. However, only rather low-emission scenarios are consistent with the 1.5 or 2 K targets, so we do not expect such nonlinearities to play a major role, and indeed our carbon budgets are very similar to Millar et al. (2017a).
The concept of a point of no return introduces a novel perspective into the discussion of carbon budgets that is often centered on the question of when the remaining budget will have “run out” at current emissions. In contrast, the PNR concept recognizes the fact that emissions will not stay constant and can decay faster or slower depending on political decisions.
With these caveats in mind, we conclude that, first, the PNR is still relatively far away for the 2 K target: with the MM scenario and β=67 % we have 17 years left to start. When allowing for setting all emissions to zero instantaneously, the PNR is even delayed to the 2050s. Considering the slow speed of large-scale political and economic transformations, decisive action is still warranted, as the MM scenario is a large change compared to current rates. Second, the PNR is very close or passed for the 1.5 K target. Here more radical action is required – 9 years remain to start the FM policy to avoid a 1.5 K increase with a 67 % chance, and strong negative emissions give us 8 years under the MM policy.
Third, we can clearly show the effects of changing ΔTmax,β and the mitigation scenario. Switching from 1.5 to 2 K buys an additional ∼16 years. Allowing a one-third, instead of a one-tenth, exceedance risk buys an additional 7–9 years. Allowing for the more aggressive FM policy instead of MM buys an additional 10 years. This allows us to assess trade-offs, for example, between tolerating higher exceedance risks and implementing more radical policies.
Fourth, negative emissions can offer a brief respite but only delay the PNR by a few years, not taking into account the possible decrease in effectiveness of these measures in the long term (Tokarska and Zickfeld, 2015).
In this work a large ensemble of simulations was used in order to average over stochastic internal variability. This allows us to determine the point in time where a threshold is crossed at a chosen probability level. Such an ensemble is not possible for more realistic models, nor do GCMs agree on details of internal variability. Therefore, in practice, the crossing of a threshold will likely be determined with hindsight and using long temporal means. This fact should lead us to be more cautious in choosing mitigation pathways.
We have shown the constraints put on future emissions by restricting GMST increase below 1.5 or 2 K, and the crucial importance of the safety probability. Further (scientific and political) debate is essential on what are the right values for both temperature threshold and probability. Our findings are sobering in light of the bold ambition in the Paris Agreement, and add to the sense of urgency to act quickly before the PNR has been crossed.
The study is based on publicly available data sets as described in the Methods section. Model and analysis scripts and outputs are available on request from the corresponding author.
MA and HAD developed the research idea, MA developed the model and performed the analysis. All authors discussed the results and contributed to the writing of the paper.
The authors declare that they have no conflict of interest.
We thank the focus area “Foundations of Complex Systems” of Utrecht
University for providing the finances for the visit of Frederick van der
Ploeg to Utrecht in 2016. Matthias Aengenheyster is thankful for support by the German Academic Scholarship Foundation.
Henk A. Dijkstra acknowledges support by the
Netherlands Earth System Science Centre (NESSC), financially supported by the
Ministry of Education, Culture and Science (OCW), Grant
no. 024.002.001.
Edited by: Christian Franzke
Reviewed by: two anonymous referees
Allen, M. R., Frame, D. J., Huntingford, C., Jones, C. D., Lowe, J. A., Meinshausen, M., and Meinshausen, N.: Warming caused by cumulative carbon emissions towards the trillionth tonne, Nature, 458, 1163–1166, https://doi.org/10.1038/nature08019, 2009. a, b
Clarke, L. E., Edmonds, J. A., Jacoby, H. D., Pitcher, H. M., Reily, J. M., and Richels, R. G.: Scenarios of Greenhouse Gas Emissions and Atmospheric Concentrations Synthesis, Tech. rep., Department of Energy, Office of Biological & Environmental Research, Washington, DC, 2007. a
Dijkstra, H. A.: Nonlinear Clim. Dynam., Cambridge University Press, Cambridge, https://doi.org/10.1017/CBO9781139034135, 2013. a
Fujino, J., Nair, R., Kainuma, M., Masui, T., and Matsuoka, Y.: Multi-gas Mitigation Analysis on Stabilization Scenarios Using Aim Global Model, Energ. J., 2006, 343–354, https://doi.org/10.5547/ISSN0195-6574-EJ-VolSI2006-NoSI3-17, 2006. a
Haustein, K., Otto, F. E. L., Uhe, P., Schaller, N., Allen, M. R., Hermanson, L., Christidis, N., McLean, P., and Cullen, H.: Real-time extreme weather event attribution with forecast seasonal SSTs, Environ. Res. Lett., 11, 064006, https://doi.org/10.1088/1748-9326/11/6/064006, 2016. a
Huntingford, C., Lowe, J. A., Gohar, L. K., Bowerman, N. H. A., Allen, M. R., Raper, S. C. B., and Smith, S. M.: The link between a global 2∘C warming threshold and emissions in years 2020, 2050 and beyond, Environ. Res. Lett., 7, 014039, 2012. a
IPCC: Climate Change 2013 – The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, https://doi.org/10.1017/CBO9781107415324, 2013. a
Joos, F., Roth, R., Fuglestvedt, J. S., Peters, G. P., Enting, I. G., von Bloh, W., Brovkin, V., Burke, E. J., Eby, M., Edwards, N. R., Friedrich, T., Frölicher, T. L., Halloran, P. R., Holden, P. B., Jones, C., Kleinen, T., Mackenzie, F. T., Matsumoto, K., Meinshausen, M., Plattner, G.-K., Reisinger, A., Segschneider, J., Shaffer, G., Steinacher, M., Strassmann, K., Tanaka, K., Timmermann, A., and Weaver, A. J.: Carbon dioxide and climate impulse response functions for the computation of greenhouse gas metrics: a multi-model analysis, Atmos. Chem. Phys., 13, 2793–2825, https://doi.org/10.5194/acp-13-2793-2013, 2013. a, b
Le Quéré, C., Andrew, R. M., Canadell, J. G., Sitch, S., Korsbakken, J. I., Peters, G. P., Manning, A. C., Boden, T. A., Tans, P. P., Houghton, R. A., Keeling, R. F., Alin, S., Andrews, O. D., Anthoni, P., Barbero, L., Bopp, L., Chevallier, F., Chini, L. P., Ciais, P., Currie, K., Delire, C., Doney, S. C., Friedlingstein, P., Gkritzalis, T., Harris, I., Hauck, J., Haverd, V., Hoppema, M., Klein Goldewijk, K., Jain, A. K., Kato, E., Körtzinger, A., Landschützer, P., Lefèvre, N., Lenton, A., Lienert, S., Lombardozzi, D., Melton, J. R., Metzl, N., Millero, F., Monteiro, P. M. S., Munro, D. R., Nabel, J. E. M. S., Nakaoka, S.-I., O'Brien, K., Olsen, A., Omar, A. M., Ono, T., Pierrot, D., Poulter, B., Rödenbeck, C., Salisbury, J., Schuster, U., Schwinger, J., Séférian, R., Skjelvan, I., Stocker, B. D., Sutton, A. J., Takahashi, T., Tian, H., Tilbrook, B., van der Laan-Luijkx, I. T., van der Werf, G. R., Viovy, N., Walker, A. P., Wiltshire, A. J., and Zaehle, S.: Global Carbon Budget 2016, Earth Syst. Sci. Data, 8, 605–649, https://doi.org/10.5194/essd-8-605-2016, 2016. a
Lenton, T. M., Held, H., Kriegler, E., Hall, J. W., Lucht, W., Rahmstorf, S., and Schellnhuber, H. J.: Tipping elements in the Earth's climate system, P. Natl. Acad. Sci. USA, 105, 1786–1793, https://doi.org/10.1073/pnas.0705414105, 2008. a
Mann, M. E.: Defining dangerous anthropogenic interference., P. Natl. Acad. Sci. USA, 106, 4065–4066, https://doi.org/10.1073/pnas.0901303106, 2009. a
Meinshausen, M., Meinshausen, N., Hare, W., Raper, S. C. B., Frieler, K., Knutti, R., Frame, D. J., and Allen, M. R.: Greenhouse-gas emission targets for limiting global warming to 2 ∘C, Nature, 458, 1158–1162, https://doi.org/10.1038/nature08017, 2009. a
Meinshausen, M., Smith, S. J., Calvin, K., Daniel, J. S., Kainuma, M. L. T., Lamarque, J.-F., Matsumoto, K., Montzka, S. A., Raper, S. C. B., Riahi, K., Thomson, A., Velders, G. J. M., and van Vuuren, D. P.: The RCP greenhouse gas concentrations and their extensions from 1765 to 2300, Climatic Change, 109, 213–241, https://doi.org/10.1007/s10584-011-0156-z, 2011. a
Millar, R. J., Fuglestvedt, J. S., Friedlingstein, P., Rogelj, J., Grubb, M. J., Matthews, H. D., Skeie, R. B., Forster, P. M., Frame, D. J., and Allen, M. R.: Emission budgets and pathways consistent with limiting warming to 1.5 ∘C, Nat. Geosci., 10, 741–747, 2017a. a, b, c
Millar, R. J., Nicholls, Z. R., Friedlingstein, P., and Allen, M. R.: A modified impulse-response representation of the global near-surface air temperature and atmospheric concentration response to carbon dioxide emissions, Atmos. Chem. Phys., 17, 7213–7228, https://doi.org/10.5194/acp-17-7213-2017, 2017b. a, b, c
Myhre, G., Shindell, D., Bréon, F.-M., Collins, W., Fuglestvedt, J., Huang, J., Koch, D., Lamarque, J.-F., Lee, D., Mendoza, B., Nakajima, T., Robock, A., Stephens, T., Takemura, T., and Zhang, H.: Anthropogenic and Natural Radiative Forcing, in: Climate Change 2013 - The Physical Science Basis, edited by: Intergovernmental Panel on Climate Change, chap. 8, 659–740, Cambridge University Press, Cambridge, https://doi.org/10.1017/CBO9781107415324.018, 2013. a, b
Pachauri, R. K., Allen, M. R., Barros, V. R., Broome, J., Cramer, W., Christ, R., Church, J. A., Clarke, L., Dahe, Q., Dasgupta, P., Dubash, N. K., Edenhofer, O., Elgizouli, I., Field, C. B., Forster, P., Friedlingstein, P., Fuglestvedt, J., Gomez-Echeverri, L., Hallegatte, S., Hegerl, G., Howden, M., Jiang, K., Cisneroz, B. J., Kattsov, V., Lee, H., Mach, K. J., Marotzke, J., Mastrandrea, M. D., Meyer, L., Minx, J., Mulugetta, Y., O'Brien, K., Oppenheimer, M., Pereira, J. J., Pichs-Madruga, R., Plattner, G.-K., Pörtner, H.-O., Power, S. B., Preston, B., Ravindranath, N. H., Reisinger, A., Riahi, K., Rusticucci, M., Scholes, R., Seyboth, K., Sokona, Y., Stavins, R., Stocker, T. F., Tschakert, P., van Vuuren, D., and van Ypserle, J.-P.: Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, IPCC, Geneva, Switzerland, 2014. a, b, c
Ragone, F., Lucarini, V., and Lunkeit, F.: A new framework for climate sensitivity and prediction: a modelling perspective, Clim. Dynam., 46, 1459–1471, https://doi.org/10.1007/s00382-015-2657-3, 2016. a, b
Riahi, K., Grubler, A., and Nakicenovic, N.: Scenarios of long-term socio-economic and environmental development under climate stabilization, Technol. Forecast. Soc., 74, 887–935, https://doi.org/10.1016/j.techfore.2006.05.026, 2007. a
Rogelj, J., den Elzen, M., Höhne, N., Fransen, T., Fekete, H., Winkler, H., Schaeffer, R., Sha, F., Riahi, K., and Meinshausen, M.: Paris Agreement climate proposals need a boost to keep warming well below 2 ∘C, Nature, 534, 631–639, https://doi.org/10.1038/nature18307, 2016a. a, b, c
Rogelj, J., Schaeffer, M., Friedlingstein, P., Gillett, N. P., van Vuuren, D. P., Riahi, K., Allen, M., and Knutti, R.: Differences between carbon budget estimates unravelled, Nat. Clim. Change, 6, 245–252, https://doi.org/10.1038/nclimate2868, 2016b. a
Rosenzweig, C., Karoly, D., Vicarelli, M., Neofotis, P., Wu, Q., Casassa, G., Menzel, A., Root, T. L., Estrella, N., Seguin, B., Tryjanowski, P., Liu, C., Rawlins, S., and Imeson, A.: Attributing physical and biological impacts to anthropogenic climate change, Nature, 453, 353–357, https://doi.org/10.1038/nature06937, 2008. a
Sanderson, B. M., O'Neill, B. C., and Tebaldi, C.: What would it take to achieve the Paris temperature targets?, Geophys. Res. Lett., 43, 7133–7142, https://doi.org/10.1002/2016GL069563, 2016. a
Schurer, A. P., Mann, M. E., Hawkins, E., Tett, S. F. B., and Hegerl, G. C.: Importance of the pre-industrial baseline for likelihood of exceeding Paris goals, Nat. Clim. Change, 7, 563–567, 2017. a, b, c
Steinacher, M., Joos, F., and Stocker, T. F.: Allowable carbon emissions lowered by multiple climate targets, Nature, 499, 197–201, 2013. a
Stocker, T. F.: The Closing Door of Climate Targets, Science, 339, 280–282, https://doi.org/10.1126/science.1232468, 2013. a, b, c
Taylor, K. E., Stouffer, R. J., and Meehl, G. A.: An Overview of CMIP5 and the Experiment Design, B. Am. Meteorol. Soc., 93, 485–498, https://doi.org/10.1175/BAMS-D-11-00094.1, 2012. a, b
Tokarska, K. B. and Zickfeld, K.: The effectiveness of net negative carbon dioxide emissions in reversing anthropogenic climate change, P. Natl. Acad. Sci. USA, 10, 1–11, 2015. a
United Nations: Adoption of the Paris Agreement, Framework Convention on Climate Change, 21st Conference of the Parties, Paris, 2015. a
van Vuuren, D. P., den Elzen, M. G. J., Lucas, P. L., Eickhout, B., Strengers, B. J., van Ruijven, B., Wonink, S., and van Houdt, R.: Stabilizing greenhouse gas concentrations at low levels: an assessment of reduction strategies and costs, Climatic Change, 81, 119–159, https://doi.org/10.1007/s10584-006-9172-9, 2007. a
van Zalinge, B. C., Feng, Q. Y., Aengenheyster, M., and Dijkstra, H. A.: On determining the point of no return in climate change, Earth Syst. Dynam., 8, 707–717, https://doi.org/10.5194/esd-8-707-2017, 2017. a, b, c
Wagner, G. and Weitzman, M. L.: Climate Shock: the Economic Consequences of a Hotter Planet, Princeton University Press, Princeton, New Jersey, 2015. a
World Energy Council: World Energy Resources 2016, Tech. rep., World Energy Council, London, 2016. a, b
Zickfeld, K., Eby, M., Matthews, H. D., and Weaver, A. J.: Setting cumulative emissions targets to reduce the risk of dangerous climate change, P. Natl. Acad. Sci. USA, 106, 16129–16134, https://doi.org/10.1073/pnas.0805800106, 2009. a, b
Zickfeld, K., Arora, V. K., and Gillett, N. P.: Is the climate response to CO2 emissions path dependent?, Geophys. Res. Lett., 39, https://doi.org/10.1029/2011GL050205, 2012. a






