the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Climate system response to stratospheric sulfate aerosols: sensitivity to altitude of aerosol layer
Krishna-Pillai Sukumara-Pillai Krishnamohan
Govindasamy Bala
Long Cao
Ken Caldeira
Reduction of surface temperatures of the planet by injecting sulfate aerosols in the stratosphere has been suggested as an option to reduce the amount of human-induced climate warming. Several previous studies have shown that for a specified amount of injection, aerosols injected at a higher altitude in the stratosphere would produce more cooling because aerosol sedimentation would take longer. In this study, we isolate and assess the sensitivity of stratospheric aerosol radiative forcing and the resulting climate change to the altitude of the aerosol layer. We study this by prescribing a specified amount of sulfate aerosols, of a size typical of what is produced by volcanoes, distributed uniformly at different levels in the stratosphere. We find that stratospheric sulfate aerosols are more effective in cooling climate when they reside higher in the stratosphere. We explain this sensitivity in terms of effective radiative forcing: volcanic aerosols heat the stratospheric layers where they reside, altering stratospheric water vapor content, tropospheric stability, and clouds, and consequently the effective radiative forcing. We show that the magnitude of the effective radiative forcing is larger when aerosols are prescribed at higher altitudes and the differences in radiative forcing due to fast adjustment processes can account for a substantial part of the dependence of the amount of cooling on aerosol altitude. These altitude effects would be additional to dependences on aerosol microphysics, transport, and sedimentation, which are outside the scope of this study. The cooling effectiveness of stratospheric sulfate aerosols likely increases with the altitude of the aerosol layer both because aerosols higher in the stratosphere have larger effective radiative forcing and because they have higher stratospheric residence time; these two effects are likely to be of comparable importance.
- Article
(7578 KB) -
Supplement
(3905 KB) - BibTeX
- EndNote
Anthropogenic emissions of greenhouse gases alter the radiative balance of the planet, leading to long-term climate changes (IPCC, 2013). Of particular interest is the warming from an increasing concentration of atmospheric carbon dioxide (CO2), which is the primary warming agent in the industrial era. Solar radiation management (also known as solar geoengineering) through albedo enhancement methods such as deliberate injection of sulfate aerosols into the stratosphere has been suggested as an option to counteract human-induced climate change (Budyko, 1977; Crutzen, 2006). In some such-envisioned geoengineering implementations, the positive radiative forcing from greenhouse gases would be partially or fully offset by negative radiative forcing from increased shortwave (SW) scattering by aerosols.
Major volcanic eruptions have been considered as a natural analogue to stratospheric sulfate aerosol geoengineering. Major volcanic eruptions inject the sulfate aerosol precursor SO2 into the stratosphere where it is converted to sulfate aerosols. These sulfate aerosol concentrations decay with an e-folding time of approximately 1 year (Robock, 2000). The increased scattering of SW radiation by the aerosols has a cooling effect on the climate system (Hansen et al., 1992; Robock, 2000; Soden et al., 2002). Volcanic eruptions are episodic, but for stratospheric aerosol geoengineering, the aerosol layer would need to be maintained with quasi-continuous injection of additional aerosols. The quasi-continuous injection can lead to particle growth where the newly injected particles coagulate with background particles, which can potentially lead to decreased scattering efficiency (Heckendorn et al., 2009; Niemeier et al., 2011; Niemeier and Timmreck, 2015; Tilmes et al., 2017).
The time evolution of radiative forcing and surface cooling per unit mass of injection of aerosols depends on several factors such as type of aerosol used (Pope et al., 2012; Weisenstein et al., 2015), particle size (Rasch et al., 2008; Heckendorn et al., 2009), amount of aerosols injected (Heckendorn et al., 2009; Niemeier and Timmreck, 2015; Kleinschmitt et al., 2018), and the geographical location and altitude of injection (Tilmes et al., 2017; Dai et al., 2018). One of the primary factors affecting the amount of cooling in geoengineering scenarios is aerosol particle size. For a specified mass, smaller particles are more efficient at scattering (Rasch et al., 2008; Heckendorn et al., 2009). As particles with radii in the range of 0.1 µm have the largest backscattering cross section per unit mass, they have been suggested to be the most suitable for geoengineering (Heckendorn et al., 2009).
The amount of injection, evolution of the size of the particles, and removal processes influence the radiative forcing and resulting climate change in state-of-the-art climate models that simulate the evolution and transport of sulfate aerosols. The rate of injection, location, and altitude of injection control processes such as particle growth (by nucleation, condensation, coagulation or evaporation), transport, and gravitational settling and removal processes (Heckendorn et al., 2009; Niemeier and Timmreck, 2015; Tilmes et al., 2017; Kleinschmitt et al., 2018), and strongly influence the efficiency of the stratospheric geoengineering schemes. The amount of cooling produced by continuous sulfate aerosol injection initially increases as the rate of injection increases but then decreases as the rate increases further (Niemeier et al., 2011; Niemeier and Timmreck, 2015; Kleinschmitt et al., 2018). This is because as the rate of injection increases beyond a threshold, coagulation increases, forming larger particles. Larger particles are less efficient at scattering sunlight and are more susceptible to removal through sedimentation (Tilmes et al., 2017; Kleinschmitt et al., 2018).
The altitude of injection affects the microphysics and transport of the aerosols in the stratosphere and thereby affects the amount of cooling produced. High-altitude injection of the aerosols extends the sedimentation time and contributes to a longer aerosol lifetime in the stratosphere (Heckendorn et al., 2009: Niemeier et al., 2011; Niemeier and Timmreck, 2015). Niemeier et al. (2013) found that the altitude of the of aerosol layer could affect the radiative transfer through the atmosphere: a reflecting layer in the lower altitude causes a smaller magnitude of top-of-the-atmosphere (TOA) SW forcing due to absorption and downward reflection of the upward beam. In the stratosphere, circulation patterns associated with the Brewer–Dobson circulation (BDC) are important as they influence aerosol transport and burden. Tilmes et al. (2017) show that, for equatorial high-altitude injections, total aerosol burden in the tropics increases more than for the low-altitude injections because aerosols are carried upward by the deep branch of the BDC in the tropics. For high-altitude injections outside the Equator, they find that the aerosols are transported more effectively toward middle and high latitudes by the deep branch of BDC. For the low-altitude injections, the aerosols remain in the shallow branch of the BDC and are removed rapidly from the stratosphere (Tilmes et al., 2017). The longer lifetime also leads to particles with larger effective radii that reduce the scattering effect and that sediment faster from the stratosphere. Kleinschmitt et al. (2018) find that for tropical injections the net radiative forcing is nearly independent of the altitude of injection despite an increase in the sedimentation time with the altitude of injection, due to the counteracting effects of the particle growth (and hence shorter lifetime) and the resulting reduced scattering properties.
The climates generated by stratospheric sulfate injections can be modulated by varying the timing, latitude, and altitude of aerosol injection. A set of studies using the Whole Atmosphere Community Climate Model (CESM1-WACCM) showed that multiple simultaneous climate objectives could be met by strategically injecting aerosols at multiple locations in the stratosphere (Tilmes et al., 2017, 2018a; Kravitz et al., 2017; MacMartin et al., 2017). These studies have shown that the spatial pattern of aerosol optical depth (AOD) can be partially controlled by optimizing the locations of injection (MacMartin et al., 2017; Kravitz et al., 2017). Non-equatorial high-altitude injections are more efficient at controlling the surface climate because the transport of aerosols into middle and high latitudes results in particles of a smaller effective radius and larger aerosol burden in these latitudes (Tilmes et al., 2017; MacMartin et al., 2017).
The studies discussed above have studied the climate responses mainly focused on the changes in aerosol burden with particle microphysics, transport, and removal processes. But there are several other fast-adjustment processes in the climate system which can impact effective radiative forcing and climate responses. Aerosols prescribed in the stratosphere can cause local warming in the stratosphere by absorbing near-IR and terrestrial radiation (Stenchikov et al., 1998; Ferraro et al., 2011). This warming can lead to changes in the amount of water vapor in the stratosphere (Dessler et al., 2013) and the amount of high clouds by changing the tropospheric stability (Kuebbeler et al., 2012; Visioni et al., 2018). Boucher et al. (2017) has shown that these fast adjustment processes can influence the effective radiative forcing of the climate system for sulfate aerosol injections. The altitude of the prescribed aerosol layer can thus affect the climate depending on the proximity of the heated layer to the tropopause as heat and mass exchange between the stratosphere and troposphere can lead to changes in clouds and stratospheric water vapor. Although most cited studies include the fast adjustment processes, and radiative forcing and response, there is a lack of clear and systematic understanding of the dependence of radiative forcing and climate response on the altitude of sulfate aerosols in the stratosphere.
In this study, we use idealized climate model experiments to systematically study the sensitivity of the effective radiative forcing and the simulated surface climate to the height at which aerosols are prescribed in the stratosphere. The models used in several previous studies include the effects of several processes that affect the aerosol microphysics, transport, and removal processes, and hence the altitude sensitivity estimated in these studies is the net effect of all these processes. The idealized prescribed aerosol model used in this study has the advantage of isolating and analyzing the individual effects, which will be challenging in complex models. In all our stratospheric aerosol experiments, we use the same total amount of aerosols but alter their altitude. Thus, our idealized simulations are intended to highlight the radiative influences of aerosol layer height and isolate these effects from effects associated with aerosol particle evolution and transport.
2.1 Model details
To study the dependence of the surface climate on the height of the sulfate aerosols in the stratosphere, we use the NCAR Community Earth System Model version 1.0.4 (CESM; Gent et al., 2011). The CESM consists of five components: atmosphere (Community Atmosphere Model version 4 – CAM4), sea ice (Community Ice Code version 4 – CICE4), land (Community Land Model version 4 – CLM4), ocean (Parallel Ocean Program – POP), and land ice (Community Ice Sheet Model), which are coupled through a coupler. For this study, we use a configuration where CAM4 is coupled with the Community Land Model and a slab ocean model (SOM) for simulating the climate change. We also use the prescribed sea surface temperature (pSST) configuration of CAM4 for estimating the radiative forcings. The configuration used here has a horizontal resolution of 1.9∘ in latitude and 2.5∘ in longitude, and a vertical resolution of 26 layers with 8 model layers in the stratosphere. The top of the atmosphere (TOA) in the model is approximately at 3 hPa. The land model used here, (CLM4) has an integrated representation of water, carbon, and nitrogen cycles (Oleson et al., 2010).
2.2 Experimental design
The reference climate of our study is based on a 100-year pre-industrial control simulation (called “1XCO2” hereafter) with the atmospheric CO2 concentration fixed at 284.7 ppm. We also perform a “2XCO2” experiment where the atmospheric CO2 concentration is doubled to 569.4 ppm. To assess the sensitivity to the altitude of the prescribed aerosols, a set of three stratospheric aerosol experiments are designed by altering the altitude of the additional aerosol layer but keeping the total mass of aerosols constant at 20 Tg and CO2 concentration at 569.4 ppm. The mass of aerosol was chosen based on Nalam et al. (2017), where they prescribed 20 Tg of background sulfate aerosols in five layers centered at 37 hPa to offset the global mean surface temperature change caused by a doubling of CO2. In CAM4, the sulfate aerosols are log-normally distributed with fixed size distributions (Neale et al., 2010). For our stratospheric aerosol experiments, we use volcanic aerosols which have an effective mean radius of 0.426 µm and a geometric standard deviation of 1.25. The mass of the aerosols consists of 75 % H2SO4 and 25 % H2O (Neale et al., 2010). The zonal variations as well as interannual variations (for this study) in mixing ratio of the volcanic aerosols are omitted (Ammann et al., 2003; Neale et al., 2010). The volcanic aerosol size used here corresponds to the large aerosols formed 6 to 12 months after a volcanic eruption (Stenchikov et al., 1998; Bauman et al., 2003; Rasch et al., 2008). The aerosols are prescribed as a globally uniform layer in the stratosphere as shown in Fig. 1. Processes such as aerosol microphysics, chemistry, transport, and sedimentation are not included, and the aerosol layer remains fixed throughout the simulations. The aerosols are distributed in single model layers centered at pressure levels 100, 70, and 37 hPa altitudes with layer thicknesses in the range of 15.5±1.0 hPa in each case. Corresponding standard atmospheric heights are approximately 16, 19, and 22 km. These experiments are referred to as Volc_100hPa, Volc_70hPa, and Volc_37hPa.
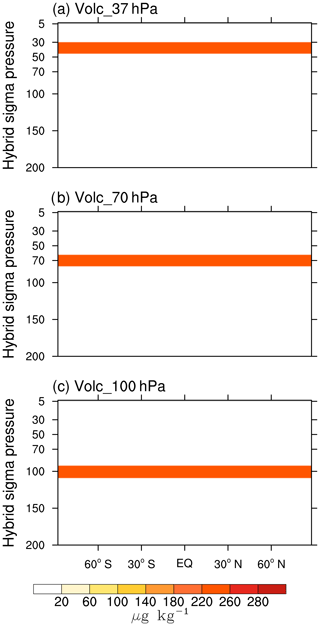
Figure 1Vertical distribution of the volcanic aerosols used in our stratospheric sulfate aerosol simulations. The aerosol layers are centered at (a) 37 hPa (b) 70 hPa, and (c) 100 hPa with a thickness of approximately 16 hPa.
In CAM4, the solar radiation is divided into 19 discrete spectral and pseudo-spectral intervals in the radiation module (Briegleb, 1992; Collins, 1998; Neale et al., 2010). The near IR absorption by volcanic aerosols is calculated in the model along with the long-wave (LW) absorption which is a function of the seven LW bands specified in the model. The concentration distributions of all other types of aerosols in the model such as dust, organic carbon, black carbon, and sea salt are unchanged in the 2XCO2 and in the three stratospheric aerosol experiments. All the slab ocean model simulations are performed for 100 years. Climate change analysis is performed on the last 60 years of model-generated data (from year 41 to 100), as the simulated climate closely approaches equilibrium within the first 20–30 years. The corresponding prescribed SST model configuration is used to simulate 60 years and the last 30 years of data are used for estimating radiative forcing and related fast adjustments.
Before discussing the main results, it is instructive to briefly review the concepts of effective radiative forcing, fast adjustments, efficacy of different forcing agents, and the efficiency of aerosols. These concepts are discussed briefly in the Supplement Sect. S1, where the various methods of estimating the effective radiative forcing are also discussed: the prescribed SST method (Hansen et al., 2005; Bala et al., 2010), the regression method (Gregory et al., 2004; Gregory and Webb, 2008), and the two-point method (Modak et al., 2018; Duan et al., 2018). The results on effective radiative forcing are presented in Sect. 3.1, and results for the climate feedback parameter and efficacy (Sect. S1) are presented in Sect. 3.2. Throughout Sect. 3, the uncertainties in the global mean values of the variables of any simulation are represented by 1 standard deviation to show the internal variability and the uncertainties for the changes are represented by standard error.
3.1 Global mean temperature and net top-of-atmosphere fluxes
Because our sulfate simulations produce cooling from a 2XCO2 background state, in the interest of consistency we report all results relative to the 2XCO2 simulation. The results for global mean temperature change and TOA fluxes are shown in Fig. 2 and Table 1. A halving of CO2 concentrations from the 2XCO2 state in the prescribed SST configuration causes a TOA net radiative flux (ΔNSST) of W m−2 at TOA (Fig. 2a), as found in previous studies that used the CAM4 model (Nalam et al., 2017). Due to land surface cooling, the global mean surface temperature change (ΔTSST) is K in this case. Quasi-steady-state results for halving of CO2 concentrations from the 2XCO2 state in the slab ocean model configuration show global mean temperature change (ΔTSOM) of K and TOA flux change (ΔNSOM) of W m−2 in this case.
Table 1Radiative forcing estimates and global annual mean temperature changes relative to the 2XCO2 case, and climate sensitivity and efficacy. Uncertainties for changes are estimated as 2 standard errors. Uncertainties are calculated from 60 annual mean differences for slab ocean and 30 annual means for prescribed SST experiments. The two-point method of estimating the radiative forcing, and climate sensitivity and efficacy are discussed in Sect. S1.

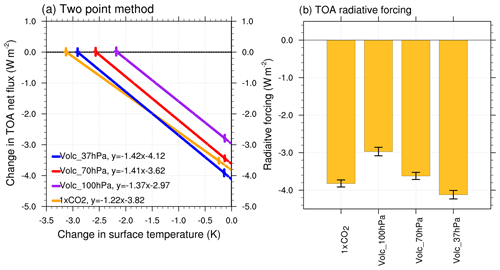
Figure 2(a) The two-point method for estimating radiative forcing and feedback parameter (Sect. S1). Change in global and annual mean surface temperature and TOA radiative imbalance from the slab ocean (points on the left) and prescribed SST (points on the right) simulations relative to the 2XCO2 simulation. The climate feedback parameter (slope of the lines) and the effective radiative forcing (intercept on the y axis on the right) for CO2 change (1XCO2–2XCO2) and all stratospheric sulfate experiments can be inferred from the linear regression relationships shown in the figure legends. Horizontal and vertical bars show 2 standard errors of the annual mean differences in surface temperature and radiative forcing relative to 2XCO2 experiment, respectively. The standard errors are estimated using 30 annual means for prescribed SST simulations and 60 annual means for slab ocean simulations. (b) The global annual mean TOA radiative forcing at top of the atmosphere relative to the 2XCO2 experiment, estimated using the two-point method as illustrated in panel (a). The error bars represent 2 standard errors calculated from 30 annual means of the difference from the 2XCO2 experiment.
There is more negative TOA radiative imbalance when the volcanic aerosols are prescribed at a higher altitude (Fig. 2a): ΔNSST is , , and W m−2, for the Volc_100hPa, Volc_70hPa, and Volc_37hPa prescribed SST simulations, respectively, relative to the 2XCO2 control case. The corresponding global mean surface temperature changes (ΔTSST) in these prescribed SST simulations are , , and , respectively. The TOA radiative imbalance discussed here are actually the prescribed SST radiative forcing as discussed in several previous studies (Bala et al., 2010; Modak et al., 2014; Nalam et al., 2017). This imbalance is corrected for the land surface temperature change in the prescribed SST simulations, to obtain the TOA radiative forcing (Sect. 3.2) in the two-point method as discussed in Modak et al. (2018) and Duan et al. (2018) and in Sect. S1. Residual TOA net fluxes in the steady state for the sulfate aerosol slab ocean simulations (ΔNSOM) are 0.02±0.13, 0.01±0.13, and 0.0±0.12, for the Volc_100hPa, Volc_70hPa, and Volc_37hPa simulations respectively. The corresponding ΔTSOM values are , , and K, respectively.
3.2 Radiative forcing and climate feedback parameters
With the values presented above, using Eqs. (1) and (2) in Sect. S1, we can calculate the effective radiative forcing (F) and climate feedback parameters (λ) for each of our experimental simulations (Fig. 2 and Table 1) using the two-point method (Sect. S1). A halving of CO2 concentration from 2XCO2 to 1XCO2 results in an estimate for F of W m−2, and an estimate for λ of 1.22±0.05 W m−2 K−1. Introduction of stratospheric aerosol layers at 100, 70, and 37 hPa results in estimates for F of , , and W m−2, respectively. Corresponding estimates of λ are 1.37±0.09, 1.41±0.07, and 1.42±0.06 W m−2 K−1. Thus, there is a substantial increase in the magnitude of radiative forcing from sulfate aerosols when they are higher in the stratosphere (Fig. 2b); this effect appears to be slightly offset by a small (i.e., not statistically significant) increase in the climate feedback parameter. For example, for the 37 hPa case relative to the 100 hPa case, the radiative forcing is 38 % larger in magnitude, but the climate feedback parameter is 3 % larger, resulting in a temperature change that is 34 % larger in magnitude. The climate feedback parameters for sulfate aerosols differs substantially from the climate feedback parameter for CO2, resulting in efficacy values (eSAI) of 0.89±0.07, 0.87±0.05, and 0.86±0.05 for the Volc_100hPa, Volc_70hPa, and Volc_37hPa cases, respectively, indicating that effective radiative forcing from stratospheric sulfate aerosols would generate 11 % to 14 % less global mean temperature change than would an equivalent amount of effective radiative forcing from CO2. Hence, the efficacy of sulfates is less than 1 as also found in recent studies (e.g., Duan et al., 2018), and for an equivalent amount of effective radiative forcing, CO2 reduction would be more effective in cooling the climate. The magnitude of climate feedback parameter differs slightly between the stratospheric sulfate experiments, which is mainly associated with the changes in the cloudy-sky feedback parameters (Fig. S1 in the Supplement). The reasons for these changes are not analyzed here but will be investigated in detail in a future study. The larger magnitude of the climate feedback parameter obtained for sulfate aerosols relative to the CO2 forcing is qualitatively similar to the difference between the feedback parameters for solar irradiance and CO2 forcing found in a recent study (Modak et al., 2016). Our calculated efficacy values for stratospheric sulfate aerosols are somewhat larger than the value of 0.83 for solar irradiance estimated by Modak et al. (2016). This is likely due to differing climate sensitivity of the version of the atmospheric model used (CAM5 in Modak et al., 2016 and CAM4 for our experiments) and the differing heating structures in the stratosphere for changes in solar irradiance versus sulfate aerosols. The efficacy value estimated for sulfates in our study is broadly consistent with that reported by Duan et al. (2018) where it is found that the efficacy of sulfate aerosols at the top of the atmosphere relative to CO2 is 0.85.
We have also applied the two-point method (Sect. S1) to the individual radiative forcing components. The radiative forcing and corresponding feedback parameters are shown in Fig. S1 and Table S1, which indicate that the LW forcing from volcanic aerosols are not negligible (Fig. 3b) – the magnitude is about 13 % of the SW forcing. The total LW radiative forcing is positive in the stratospheric aerosol experiments relative to the 2XCO2 case (i.e., increased downward LW radiation; Fig. 3b) but the negative SW forcing dominates (i.e., increased upward SW radiation; Fig. 3a), and hence the net TOA radiative forcing is negative relative (increased upward) to the 2XCO2 case (Fig. 2b). A detailed analysis of the radiative forcing components and fast adjustments in clouds, water vapor, and temperature are given below.
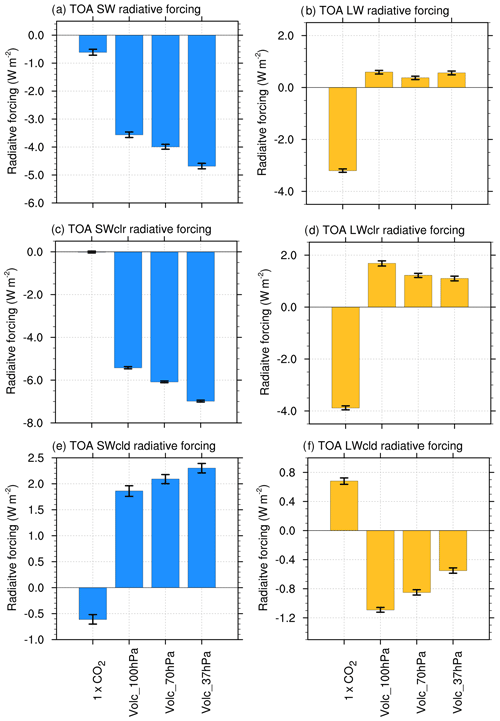
Figure 3TOA SW and LW radiative forcing for all-sky (a, b) clear-sky (c, d) and cloudy-sky (e, f) conditions relative to the 2XCO2 experiment, estimated using the two-point method (Sect. S1). The error bars represent 2 standard errors calculated from 30 annual means of the difference from the 2XCO2 experiment.
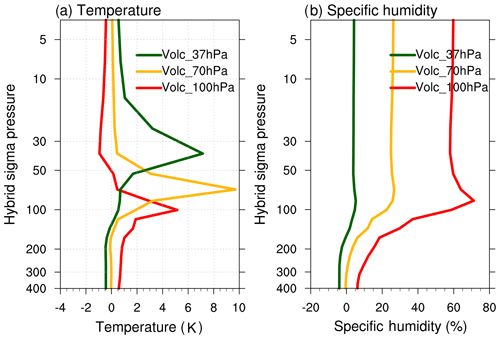
The clear-sky SW radiative forcing is negative in all cases (Fig. 3c) due to the SW backscattering by the prescribed aerosols. The sensitivity to the altitude of aerosols can be explained by the changes in water vapor content in the stratosphere. When aerosols are prescribed at lower levels close to the tropopause, radiative heating by aerosols leads to an increase in cold-point tropopause temperature and an increase in stratospheric water vapor (Fig. S2). The increase in water vapor leads to increased absorption of SW radiation, which can provide strong positive water vapor feedback. As the changes in water vapor amount decreases rapidly in the stratosphere with height of the prescribed aerosols, the water vapor feedback-related SW absorption decreases, and hence we find a larger negative SW clear-sky radiative forcing when aerosols are prescribed at higher altitudes (Fig. 3c).
The clear-sky LW forcing is positive for all cases (Fig. 3d) due to LW absorption by volcanic aerosols and their differences are associated with different changes in water vapor. As discussed earlier, there is an increase in water vapor (Fig. S2) which is larger when aerosols are prescribed at lower levels. As water vapor absorbs LW radiation, we find that the LW clear-sky forcing increases when aerosols are prescribed at lower stratospheric levels.
The SW cloud radiative forcing is positive in all cases (Fig. 3e) because of a reduction in clouds in the stratospheric aerosol experiments relative to the 2XCO2 case (Fig. S3a). The upper troposphere warms in the stratospheric aerosol experiments (Figs. S4 and S5) because of mixing between the tropospheric and radiatively heated stratospheric air. As the upper troposphere warms, the stability of the troposphere increases which causes a reduction in water vapor transport to the upper troposphere, the probability of ice supersaturation and a reduction of high clouds (Kuebbeler et al., 2012; Visioni et al., 2018). Similar to these studies, a reduction in high cloud cover is simulated in our stratospheric aerosol experiments relative to the 2XCO2 (Figs. S3b, S6). Further, the increase in stability and decrease in water vapor transport to the upper troposphere leads to a smaller decrease in the low cloud fraction for the Volc_100hPa case compared to the Vol_70hPa and Volc_35hPa cases (Fig. S3c). The increase in tropospheric stability is less when aerosols are prescribed at higher stratospheric levels as the upper tropospheric warming decreases. As low clouds are optically thicker than high clouds and their increase is larger for the Volc_100hPa case (Fig. S3c), a corresponding less positive SW cloud radiative forcing is simulated in the Volc_100hPa case (Fig. 3c).
A sensitivity of cloudy-sky LW forcing to the height of the aerosols is also simulated (Fig. 3f) which can be attributed to the changes in high cloud cover in the stratospheric aerosol experiments (Figs. S3b and S6). The decrease in high clouds results in a cirrus cloud thinning effect (Storelvmo et al., 2013) and allows more LW radiation to pass through the atmosphere resulting in negative LW forcing. The magnitude of this effect decreases as the aerosols are prescribed at higher altitudes (Fig. 3f). In the Vol_100hPa case, the magnitude of the cloud-induced LW forcing is about one-third of the net SW forcing which shows that the indirect high cloud effect is large.
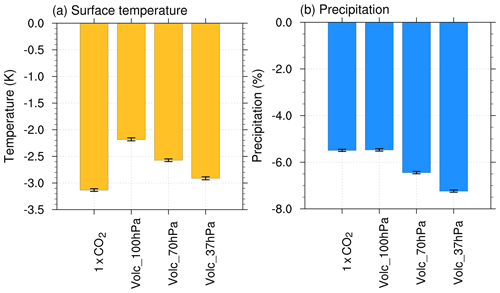
Figure 4Changes in global and annual mean (a) surface temperature and (b) precipitation relative to the 2XCO2 experiment (slab ocean simulations). The error bars represent 2 standard errors calculated from 60 annual means of the difference from the 2XCO2 experiment.
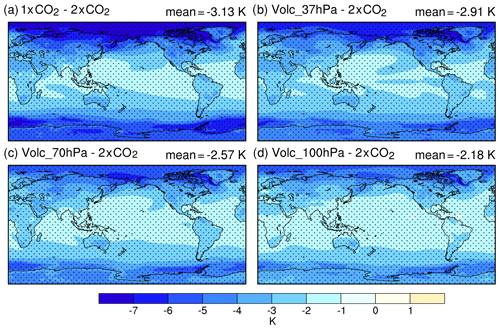
Figure 5The spatial pattern of changes in the surface temperature relative to the 2XCO2 experiment (slab ocean simulations). The hatched areas show the regions where the changes are significant at the 5 % significance level, and the changes are significant over the globe at this significance level in all experiments. The significance level is estimated using Student t test from 60 annual means of the experiments. Global mean value of the changes in each experiment is shown at the top right of each panel.
3.3 Global climate change
The radiative forcing of −3.82 W m−2 from a halving of CO2 in the 1XCO2 experiment leads to a decrease in global mean surface temperature by 3.13 K (Figs. 4a and 5a). In the stratospheric aerosol experiments, the aerosol-induced negative radiative forcing induces a surface cooling (Fig. 4a). As the TOA radiative forcing varies with the altitude of the aerosols in the stratospheric aerosol experiments, corresponding changes are simulated in surface temperature. Global cooling is greater when volcanic aerosols are prescribed at the higher levels of the stratosphere (Fig. 4a). The spatial changes in the global mean surface temperature for the stratospheric aerosol experiments relative to the 2XCO2 experiment are shown in Fig. 5. In all stratospheric sulfate experiments larger surface cooling is simulated in the higher latitudes compared with the tropics which is consistent with the polar amplification simulated for an increase in CO2 (Fig. S7a). Compared to other stratospheric sulfate experiments, the lower net negative radiative forcing in the Volc_100hPa case contributes to a global mean surface cooling of 2.18 K with respect to the 2XCO2 experiment, which attains only 70 % of the cooling in 1XCO2 relative to 2XCO2. For the Volc_70hPa case, the surface cooling increases to 2.57 K relative to the 2XCO2 case reaching 82 % of cooling due to halving of CO2. Larger negative forcing in the Volc_37hPa case compared to other cases leads to more surface cooling in Volc_37hPa and thereby attaining ∼93 % of the cooling simulated in the 1XCO2 case.
The residual surface temperature patterns in the stratospheric aerosol simulations relative to 1XCO2 experiment (Fig. S7) shows a large warming at the higher latitudes. This is in agreement with several previous studies (Govindasamy et al., 2003; Kravitz et al., 2016; Nalam et al., 2017). The net surface cooling in the Volc_37hPa is less than the 1XCO2 experiment even-though the net negative radiative forcing surpasses the 1XCO2 radiative forcing (Figs. 2b and 4a). This is partly attributed to the lower efficacy of sulfate aerosol forcing (0.86–0.89; Sect. 3.2) and partly to the CO2 physiological effect. For counteracting the global mean surface warming, the magnitude of sulfate forcing should be larger than CO2 radiative forcing as its efficacy is less than 1. The lower efficacy of sulfate aerosols is similar to the case of solar forcing, which has an efficacy of about 0.8 (Schmidt et al., 2012; Modak et al., 2016; Duan et al., 2018). The CO2 physiological forcing is caused by elevated CO2 concentration, where the plant stoma opens less widely, leading to less canopy transpiration and reduced evapotranspiration which leads to an increase in mean surface air temperature over land (Cao et al., 2010).
Kravitz et al. (2013a) have shown that for an abrupt increase in CO2 concentration, the precipitation initially reduces due to the fast adjustment to CO2 forcing, and later increases in response to the temperature increase. Fast adjustments to CO2 radiative forcing results in precipitation suppression (Bala et al., 2010; Ferraro et al., 2014), associated with an increase in stability in the lower troposphere (Bala et al., 2010; Cao et al., 2012). The fast precipitation change is related to atmospheric radiative imbalance (Liepert and Previdi, 2009) and is also associated with reduced evaporation (Kravitz et al., 2013a). Thus, the fast response to a reduction in CO2 radiative forcing involves an increase in precipitation. In contrast, the fast response to the negative forcing from the introduction of a stratospheric aerosol layer does not involve an increase in global mean precipitation. The surface cooling caused by a halving of CO2 in the 1XCO2 experiment is associated with a decrease in global mean precipitation and the net change is −5.8 % relative to the 2XCO2 experiment (Figs. 4b and 6a). In the stratospheric aerosol experiments, even though the global mean surface cooling is less than in the 1XCO2 experiment, a larger net reduction in global mean precipitation is simulated because the introduction of a stratospheric aerosol layer does not lead to an increase in fast global mean precipitation. For all types of forcing considered here, a decrease in global mean temperatures is associated with decreases in global mean precipitation. For our volcanic aerosol simulations, both equilibrium global mean surface temperatures and equilibrium global mean precipitation decrease with increasing altitude of the stratospheric aerosol layer (Fig. 4b). The spatial patterns (Fig. 6) show that the reduction in precipitation is larger over the tropics which is consistent with earlier studies (Govindasamy et al., 2003; Kravitz et al., 2013b; Tilmes et al., 2013).

Figure 6The spatial pattern of changes in precipitation relative to the 2XCO2 experiment (slab ocean simulations). The hatched areas show the regions where the changes are significant at the 5 % significance level. The significance level is estimated using Student t test from 60 annual means of the experiments. Global mean value of the changes in each experiment is shown at the top right of each panel.
3.4 Stratospheric dynamics
An increase in the atmospheric CO2 concentration causes a warming of the surface and the troposphere but a cooling in the stratosphere and mesosphere (Goessling and Bathiany, 2016, and references therein). Additionally, the local warming by aerosols can affect the dynamics of the stratosphere (Aquila et al., 2014; Niemeier and Schmidt, 2017). The vertical resolution of the model is likely to be inadequate for simulating the complex stratospheric dynamics and features such as quasi-biennial oscillation (QBO), which require “high-top” versions of CAM such as Whole Atmosphere Community Climate Model (WACCM; Marsh et al., 2013; Tilmes et al., 2017; Mills et al., 2017) that has high vertical resolution in the stratosphere. However, some recent studies have shown that even with limited vertical resolution, the CAM4 model is capable of simulating stratospheric circulation patterns such as the BDC (e.g., Smith et al., 2015; Tilmes et al., 2015), which is important for vertical and meridional water vapor transport in the stratosphere.
We have performed a set of additional, 12-member ensemble simulations lasting 1 d to evaluate the effects of aerosols on the radiative heating. These 1 d runs provide an estimate of the instantaneous radiative effects of the prescribed aerosols. Monthly restarts from the 60th year of the prescribed SST control run are used to initialize these 1 d runs. Each member of the ensemble starts from the first day of each calendar month (1 January, 1 February, …) and the simulation is performed with hourly outputs from the model. By averaging the 12 ensemble runs, the effects of seasonal cycle on the radiative forcing estimates are excluded.
The SW heating rate increases with the prescribed altitude, with a maximum warming of 0.24 K d−1 for Volc_100hPa to 0.39 K d−1 for Volc_70hPa, and 0.43 K d−1 for Volc_37hPa (Fig. S8a). This is because the amount of solar radiation decreases downward due to attenuation and hence more SW radiation is available at higher altitudes. For LW heating, a maximum of 0.32 K d−1 is simulated for the Volc_70hPa case, while the maximum is 0.13 K d−1 for the Volc_100hPa case, and 0.16 K d−1 for the Volc_37hPa (Fig. S8b). We are not aware of the reason for the maximum LW heating in the Volc_70hPa. Due to the differing SW and LW radiative heating rates in the three cases, the maximum heating rate and temperature change are simulated for the Volc_70hPa case (0.68 K d−1), followed by Volc_37hPa (0.58 K d−1) and Volc_100hPa (0.34 K d−1; Fig. S8c).
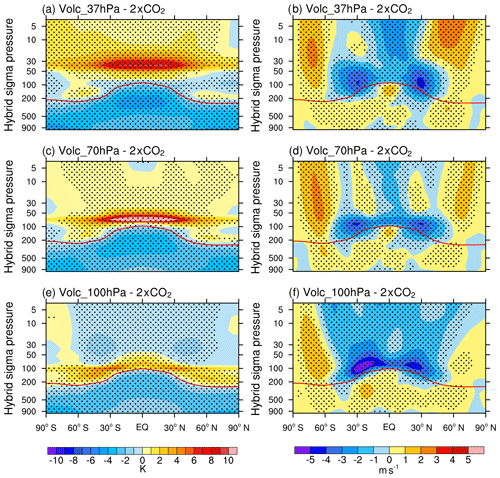
Figure 7The changes in zonal average temperature (a, c, e) and winds (b, d, f) in the three stratospheric sulfate simulations (slab ocean simulations) relative to the 2XCO2 simulation. Position of the tropopause in each case is marked as a red line. The hatched areas in the plot show the regions where the changes are significant at the 5 % significance level. The significance level is estimated using Student t test from 60 annual means of the experiments.
To illustrate the effects of aerosol-induced warming on the dynamics of the stratosphere, changes in zonal mean temperature and wind for the stratospheric aerosol experiments with respect to the 2XCO2 simulation are analyzed (Fig. 7). Although the aerosols are prescribed uniformly around the globe, for the same altitude more warming is simulated in the tropics than in the poles (Fig. 7a) because the annual mean incoming solar radiation is larger in the tropics, and hence the aerosol-induced warming is larger in the tropics. A maximum warming of approximately 6 K is simulated for the Volc_100hPa case relative to the 2XCO2 experiment. The maximum warming increases to almost 15 K for the Volc_70hPa case and it is approximately 10 K for the Volc_37hPa case. The uneven meridional distribution of radiative heating (Fig. 7) alters the thermal wind balance in the stratosphere, resulting in high-latitude westerly wind anomalies (Ferraro et al., 2015) and low-latitude easterly anomalies. Large westerly wind anomalies are simulated for the Volc_70hPa and Volc_37hPa cases (Fig. 7b, d) as the radiative heating is larger in these two cases (Fig. S8). In models which simulate QBO, sulfate injection could lead to prolonged westerly phase of QBO in the tropical lower stratosphere (Aquila et al., 2014). Since the model used in this study does not simulate QBO, in the tropics, easterly wind anomalies are simulated in all cases with maximum magnitude in the Volc_100hPa case (Fig. 7).
The radiative heating by sulfate aerosols, especially in the lower stratosphere leads to an increase in temperature of the tropical tropopause layer and an associated increase in water vapor transport from the troposphere to the stratosphere (Dessler et al., 2013). When the volcanic aerosols are prescribed at 100 hPa, the warming is near the tropical tropopause and it causes a significant increase in water vapor in the stratosphere (Fig. 8). An increase in specific humidity of 60 % is simulated in the stratosphere for the Volc_100hPa case relative to the 2XCO2 experiment (Fig. 8). Though the radiative heating is largest for the Volc_70hPa experiment, the altitude of the layer is much above the tropopause and thus only a 25 % increase in specific humidity is simulated. No significant changes in specific humidity are simulated for Volc_37hPa case.
3.5 Effects on terrestrial vegetation productivity
The vegetation primary productivity on land is proportional to the available photosynthetically active radiation at the surface (Pinker and Laszlo, 1992), which is the sum of direct and diffuse solar radiation (Alados and Alados-Arboledas, 1999). In our stratospheric aerosol experiments, a reduction in direct solar radiation reaching the surface is simulated due to the increased SW scattering by the aerosols (Fig. S9, Table 2). However, the diffuse solar radiation reaching the surface increases (Fig. S9b; Kalidindi et al., 2015). This causes a diffuse fertilization effect, where the increase in diffuse radiation leads to increased productivity by increasing the light availability to a larger fraction of the canopy which otherwise remains shaded (Mercado et al., 2009; Kanniah et al., 2012). Thus, diffuse radiation can cause an increase in productivity and can enhance the terrestrial carbon uptake (Alton et al., 2007; Mercado et al., 2009). Increased diffuse radiation availability and suppressed plant and soil respiration due to cooling can enhance the terrestrial carbon sink in a sulfate geoengineering scenario (Xia et al., 2016).
Table 2Global and annual mean values of key land model variables from the 1XCO2 and 2XCO2 simulations and the change in these variables in the stratospheric sulfate experiments relative to the 2XCO2 experiment. Uncertainties for changes are estimated as 2 standard errors calculated from 60 annual mean differences. Uncertainties for 1XCO2 and 2XCO2 cases are estimated as the standard deviation from the 60 annual means. Percentage changes from the 2XCO2 simulation is given in parenthesis.
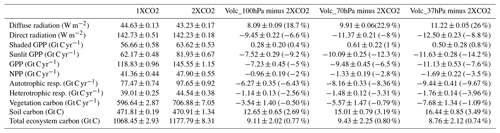
The changes in the global mean values over land for the diffused and direct solar radiation components and corresponding changes in primary productivity for the experiments with respect to the 2XCO2 case are shown in Table 2. In the 2XCO2 experiment, there is an increase of 26.72 Gt C yr−1 (22.5 %) in gross primary productivity (GPP) compared to the 1XCO2 experiment although the amount of radiation available for productivity is approximately the same in both cases. A doubling of CO2 concentration causes an increase in the plant productivity due to the CO2 fertilization effect (Farquhar, 1997; Owensby et al., 1999). To exclude the CO2 fertilization effect and assess the changes due to only the prescribed aerosols in the stratospheric aerosol experiments, changes in radiation and productivity are discussed relative to the 2XCO2 experiment below.
For the Volc_100hPa case, a decrease of 9.5 W m−2 (−6.64 %) in direct radiation relative to the 2XCO2 case is simulated. The reduction in direct radiation increases with the altitude of aerosols to −11.4 W m−2 (−8 %) and −12.5 W m−2 (−8.8 %) for the Volc_70hPa, and Volc_37hPa cases, respectively. An increase in diffuse radiation of 8.1 W m−2 is simulated for the Volc_100hPa case, which is 18.7 % larger than in the 2XCO2 case. As the height of volcanic aerosol increases, the increase in diffuse radiation at the surface becomes larger and the increase reaches 26 % (11.2 W m−2) of the 2XCO2 case for the Volc_37hPa case. The changes simulated in the diffuse radiation and direct radiation are of a similar magnitude in all sulfate aerosol experiments. Thus, the decrease in the direct radiation is partially offset by the increase in availability of diffuse radiation at the surface. From Table 2, it can be inferred that the net reduction in solar radiation at the surface is about 1.3 W m−2 (∼0.7 %).
Spatial patterns of direct and diffuse radiation change relative to the 2XCO2 experiment for the Volc_100hPa case over the land shows that overall there is a decrease in direct radiation and an increase in diffuse radiation all over the globe (Fig. S9a, b). We found that these patterns are similar for the other two stratospheric sulfate experiments. Large changes in direct and diffuse radiation are simulated in the dry regions and deserts. Spatial pattern of vertically integrated cloud cover in the 2XCO2 case (Fig. S9c) show that these large changes in direct and diffuse solar radiation occur in areas where the total cloudiness is small.
The total GPP is the sum of sunlit GPP (which depends on direct solar radiation) and shaded GPP (which depends on diffuse solar radiation). The changes in total GPP in all cases are dominated by the change in the sunlit GPP (Table 2). Although the changes in direct and diffuse radiation are of comparatively similar magnitudes, the decrease in the sunlit GPP is significantly more (by an order of magnitude) than the increase in the shaded GPP (Table 2). Thus, the additional productivity due to the increased diffused radiation availability is overwhelmed by the reduction in the sunlit GPP. Other studies have also found that the effect from reduced direct radiation dominates the effect of increased diffuse radiation, and thus the net effect of sulfate geoengineering is to reduce plant productivity (e.g., Kalidindi et al., 2015).
The decrease in the sunlit GPP is less when volcanic aerosols are prescribed at the lower levels of the stratosphere as the reduction in direct sunlight at the surface is less. The changes in GPP can also be modulated by the availability of nitrogen as simulated by the CN (carbon and nitrogen) module in CLM4. When aerosols are prescribed at lower levels, there is less cooling which causes relatively more mineralization reducing the nitrogen limitation effect (Rustad et al., 2001). The net primary productivity (NPP) shows similar changes (Table 2): the minimum decrease in NPP is simulated in the Volc_100hPa case (−0.96 Gt C yr−1 relative to the 2XCO2 case). The percentage decrease in NPP (2.0 % to 3.5 %) is smaller than GPP (5.0 % to 7.6 %) because of a decrease in autotrophic respiration in the stratospheric aerosol experiments (NPP equals GPP minus autotrophic respiration; Table 2). The decrease in autotrophic and heterotrophic respiration is related to a relatively cooler climate in the stratospheric aerosol experiments compared to the 2XCO2 case.
Sensitivity of radiative forcing and surface temperature to the altitude of volcanic size sulfate aerosols in the stratosphere is analyzed in this study using a climate model with prescribed aerosol distributions. The model used is less comprehensive than models which simulate the aerosol microphysics, transport, and removal processes. By excluding these processes, we isolate the dependence of radiative forcing on the height of the aerosol layer. The sensitivity experiments are performed by prescribing aerosols of a size characteristic of volcanoes at three different altitudes in the stratosphere (100, 70, and 37 hPa) but keeping the total mass of the volcanic aerosols constant at 20 Tg (15 Tg of H2SO4).
We show that for the same additional aerosol mass, volcanic aerosols produce more negative radiative forcing when they are prescribed at higher altitudes in the stratosphere (Fig. 2b). The aerosol microphysical changes can affect the optical and radiative properties of the aerosols through nucleation, condensation, coagulation, hygroscopic growth, etc. (e.g., Heckendorn et al., 2009). The changes in the optical and radiative properties affect radiative forcing, and thereby influence surface cooling efficiency in the aerosol geoengineering schemes. Since microphysical or transport processes are not included in this study, the global mean surface temperature change is solely dependent on the effective radiative forcing, which is sensitive to the prescribed altitude of aerosols. The radiative heating by volcanic aerosol in the lower stratosphere leads to increased stability of the upper troposphere and a reduction in the high cloud cover, and increased water vapor transport to the stratosphere (Kuebbeler et al., 2012; Figs. S6, S2). However, the resulting negative LW forcing from cloud cover change is overwhelmed by the large positive LW forcing due to the absorption of radiation by prescribed aerosols (Fig. 3d, f). The high cloud changes are sensitive to the proximity of the heated layer to the tropopause and is thus sensitive to the altitude of the aerosols. The changes in tropospheric stability also contribute to changes in low cloud cover (Fig. S3). Further, the changes in tropopause cold-point temperature due to the radiative warming of the lower stratosphere and increased stratospheric humidity affect the clear-sky radiative forcing. The positive LW forcing offsets a part of the negative SW forcing in the stratospheric aerosol experiments. Thus, as shown in several previous studies such as Kleinschmitt et al. (2018), our study also highlights the importance of LW forcing in the efficiency of the stratospheric aerosol experiments. The LW forcing depends on the model, and several other factors such as the type of aerosol used, location of injection, stratospheric humidity, etc.
The differences simulated in radiative forcing are reflected in the surface temperature response and we find that volcanic aerosols cause more surface cooling when they are prescribed at higher levels of the stratosphere. Assuming a lifetime of 1 year of the aerosols in the stratosphere, the 20 Tg of aerosol used in this study is equivalent to 9.79 Tg yr−1 SO2 injection (or 4.9 Tg S yr−1). As this amount at 37 hPa almost completely attains the halving of CO2-induced cooling, the efficiency in cooling the surface is estimated as 0.59 K Tg S−1. The corresponding efficiencies for the Volc_70hPa and Volc_100hPa simulations are 0.52 and 0.44 K Tg S−1, respectively. The surface temperature difference between our stratospheric aerosol experiments shows that even when the processes such as aerosol microphysics, transport, and sedimentation are excluded, the differences in effective radiative forcing between the stratospheric aerosol simulations experiments is substantial.
For 6 Tg SO2 yr−1 injections, Tilmes et al. (2017) estimated a cooling of ∼0.22 K Tg S−1 for equatorial high-altitude injections (30 hPa) and ∼0.18 K Tg S−1 for equatorial low-altitude injections (60 hPa) when aerosols concentrations in the stratosphere had reached a steady state. While our results agree in sign, it should be noted that while Tilmes et al. (2017) estimated efficiency from experiments with sulfur emissions we have made estimates using a prescribed aerosol burden. Further, the surface cooling discussed in Tilmes et al. (2017) is from 10-year coupled simulations where the climate system has not reached a steady state, while our results are from equilibrium simulations. Further differences can be attributed to differing model configurations (slab ocean versus fully coupled) and different versions of the model used in the two studies.
With the surface cooling in stratosphere aerosol experiments, a reduction in global mean precipitation is simulated in the stratospheric aerosol experiments as shown in several previous studies (Bala et al., 2010; Modak and Bala, 2014; Nalam et al., 2017). The reduction in global annual mean precipitation increases as the height of the aerosol layer increases. Because of the absorption of radiation by volcanic aerosols, a significant warming in the stratosphere is simulated as reported in many previous studies (Ferraro et al., 2011; Niemeier and Schmidt, 2017; Richter et al., 2017). The magnitude of radiative warming is also sensitive to the altitude of the aerosols and a maximum warming of 15 K is simulated relative to the 2XCO2 experiment for the case where aerosols are prescribed at 70 hPa. The maximum warming simulated here is comparable to the maximum warming of 10 to 15 K simulated in other studies such as Richter et al. (2017) and Tilmes et al. (2018b). The aerosol-induced stratospheric warming and the resulting strong stratospheric high-latitude westerly and tropical easterly wind anomalies are sensitive to the altitude of the aerosols. Further, the radiative heating in the lower stratosphere causes the tropical upper tropopause layer to warm, which leads to increased water vapor transport into the stratosphere. In the stratospheric aerosol experiments, due to SW scattering by aerosols, there is an increase in diffused solar radiation and a decrease in direct solar radiation reaching the surface. Correspondingly, an increase in the shaded GPP and a decrease in the sunlit GPP are simulated. The net result is a decrease in GPP in all cases as the decrease in the sunlit GPP is significantly larger compared to the increase in the shaded GPP.
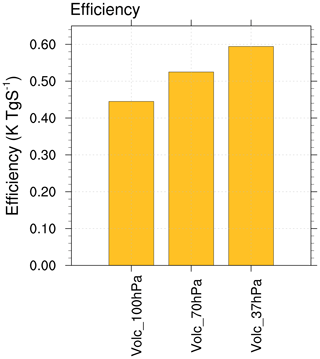
Figure 9Change in global mean surface temperature per Tg S in the stratosphere (efficiency) in the volcanic aerosol simulations.
There are several limitations to this study. First, the aerosols are distributed uniformly at specific heights with fixed particle size distributions in our simulations, which is likely not achievable in an actual stratospheric sulfate deployment scenario. Unlike the aerosol injection simulations, the sedimentation and vertical spread of the aerosols are not modeled in our study, and thus our idealized aerosol profile differs from the simulations that include sedimentation. Thus, the vertical spread of the aerosol-induced warming is not accounted for in our study which will have effects on the vertical structure of temperature and humidity changes, and magnitude of the fast adjustment processes mentioned in the study. A realistic prescribed distribution would be one that is calculated from an aerosol microphysical model. However, we believe that the qualitative and fundamental results obtained in this study will not be altered with a more realistic distribution. We intend to use a more realistic distribution of aerosols and repeat this sensitivity analysis in a future study.
Our experiments do not include the effects of particle growth, aerosol chemistry, transport, or its removal processes. The volcanic aerosol geometric mean radius used here (0.423 µm) is very close to the size where significant sedimentation can occur (Tilmes and Mills, 2014). A lack of ozone chemistry in the model and the absence of events such as internally generated QBO limits detailed analysis of stratospheric responses to the radiative warming by aerosols (Aquila et al., 2014; Kleinschmitt et al., 2018). For computational efficiency, we have used slab ocean version of the coupled model instead of fully dynamic ocean component and hence the transient effects and deep ocean feedback are missing in our study. Despite these limitations, we believe that our conclusions on the dependence of the radiative forcing and hence the surface climate on the altitude of the aerosol layer are more fundamental, and the robustness of our results should be assessed using multiple models in a future study.
To summarize, for the same mass, the efficiency (defined as changes in surface temperature per Tg S) of volcanic aerosol is less when it is prescribed at lower altitudes in the stratosphere (Fig. 9). For example, in our simulations, there is a surface cooling of 0.44 K for each teragram of sulfur placed in the stratosphere at about 16 km altitude (100 hPa). There is an additional surface cooling of 0.15 K per Tg S when the prescribed altitude is increased from about 16 km to about 22 km (37 hPa).
Model outputs and analysis scripts are available on request from the corresponding author.
The supplement related to this article is available online at: https://doi.org/10.5194/esd-10-885-2019-supplement.
KPSPK and GB designed the study, analyzed the data and wrote the manuscript. LC, LD, and KC contributed to the study design and writing of the manuscript.
Author Govindasamy Bala is a member of the editorial board of the journal. Other authors declare that they have no conflict of interest.
This work was funded by the Department of Science and Technology (DST), India grant no. DST/CCP/MRDP/96/2017(G). Numerical simulations were performed on the supercomputer SahasraT at the Supercomputer Education and Research Centre (SERC), Indian Institute of Science, Bengaluru. The authors thank Angshuman Modak (Indian Institute of Science) and Adithya Nalam (Institute for Advanced Sustainability Studies Potsdam) for their technical help.
This research has been supported by the Department of Science and Technology (DST), India (grant no. DST/CCP/MRDP/96/2017(G)).
This paper was edited by Axel Kleidon and reviewed by three anonymous referees.
Alados, I. and Alados-Arboledas, L.: Direct and diffuse photosynthetically active radiation: Measurements and modeling, Agr. Forest Meteorol., 93, 27–38, https://doi.org/10.1016/S0168-1923(98)00107-5, 1999.
Alton, P. B., North, P. R., and Los, S. O.: The impact of diffuse sunlight on canopy light-use efficiency, gross photosynthetic product and net ecosystem exchange in three forest biomes, Glob. Change Biol., 13, 776–787, https://doi.org/10.1111/j.1365-2486.2007.01316.x, 2007.
Ammann, C. M., Meehl, G. A., Washington, W. M., and Zender, C. S.: A monthly and latitudinally varying volcanic forcing dataset in simulations of 20th century climate, Geophys. Res. Lett., 30, 1657, https://doi.org/10.1029/2003GL016875, 2003.
Aquila, V., Garfinkel, C. I., Newman, P. A., Oman, L. D., and Waugh, D. W.: Modifications of the quasi-biennial oscillation by a geoengineering perturbation of the stratospheric aerosol layer, Geophys. Res. Lett., 41, 1738–1744, https://doi.org/10.1002/2013GL058818, 2014.
Bala, G., Caldeira, K., and Nemani, R.: Fast versus slow response in climate change: implications for the global hydrological cycle, Clim. Dynam., 35, 423–434, https://doi.org/10.1007/s00382-009-0583-y, 2010.
Bauman, J. J., Russell, P. B., Geller, M. A., and Hamill, P.: A stratospheric aerosol climatology from SAGE II and CLAES measurements: 2. Results and comparisons, 1984–1999, J. Geophys. Res., 108, 4383, https://doi.org/10.1029/2002JD002993, 2003.
Boucher, O., Kleinschmitt, C., and Myhre, G.: Quasi-additivity of the radiative effects of marine cloud brightening and stratospheric sulfate aerosol injection, Geophys. Res. Lett., 44, 11158–11165, https://doi.org/10.1002/2017GL074647, 2017.
Briegleb, B. P.: Delta-Eddington approximation for solar radiation in the NCAR Community Climate Model, J. Geophys. Res., 97, 7603–7612, https://doi.org/10.1029/92JD00291, 1992.
Budyko, M. I. (Eds): Climatic Changes. American Geophysical Union, Washington DC, https://doi.org/10.1029/SP010, 1977.
Cao, L., Bala, G., Caldeira, K., Nemani, R., and Ban-Weiss, G.: Importance of carbon dioxide physiological forcing to future climate change, P. Natl. Acad. Sci. USA, 107, 9513–9518, https://doi.org/10.1073/pnas.0913000107, 2010.
Cao, L., Bala, G., and Caldeira, K.: Climate response to changes in atmospheric carbon dioxide and solar irradiance on the time scale of days to weeks, Environ. Res. Lett., 7, 034015, https://doi.org/10.1088/1748-9326/7/3/034015, 2012.
Collins, W. D.: A global signature of enhanced shortwave absorption by clouds, J. Geophys. Res., 103, 31669–31679. https://doi.org/10.1029/1998JD200022, 1998.
Crutzen, P. J.: Albedo enhancement by stratospheric sulfur injections: a contribution to resolve a policy dilemma?, Climatic Change, 77, 211–219, https://doi.org/10.1007/s10584-006-9101-y, 2006.
Dai, Z., Weisenstein, D. K., and Keith, D. W.: Tailoring meridional and seasonal radiative forcing by sulfate aerosol solar geoengineering, Geophys. Res. Lett., 45, 1030–1039, https://doi.org/10.1002/2017GL076472, 2018.
Dessler, A. E., Schoeberl, M. R., Wang, T., Davis, S. M., and Rosenlof, K. H.: Stratospheric water vapor feedback. P. Natl. Acad. Sci. USA, 110, 18087–18091, https://doi.org/10.1073/pnas.1310344110, 2013.
Duan, L., Cao, L., Bala, G., and Caldeira, K.: Comparison of the fast and slow climate response to three radiation management geoengineering schemes, J. Geophys. Res.-Atmos., 123, 11980–12001, https://doi.org/10.1029/2018JD029034, 2018.
Farquhar, G. D.: Carbon dioxide and vegetation, Science, 278, 1411, https://doi.org/10.1126/science.278.5342.1411, 1997.
Ferraro, A. J., Highwood, E. J., and Charlton-Perez, A. J.: Stratospheric heating by potential geoengineering aerosols, Geophys. Res. Lett., 38, L24706, https://doi.org/10.1029/2011GL049761, 2011.
Ferraro, A. J., Highwood, E. J., and Charlton-Perez, A. J.: Weakened tropical circulation and reduced precipitation in response to geoengineering, Environ. Res. Lett., 9, 014001, https://doi.org/10.1088/1748-9326/9/1/014001, 2014.
Ferraro, A. J., Charlton-Perez, A. J., and Highwood, E. J.: Stratospheric dynamics and midlatitude jets under geoengineering with space mirrors and sulfate and titania aerosols, J. Geophys. Res.-Atmos., 120, 414–429, https://doi.org/10.1002/2014JD022734, 2015.
Gent, P. R., Danabasoglu, G., Donner, L. J., Holland, M. M., Hunke, E. C., Jayne, S. R., Lawrence, D. M., Neale, R. B., Rasch, P. J., Vertenstein, M., Worley, P. H., Yang, Z.-L., and Zhang, M.: The community climate system model version 4, J. Climate, 24, 4973–4991, 2011.
Goessling, H. F. and Bathiany, S.: Why CO2 cools the middle atmosphere – a consolidating model perspective, Earth Syst. Dynam., 7, 697–715, https://doi.org/10.5194/esd-7-697-2016, 2016.
Govindasamy, B., Caldeira, K., and Duffy, P. B.: Geoengineering earth's radiation balance to mitigate climate change from a quadrupling of CO2, Global Planet. Change, 37, 157–168, https://doi.org/10.1016/S0921-8181(02)00195-9, 2003.
Gregory, J. M. and Webb, M. J.: Tropospheric adjustment induces a cloud component in CO2 forcing, J. Climate, 21, 58–71, https://doi.org/10.1175/2007JCLI1834.1, 2008.
Gregory, J. M., Ingram, W. J., Palmer, M. A., Jones, G. S., Stott, P. A., Thorpe, R. B., Lowe, J. A., Johns, T. C., and Williams, K. D.: A new method for diagnosing radiative forcing and climate sensitivity, Geophys. Res. Lett., 31, L03205, https://doi.org/10.1029/2003GL018747, 2004.
Hansen, J., Lacis, A., Ruedy, R., and Sato, M.: Potential climate impact of the Mount Pinatubo eruption, Geophys. Res. Lett., 19, 215–218, https://doi.org/10.1029/91GL02788, 1992.
Hansen, J., Sato, M., Ruedy, R., Nazarenko, L., Lacis, A., Schmidt, G. A., Russell, G., Aleinov, I., Bauer, M., Bauer, S., Bell, N., Cairns, B., Canuto, V., Chandler, M., Cheng, Y., Del Genio, A., Faluvegi, G., Fleming, E., Friend, A., Hall, T., Jackman, C., Kelley, M., Kiang, N., Koch, D., Lean, J., Lerner, J., Lo, K., Menon, S., Miller, R., Minnis, P., Novakov, T., Oinas, V., Perlwitz, J., Perlwitz, J., Rind, D., Romanou, A., Shindell, D., Stone, P., Sun, S., Tausnev, N., Thresher, D., Wielicki, B., Wong, T., Yao, M., and Zhang, S.: Efficacy of climate forcings, J. Geophys. Res.-Atmos., 110, D18104, https://doi.org/10.1029/2005JD005776, 2005.
Heckendorn, P., Weisenstein, D., Fueglistaler, S., Luo, B. P., Rozanov, E., Schraner, M., Thomason, L. W., and Peter, T.: The impact of geoengineering aerosols on stratospheric temperature and ozone, Environ. Res. Lett., 4, 045108, https://doi.org/10.1088/1748-9326/4/4/045108, 2009.
IPCC: Contribution of Working Group I to the fifth assessment report of the intergovernmental panel on climate change, in: Climate change 2013: the physical science basis, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, UK and New York, NY, USA, 2013.
Kalidindi, S., Bala, G., Modak, A., and Caldeira, K.: Modeling of solar radiation management: a comparison of simulations using reduced solar constant and stratospheric sulfate aerosols, Clim. Dynam., 44, 2909–2925, https://doi.org/10.1007/s00382-014-2240-3, 2015.
Kanniah, K. D., Beringer, J., North, P., and Hutley, L.: Control of atmospheric particles on diffuse radiation and terrestrial plant productivity: A review, Prog. Phys. Geogr., 36, 209–237, https://doi.org/10.1177/0309133311434244, 2012.
Kleinschmitt, C., Boucher, O., and Platt, U.: Sensitivity of the radiative forcing by stratospheric sulfur geoengineering to the amount and strategy of the SO2 injection studied with the LMDZ-S3A model, Atmos. Chem. Phys., 18, 2769–2786, https://doi.org/10.5194/acp-18-2769-2018, 2018.
Kravitz, B., Rasch, P. J., Forster, P. M., Andrews, T., Cole, J. N. S., Irvine, P. J., Ji, D., Kristjánsson, J. E., Moore, J. C., Muri, H., Niemeier, U., Robock, A., Singh, B., Tilmes, S., Watanabe, S., and Yoon, J. H.: An energetic perspective on hydrological cycle changes in the Geoengineering Model Intercomparison Project, J. Geophys. Res.-Atmos., 118, 13087–13102, https://doi.org/10.1002/2013JD020502, 2013a.
Kravitz, B., Caldeira, K., Boucher, O., Robock, A., Rasch, P. J., Alterskjær, K., Karam, D. B., Cole, J. N. S., Curry, C. L., Haywood, J. M., Irvine, P. J., Ji, D., Jones, A., Kristjánsson, J. E., Lunt, D. J., Moore, J. C., Niemeier, U., Schmidt, H., Schulz, M., Singh, B., Tilmes, S., Watanabe, S., Yang, S., and Yoon, J.: Climate model response from the geoengineering model intercomparison project (GeoMIP), J. Geophys. Res.-Atmos., 118, 8320–8332, https://doi.org/10.1002/jgrd.50646, 2013b.
Kravitz, B., MacMartin, D. G., Wang, H., and Rasch, P. J.: Geoengineering as a design problem, Earth Syst. Dynam., 7, 469–497, https://doi.org/10.5194/esd-7-469-2016, 2016.
Kravitz, B., MacMartin, D. G., Mills, M. J., Richter, J. H., Tilmes, S., Lamarque, J.-F., Tribbia, J. J., and Vitt, F.: First simulations of designing stratospheric sulfate aerosol geoengineering to meet multiple simultaneous climate objectives, J. Geophys. Res.-Atmos., 122, 12616–12634, https://doi.org/10.1002/2017JD026874, 2017.
Kuebbeler, M., Lohmann, U., and Feichter, J.: Effects of stratospheric sulfate aerosol geo-engineering on cirrus clouds, Geophys. Res. Lett., 39, L23803, https://doi.org/10.1029/2012GL053797, 2012.
Liepert, B. G. and Previdi, M.: Do models and observations disagree on the rainfall response to global warming?, J. Climate, 22, 3156–3166, https://doi.org/10.1175/2008JCLI2472.1, 2009.
MacMartin, D. G., Kravitz, B., Tilmes, S., Richter, J. H., Mills, M. J., Lamarque, J.-F., Tribbia, J. J., and Vitt, F.: The climate response to stratospheric aerosol geoengineering can be tailored using multiple injection locations, J. Geophys. Res.-Atmos., 122, 12574–12590, https://doi.org/10.1002/2017JD026868, 2017.
Marsh, D. R., Mills, M. J., Kinnison, D. E., Lamarque, J.-F., Calvo, N., and Polvani, L. M.: Climate Change from 1850 to 2005 Simulated in CESM1(WACCM), J. Climate, 26, 7372–7391, https://doi.org/10.1175/JCLI-D-12-00558.1, 2013.
Mercado, L. M., Bellouin, N., Sitch, S., Boucher, O., Huntingford, C., Wild, M., and Cox, P. M.: Impact of changes in diffuse radiation on the global land carbon sink, Nature, 458, 1014–1017, https://doi.org/10.1038/nature07949, 2009.
Modak, A. and Bala, G.: Sensitivity of simulated climate to latitudinal distribution of solar insolation reduction in solar radiation management, Atmos. Chem. Phys., 14, 7769–7779, https://doi.org/10.5194/acp-14-7769-2014, 2014.
Modak, A., Bala, G., Cao, L., and Caldeira, K.: Why must a solar forcing be larger than a CO2 forcing to cause the same global mean surface temperature change?, Environ. Res. Lett., 11, 044013, https://doi.org/10.1088/1748-9326/11/4/044013, 2016.
Modak, A., Bala, G., Caldeira, K., and Cao, L.: Does shortwave absorption by methane influence its effectiveness?, Clim. Dynam., 51, 3653–3672, https://doi.org/10.1007/s00382-018-4102-x, 2018.
Nalam, A., Bala, G., and Modak, A.: Effects of Arctic geoengineering on precipitation in the tropical monsoon regions, Clim. Dynam., 50, 3375–3395, https://doi.org/10.1007/s00382-017-3810-y, 2017.
Neale, R. B., Richter, J. H., Conley, A. J., Park, S., Lauritzen, P. H., Gettelman, A., Williamson, D. L., Rasch, P. J., Vavrus, S. J., Taylor, M. A., Collins, W. D., Zhang, M., and Lin, S.: Description of the NCAR Community Atmosphere Model (CAM 4.0), NCAR Tech. Note NCAR/TN-485+STR, National Center for Atmospheric Research, Boulder, Colorado, USA, 2010.
Niemeier, U. and Schmidt, H.: Changing transport processes in the stratosphere by radiative heating of sulfate aerosols, Atmos. Chem. Phys., 17, 14871–14886, https://doi.org/10.5194/acp-17-14871-2017, 2017.
Niemeier, U. and Timmreck, C.: What is the limit of climate engineering by stratospheric injection of SO2?, Atmos. Chem. Phys., 15, 9129–9141, https://doi.org/10.5194/acp-15-9129-2015, 2015.
Niemeier, U., Schmidt, H., and Timmreck, C.: The dependency of geoengineered sulfate aerosol on the emission strategy, Atmos. Sci. Lett., 12, 189–194, https://doi.org/10.1002/asl.304, 2011.
Niemeier, U., Schmidt, H., Alterskjær, K., and Kristjánsson, J. E.: Solar irradiance reduction via climate engineering: Impact of different techniques on the energy balance and the hydrological cycle, J. Geophys. Res.-Atmos., 118, 11905–11917, https://doi.org/10.1002/2013JD020445, 2013.
Oleson, K. W., Lawrence, D. M., Bonan, G. B., Flanner, M. G., Kluzek, E., Lawrence, P. J., Levis, S., Swenson, S. C., Thornton, P. E., Dai, A., Decker, M., Dickinson, R., Feddema, J., Heald, C. L., Hoffman, F., Lamarque, J.-F., Mahowald, N., Niu, G.- Y., Qian, T., Randerson, J., Running, S., Sakaguchi, K., Slater, A., Stöckli, R., Wang, A., Yang, Z.-L., Zeng, X., and Zeng, X.: Technical Description of version 4.0 of the Community Land Model (CLM), Tech. rep., National Center for Atmospheric Research, Boulder, Colorado, 2010.
Owensby, C. E., Ham, J. M., Knapp, A. K., and Auen, L. M.: Biomass production and species composition change in a tall grass prairie ecosystem after long-term exposure to elevated atmospheric CO2, Glob. Change Biol., 5, 497–506, https://doi.org/10.1046/j.1365-2486.1999.00245.x, 1999.
Pinker, R. T. and Laszlo, I.: Global distribution of photosynthetically active radiation as observed from satellites, J. Climate, 5, 56–65, https://doi.org/10.1175/1520-0442(1992)005<0056:GDOPAR>2.0.CO;2, 1992.
Pope, F. D., Braesicke, P., Grainger, R. G., Kalberer, M., Watson, I. M., Davidson, P. J., and Cox, R. A.: Stratospheric aerosol particles and solar-radiation management, Nat. Clim. Change, 2, 713–719, https://doi.org/10.1038/nclimate1528, 2012.
Rasch, P. J., Crutzen, P. J., and Coleman, D. B.: Exploring the geoengineering of climate using stratospheric sulfate aerosols: The role of particle size, Geophys. Res. Lett., 35, L02809, https://doi.org/10.1029/2007GL032179, 2008.
Richter, J. H., Tilmes, S., Mills, M. J., Tribbia, J. J., Kravitz, B., MacMartin, D. G., Vitt, F., and Lamarque, J.-F.: Stratospheric Dynamical Response and Ozone Feedbacks in the Presence of SO2 Injections, J. Geophys. Res.-Atmos., 122, 12557–12573, https://doi.org/10.1002/2017JD026912, 2017.
Robock, A.: Volcanic eruptions and climate, Rev. Geophys., 38, 191–219, https://doi.org/10.1029/1998RG000054, 2000.
Rustad, L. E., Campbell, J. L., Marion, G. M., Norby, R. J., Mitchell, M. J., Hartley, A. E., Cornelissen, J. H. C., Gurevitch, J., and GCTE NEWS: A meta-analysis of the response of soil respiration, net nitrogen mineralization, and aboveground plant growth to experimental ecosystem warming, Oecologia, 126, 543–562, https://doi.org/10.1007/s004420000544, 2001.
Schmidt, H., Alterskjær, K., Bou Karam, D., Boucher, O., Jones, A., Kristjánsson, J. E., Niemeier, U., Schulz, M., Aaheim, A., Benduhn, F., Lawrence, M., and Timmreck, C.: Solar irradiance reduction to counteract radiative forcing from a quadrupling of CO2: climate responses simulated by four earth system models, Earth Syst. Dynam., 3, 63–78, https://doi.org/10.5194/esd-3-63-2012, 2012.
Smith, K. L., Neely, R. R., Marsh, D. R., and Polvani, L. M.: The Specified Chemistry Whole Atmosphere Community Climate Model (SC-WACCM), J. Adv. Model. Earth Sy., 6, 883–901, https://doi.org/10.1002/2014MS000346, 2015.
Soden, B. J., Wetherald, R. T., Stenchikov, G. L., and Robock, A.: Global cooling after the eruption of Mount Pinatubo: a test of climate feedback by water vapor, Science, 296, 727–730, https://doi.org/10.1126/science.296.5568.727, 2002.
Stenchikov, G. L., Kirchner, I., Robock, A., Graf, H-F., Antuña, J. C., Grainger, R. G., Lambert, A., and Thomason, L.: Radiative forcing from the 1991 Mount Pinatubo volcanic eruption, J. Geophys. Res., 103, 13837–13857, https://doi.org/10.1029/98JD00693, 1998.
Storelvmo, T., Kristjansson, J. E., Muri, H., Pfeffer. M., Barahona, D., and Nenes, A.: Cirrus cloud seeding has potential to cool climate, Geophys. Res. Lett., 40, 178–182, https://doi.org/10.1029/2012GL054201, 2013.
Tilmes, S. and Mills, M.: Stratospheric Sulfate Aerosols and Planetary Albedo, in: Global Environmental Change, Handbook of Global Environmental Pollution, Vol., 1, edited by: Freedman, B., Springer, Dordrecht, 2014.
Tilmes, S., Fasullo, J., Lamarque, J.-F., Marsh, D. R., Mills, M., Alterskjær, K., Muri, H., Kristjánsson, J. E., Boucher, O., Schulz, M., Cole, J. N. S., Curry, C. L., Jones, A., Haywood, J., Irvine, P. J., Ji, D., Moore, J. C., Karam, D. B., Kravitz, B., Rasch, P. J., Singh, B., Yoon, J.-H., Niemeier, U., Schmidt, H., Robock, A., Yang, S., and Watanabe, S.: The hydrological impact of geoengineering in the Geoengineering Model Intercomparison Project (GeoMIP), J. Geophys. Res.-Atmos., 118, 11036–11058, https://doi.org/10.1002/jgrd.50868, 2013.
Tilmes, S., Lamarque, J.-F., Emmons, L. K., Kinnison, D. E., Ma, P.-L., Liu, X., Ghan, S., Bardeen, C., Arnold, S., Deeter, M., Vitt, F., Ryerson, T., Elkins, J. W., Moore, F., Spackman, J. R., and Val Martin, M.: Description and evaluation of tropospheric chemistry and aerosols in the Community Earth System Model (CESM1.2), Geosci. Model Dev., 8, 1395–1426, https://doi.org/10.5194/gmd-8-1395-2015, 2015.
Tilmes, S., Richter, J. H., Mills, M. J., Kravitz, B., MacMartin, D. G., Vitt, F., Tribbia, J. J., and Lamarque, J.-F.: Sensitivity of Aerosol Distribution and Climate Response to Stratospheric SO2 Injection Locations, J. Geophys. Res.-Atmos., 122, 12591–12615, https://doi.org/10.1002/2017JD026888, 2017.
Tilmes, S., Richter, J. H., Kravitz, B., MacMartin, D. G., Mills, M. J., Simpson, I. R., Glanville, A. S., Fasullo, J. T., Phillips, A. S., Lamarque, J.-F., Tribbia, J., Edwards, J., Mickelson, S., and Gosh, S.: CESM1(WACCM) Stratospheric Aerosol Geoengineering Large Ensemble (GLENS) Project, B. Am. Meteorol. Soc., 99, 2361–2371, https://doi.org/10.1175/BAMS-D-17-0267.1, 2018a.
Tilmes, S., Richter, J. H., Mills, M. J., Kravitz, B., MacMartin, D. G., Garcia, R. R., Kinnison, D. E., Lamarque, J.-F., Tribbia, J., and Vitt, F.: Effects of different Stratospheric SO2 Injection Altitudes on Stratospheric Chemistry and Dynamics, J. Geophys. Res.-Atmos., 123, 4654–4673, https://doi.org/10.1002/2017JD028146, 2018b.
Visioni, D., Pitari, G., di Genova, G., Tilmes, S., and Cionni, I.: Upper tropospheric ice sensitivity to sulfate geoengineering, Atmos. Chem. Phys., 18, 14867–14887, https://doi.org/10.5194/acp-18-14867-2018, 2018.
Weisenstein, D. K., Keith, D. W., and Dykema, J. A.: Solar geoengineering using solid aerosol in the stratosphere, Atmos. Chem. Phys., 15, 11835–11859, https://doi.org/10.5194/acp-15-11835-2015, 2015.
Xia, L., Robock, A., Tilmes, S., and Neely III, R. R.: Stratospheric sulfate geoengineering could enhance the terrestrial photosynthesis rate, Atmos. Chem. Phys., 16, 1479–1489, https://doi.org/10.5194/acp-16-1479-2016, 2016.