the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The response of precipitation characteristics to global warming from climate projections
Filippo Giorgi
Francesca Raffaele
Erika Coppola
We revisit the issue of the response of precipitation characteristics to global warming based on analyses of global and regional climate model projections for the 21st century. The prevailing response we identify can be summarized as follows: increase in the intensity of precipitation events and extremes, with the occurrence of events of “unprecedented” magnitude, i.e., a magnitude not found in the present-day climate; decrease in the number of light precipitation events and in wet spell lengths; and increase in the number of dry days and dry spell lengths. This response, which is mostly consistent across the models we analyzed, is tied to the difference between precipitation intensity responding to increases in local humidity conditions and circulations, especially for heavy and extreme events, and mean precipitation responding to slower increases in global evaporation. These changes in hydroclimatic characteristics have multiple and important impacts on the Earth's hydrologic cycle and on a variety of sectors. As examples we investigate effects on potential stress due to increases in dry and wet extremes, changes in precipitation interannual variability, and changes in the potential predictability of precipitation events. We also stress how the understanding of the hydroclimatic response to global warming can provide important insights into the fundamental behavior of precipitation processes, most noticeably tropical convection.
- Article
(8301 KB) -
Supplement
(3409 KB) - BibTeX
- EndNote
One of the greatest concerns regarding the effects of climate change on human societies and natural ecosystems is the response of the Earth's hydrologic cycle to global warming. In fact, by affecting the surface energy budget, warming induced by greenhouse gas (GHG), along with related feedback processes (e.g., water vapor, ice albedo and cloud feedbacks), can profoundly affect the Earth's water cycle (e.g., Trenberth et al., 2003; Held and Soden, 2006; Trenberth, 2011; IPCC, 2012).
The main engine for the Earth's hydrologic cycle is the radiation from the Sun, which heats the surface and causes evaporation from the oceans and land. Total surface evaporation has been estimated at 486×103 km3 year−1 of water, of which 413×103 km3 year−1, or ∼85 %, is from the oceans and the rest from land areas (Trenberth et al., 2007). Once in the atmosphere, water vapor is transported by the winds until it eventually condenses and forms clouds and precipitation. The typical atmospheric lifetime of water vapor is several days, and therefore at climate timescales there is essentially an equilibrium between global surface evaporation and precipitation. Total mean precipitation as been estimated at 373×103 km3 year−1 of water over oceans and 113×103 km3 year−1 over land (adding up to the same global value as evaporation; Trenberth et al., 2007). Water precipitating over land can then either reevaporate or flow into the oceans through surface runoff or subsurface flow.
Given this picture of the hydrologic cycle, however, it is important to stress that, although evaporation and precipitation globally balance out, their underlying processes are very different. Evaporation is a continuous and slow process (globally about ∼2.8 mm day−1, Trenberth et al., 2007), while precipitation is a highly intermittent, fast and localized phenomenon, with precipitation events drawing moisture only from an area about 3–5 times the size of the event itself (Trenberth et al., 2003). In addition, on average, only about 25 % of days are rainy days, but since it does not rain throughout the entire day, the actual fraction of time it rains has been estimated at 5 %–10 % (Trenberth et al., 2003). In other words, most of the time it does not actually rain.
This has important implications for the assessment of hydroclimatic responses to global warming because it may not be very meaningful, and certainly not sufficient, to analyze mean precipitation fields, but it is necessary to also investigate higher-order statistics. For example, the same mean of 1 mm day−1 could derive from 10 consecutive 1 mm day−1 events, a single 10 mm day−1 event with 9 dry days or two 5 mm day−1 events separated by a dry period. Each of these cases would have a very different impact on societal sectors or ecosystem dynamics.
This consideration also implies that the impact of global warming on the Earth's hydroclimate might actually manifest itself not only as a change in mean precipitation but also, perhaps more markedly, as variations in the characteristics and regimes of precipitation events. This notion has been increasingly recognized since the pioneering works of Trenberth (1999) and Trenberth et al. (2003), with many studies looking particularly at changes in the frequency and intensity of extreme precipitation events (e.g., Easterling et al., 2000; Christensen and Christensen, 2003; Tebaldi et al., 2006; Allan and Soden, 2008; Giorgi et al., 2011, 2014a, b; IPCC, 2012; Sillmann et al., 2013b; Pendergrass and Hartmann, 2014; Sedlacek and Knutti, 2014; Pfahl et al., 2017; Thackeray et al., 2018).
In this paper, which presents a synthesis of the Alexander von Humboldt medal lecture given by the first author (FG) at the European Geosciences Union (EGU) General Assembly in 2018, we revisit some of the concepts related to the issue of the impacts of global warming on the characteristics of the Earth's hydroclimate, stressing that it is not our purpose to provide a review of the extensive literature on this topic. Rather, we want to illustrate some of the points made above through relevant examples obtained from new and past analyses of global and regional climate model projections carried out by the authors.
More specifically, we will draw from global climate model (GCM) projections carried out as part of the CMIP5 program (Taylor et al., 2012) and regional climate model (RCM) projections from the COordinated Regional climate Downscaling EXperiment (CORDEX; Giorgi et al., 2009; Jones et al., 2011; Gutowski Jr. et al., 2016), which downscale CMIP5 GCM data. In this regard, we focus on the high-end RCP8.5 scenario (Moss et al., 2010), in which the ensemble mean global temperature increase by 2100 is about 4 ∘C (±1 ∘C) compared to late 20th century temperatures (IPCC, 2013), stressing that results for lower GHG scenarios are qualitatively similar to those found here but of smaller magnitude (not shown for brevity).
In the next sections we first summarize the changes in mean precipitation fields in our ensemble of model projections and then explore the response of different precipitation characteristics, trying specifically to identify robust responses. After having identified the dominant hydroclimatic responses, we discuss examples of their impact on different quantities of relevance for socioeconomic impacts, specifically the potential stress associated with changes in dry and wet extreme events, precipitation interannual variability, and the predictability of precipitation events.
Throughout this paper we mostly base our analysis on the 10 CMIP5 GCMs used by Giorgi et al. (2014a) for easier comparison with, and reference to, this previous work. These 10 models were chosen because they were the only ones among the full CMIP5 dataset for which daily data were available at the time the analysis of Giorgi et al. (2014a) was carried out. This sub-ensemble includes some of the most commonly used models, and an analysis of mean and seasonal data by Giorgi et al. (2014a) showed that it behaves quite similarly to the full CMIP5 ensemble. In addition, as will be seen later, a high level of consistency is found in the behavior of these models also concerning daily statistics, and therefore we feel that this 10-GCM ensemble is at least qualitatively representative of the full CMIP5 set.
2.1 Mean precipitation changes
In general, as a result of the warming of the oceans and land, global surface evaporation increases with increasing GHG forcing. This increase mostly lies in the range of 1 %–2 % per degree of surface global warming (% per DGW; Trenberth et al., 2007). As a consequence, global mean precipitation also tends to increase roughly by the same amount. This has been found in most GCM projections, as illustrated in the examples in Fig. 1.
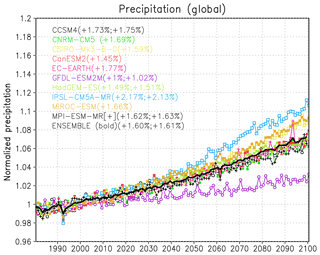
Figure 1Normalized mean global precipitation from 1981 to 2100 in the 10 CMIP5 GCM simulations for the RCP8.5 scenario used by Giorgi et al. (2014a), along with their ensemble average. The first number in parentheses shows the corresponding mean global precipitation change per degree of global warming, while the second shows (for a subset of models with available data) the same quantity for global surface evaporation. The annual precipitation is normalized by the mean precipitation during the reference period 1981–2010; therefore, a value of, e.g., 1.1 indicates an increase of 10 %.
Although precipitation increases globally, at the regional level we can find relatively complex patterns of change, with areas of increased and areas of decreased precipitation. These patterns are closely related to changes in global circulation features, global energy and momentum budgets, local forcings (e.g., topography, land use), and energy and water fluxes affecting convective activity (e.g., Thackeray et al., 2018). The basic geographical structure of precipitation change patterns has been quite resilient throughout different generations of GCM projections, at least in an ensemble-averaged sense. These precipitation change patterns are shown in Fig. 2 as obtained from the CMIP5 ensemble, but they are similar in the CMIP3 and earlier GCM ensembles.
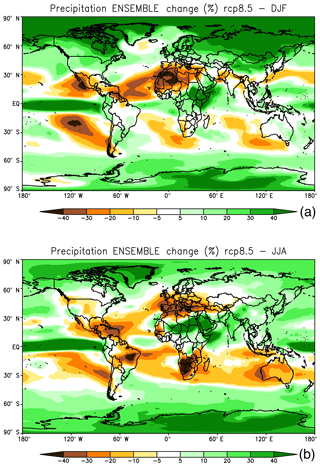
Figure 2Ensemble mean change in precipitation (RCP8.5, 2071–2100 minus 1981–2010) for December–January–February (a) and June–July–August (b) in the CMIP5 ensemble of models.
The increase in precipitation at middle to high latitudes has been attributed to a poleward shift of the storm tracks associated with maximum warming in the tropical troposphere (due to enhanced convection), which in turn produces a poleward shift of the maximum horizontal temperature gradient and jet stream location (e.g., IPCC, 2013). This process is essentially equivalent to a poleward expansion of the Hadley cell, which also causes drier conditions in subtropical areas, including the Mediterranean and Central America–Southwestern US regions. The Intertropical Convergence Zone (ITCZ) shows narrowing and greater precipitation intensity, especially in the core of the Pacific ITCZ, associated with increased organized deep convective activity towards the ITCZ center and decreased activity along its edges (Byrne et al., 2018). Finally, over monsoon regions, a general increase in precipitation has been attributed to a greater water-holding capacity of the atmosphere counterbalancing a decrease in monsoon circulation strength (IPCC, 2013); however, more detailed analyses of how global constraints on energy and momentum budgets affect regional-scale circulations are needed for a better understanding of the monsoon response to global warming (Biasutti et al., 2018).
As already mentioned, these broad-scale change patterns have been confirmed by different generations of GCM projections and thus appear to be robust model-derived signals. On the other hand, high-resolution RCM experiments have shown that local forcings associated with complex topography and coastlines can substantially modulate these large-scale signals, often to the point of being of opposite sign. For example, the precipitation shadowing effect of major mountain systems tends to concentrate precipitation increases towards the upwind side of the mountains and to reduce the increases or even generate decreases in precipitation in the lee side (e.g., Giorgi et al., 1994; Gao et al., 2006). Similarly, in the summer, the precipitation change signal can be strongly affected by high-elevation warming and wetting, which enhance local convective activity. For example, Giorgi et al. (2016) found enhanced precipitation over the Alpine high peaks in high-resolution EURO-CORDEX (Jacob et al., 2014) and MED-CORDEX (Ruti et al., 2016) projections, whereas the driving coarse-resolution global models produced a decrease in precipitation. In addition to these local effects, it has been found that the simulation of some modes of variability, such as blocking events, is also sensitive to model resolution (e.g., Anstey et al., 2013; Schiemann et al., 2017). As a result of all these processes it is thus possible that the large-scale precipitation change patterns in Fig. 2 might be significantly modified as we move to substantially higher-resolution models.
On the other hand, a key question concerning the precipitation response to global warming is the following: How will precipitation change patterns affect different socioeconomic sectors? This question depends more on the modifications of the characteristics of precipitation than the mean precipitation itself. For example, changes in precipitation interannual variability may have strong impacts on crop planning. As another example, if an increase in precipitation is due to an increase in extreme damaging events, this will have negative rather than positive impacts. Alternatively, if the increase is due to very light events that do not replenish the soil of moisture, this will not constitute an added water resource. Conversely, a reduction of precipitation mostly associated with a reduction of extremes will result in positive rather than negative impacts. It is thus critical to assess how the characteristics of precipitation will respond to global warming, which is the focus of the next sections.
2.2 Daily precipitation intensity probability density functions (PDFs)
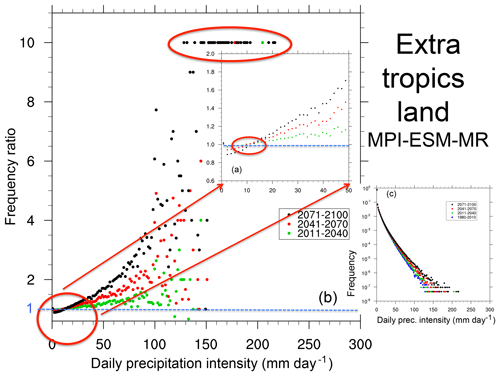
Daily precipitation is one of the variables most often used in impact assessment studies, and therefore an effective way to investigate the response of precipitation characteristics to global warming is to assess changes in daily precipitation intensity PDFs. As an illustrative example of PDF changes, Figs. 3 and 4 show normalized precipitation intensity PDFs for four time slices: 1981–2010 (reference period representative of present-day conditions), 2011–2040, 2041–2070 and 2071–2100 in the MPI-ESM-MR RCP8.5 projection of the CMIP5 ensemble. The further the time slice is in the future, the greater the warming (up to a maximum of about 4 ∘C in 2071–2100). The variable shown, which we refer to as PDF, is the frequency of occurrence of precipitation events within a certain interval (bin) of intensity normalized by the total number of days, including non-precipitating days.
Note that in the MPI-ESM-MR model the response of mean global precipitation to global warming is in line with the model ensemble average (Fig. 1), while the response of daily statistics is among the strongest (see, e.g., Giorgi et al., 2014a and Table 1), but qualitatively consistent with most other models (see below). Therefore, this model is illustrative of the simulated precipitation response to global warming in the subset of CMIP5 GCMs analyzed.
Table 1Change in different daily precipitation indicators between 2071–2100 and 1976–2005 for the 10 CMIP5 GCMs of Giorgi et al. (2014a) expressed in % per degree of surface global warming over global (upper box) and global land (lower box) areas; “global” means the area between 60∘ S and 60∘ N. SDII is the precipitation intensity, 95p, 99p and 99.9p are the 95th, 99th and 99.9th percentiles, respectively, and the precipitation change only include wet days, i.e., days with precipitation greater than 1 mm day−1.

Also, as in our previous work (Giorgi et al., 2014a), throughout this paper a rainy day is considered as having a precipitation amount of at least 1 mm day−1 so that drizzle days are removed. In this regard, the choice of a precipitation threshold to define a rainy day makes the calculation of precipitation frequency and intensity dependent on the resolution of the data (e.g., Chen and Dai, 2018). Attention should be paid to this issue when analyzing precipitation statistics and here, as well as in previous work, we conduct direct cross-model or data–model intercomparisons only after having interpolated the data onto common grids.
Finally, given the logarithmic scale of the frequency of occurrence, in order to better illustrate changes in frequencies, Figs. 3 and 4 report the ratio of the frequency of occurrence for a given bin in a future time slice divided by the same quantity in the reference period. Averaged data are shown for land areas in the tropics (30∘ S–30∘ N; Fig. 3) and extratropical midlatitudes (30–60∘ N and S; Fig. 4), noting that qualitatively similar results were found for ocean areas.
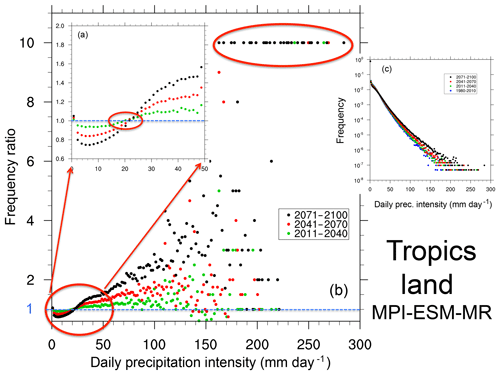
Figure 3(a) A zoomed-in view of the part of the curves highlighted by the corresponding red oval. Ratio values of 10 (highlighted with a red oval) are used when events occur in the future time slice that are not present in the reference period for a given intensity bin. (b) Ratio of future to reference normalized frequency of daily precipitation intensity for the three future time slices. (c) Probability density function (PDF) defined as the normalized frequency of occurrence of daily precipitation events of intensity within a certain bin interval over land regions in the tropics (30∘ S–30∘ N) for the reference period 1981–2010 and three future time slices (2011–2040, 2041–2070, 2071–2100) in the MPI-ESM-MR model. The frequency is normalized by the total number of days (including dry days, i.e., days with precipitation lower than 1 mm day−1).
The PDFs exhibit a log-linear relationship between intensities and frequencies, with a sharp drop in frequency as the intensity increases. The ratios of future vs. present-day frequencies consistently show the following features.
-
An increase in the number of dry days, as seen from the ratios >1 in the first bin (precipitation less than 1 mm day−1), i.e., a decrease in the frequency of wet events. Note that, even if these ratios are only slightly greater than 1, because the frequencies of dry days are much higher than those of wet days, the actual absolute increase in the number of dry days is relatively high.
-
A decrease (ratio <1) in the frequency of light to medium precipitation events up to a certain intensity threshold. In the models we analyzed, when taken over large areas, this threshold lies around the 95th percentile of the full distribution and is higher for tropical than extratropical land regions because of the higher amounts of precipitation in tropical convection systems. Interestingly, while the threshold depends on latitude, it is approximately invariant for all future time slices, i.e., it appears to be relatively independent of the level of warming. The decrease in light precipitation events has been at least partially attributed to an increase in thermal stability induced by the GHG forcing (Chou et al., 2012).
-
An increase (ratio >1) in the frequency of events for intensities higher than the threshold mentioned above. The relative increase in frequency grows with the intensity of the events, and it is thus maximum for the highest-intensity events, an indication of a nonlinear response of the precipitation intensity to warmer conditions. Note that, because of the logarithmic frequency scale, the absolute increase in the number of high-intensity events is relatively low.
-
The occurrence in future time slices of events with intensity well beyond the maximum found in the reference period. These are illustrated by the prescribed value of 10 when events occurred for a given bin in the future time slice, but not in the reference one. One could thus interpret these as occurrences of “unprecedented” events.
-
All the features 1–4 tend to amplify as the time slice is further into the future, i.e., as the level of warming increases, and are generally more pronounced over tropical than extratropical areas (and over land than ocean regions, which we did not show for brevity).
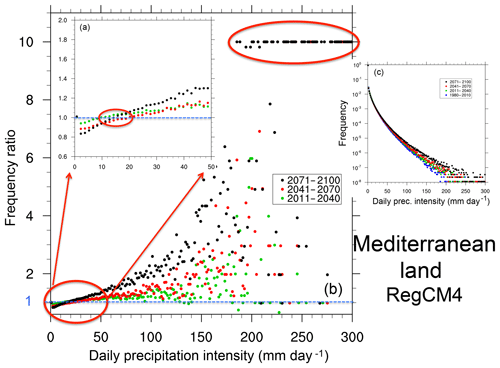
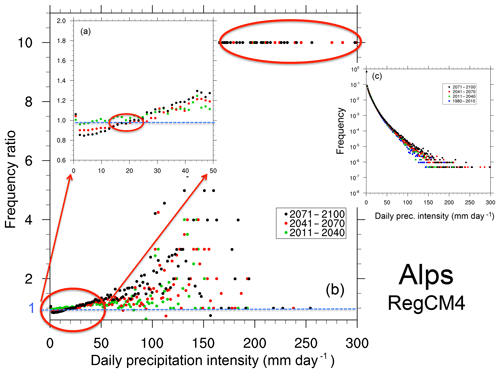
Although the results in Figs. 3 and 4 are obtained from one model, they are qualitatively consistent with those we found for other CMIP5 GCMs. As an example, results analogous to those in Figs. 3 and 4, but for the HadGEM and EC-Earth GCMs, are reported in Supplement Figs. S1 and S2. We also carried out the same type of analysis for a high-resolution RCM projection (12 km grid spacing, RCP8.5 scenario) conducted with the RegCM4 model (Giorgi et al., 2012) over the Mediterranean domain defined for the MED-CORDEX program (Ruti et al., 2016). Figures 5 and 6 show PDFs and PDF ratios for three 30-year future time slices calculated over land areas throughout the Mediterranean domain and over a subarea covering the Alpine region. They show features similar to those found for the GCMs, with the signal over the Alpine region being more pronounced than for the entire Mediterranean area. As further examples, Supplement Figs. S3 and S4 report similar plots computed over the entire European land territory for EURO-CORDEX simulations with the REMO and RACMO RCMs, which show features qualitatively in line with those of Figs. 5 and 6. In addition, our results are also consistent with previous analyses of RCM projections (e.g., Gutowski Jr. et al., 2007; Boberg et al., 2009; Jacob et al., 2014; Giorgi et al., 2014b), suggesting that the projected changes in the precipitation intensity PDFs summarized in points 1–4 above are generally robust across a wide range of models and model resolutions.
2.3 Hydroclimatic indices
The changes in precipitation intensity PDFs found in the previous section should be reflected in, and measured by, changes in hydroclimatic indices representative of given precipitation regimes. In two previous studies (Giorgi et al., 2011, 2014a), we assessed the changes in a series of interconnected hydroclimatic indices in an ensemble of 10 CMIP5 projections. The indices analyzed include the following.
-
SDII: mean precipitation intensity (including only wet events)
-
DSL: mean dry spell length, i.e., mean length of consecutive dry days
-
WSL: mean wet spell length, i.e., mean length of consecutive wet days
-
R95: fraction of total precipitation above the 95th percentile of the daily precipitation intensity distribution during the reference period 1981–2010
-
PA: precipitation area, i.e., the total area covered by wet events on any given day
-
HY-INT, i.e., the hydroclimatic intensity index introduced by Giorgi et al. (2011) consisting of the product of normalized SDII and DSL
Note that the PA and HY-INT indices were specifically introduced by Giorgi et al. (2011, 2014a). The PA is the spatial counterpart of the mean frequency of precipitation days, while the HY-INT was introduced under the assumption that the changes in SDII and DSL are interconnected responses to global warming (Giorgi et al., 2011).
Giorgi et al. (2011, 2014a) examined changes in these indices for ensembles of CMIP3 and CMIP5 GCM projections, as well as a number of RCM projections, in future time slices with respect to the 1976–2005 reference period. Their results, which were consistently found for most models analyzed, indicated a prevalent increase in SDII, R95, HY-INT and DSL and a decrease in PA and WSL. Similar results were then found by Giorgi et al. (2014b) in an analysis of multiple RegCM4-based projections over five CORDEX domains. In other words, under warmer climate conditions, precipitation events are expected to be more intense and extreme and are temporally more concentrated and less frequent, which implies a reduction of the areas occupied by rain at any given time (although not necessarily a reduction of the size of the events). This response, which is consistent with the change in PDFs illustrated in Figs. 3–6, will hereafter be referred to as the higher intensity-reduced frequency (HIRF) precipitation response.
Giorgi et al. (2011, 2014a) also analyzed a global and several regional daily precipitation gridded observation datasets and found that trends for the period 1976–2005 were predominantly in line with the model-projected changes over most continental areas. Further evidence of increases in heavy precipitation events in observational records is, for example, reported by Fischer and Knutti (2016) and references therein; however, this conclusion cannot be considered entirely robust and needs to be verified with further analysis due to the high uncertainty in precipitation observations (e.g., Herold et al., 2017).
An explanation for the HIRF hydroclimatic response to global warming is related to the fact that, on the one hand, the mean global precipitation change roughly follows the mean global evaporation increase, i.e., 1.5–2.0 % per DGW (Trenberth et al., 2007, Fig. 1). On the other hand, the intensity of precipitation, in particular for high and extreme precipitation events, is more tied to the increase in the water-holding capacity of the atmosphere, which is in turn regulated by the Clausius–Clapeyron (Cl–Cl) response of about 7 % per DGW, although the precipitation response is modulated by regional and local circulations along with energy and water fluxes, which might lead to super-Cl–Cl or sub-Cl–Cl responses (e.g., Trenberth et al., 2003; Pall et al., 2007; Lenderink and van Meijgaard, 2008; Chou et al., 2012; Singleton and Toumi, 2013; Pendergrass and Hartmann, 2014; Ivancic and Shaw, 2016; Fischer and Knutti, 2016; Pfahl et al., 2017). Therefore, the increase in precipitation intensity can be expected to be generally larger than the increase in mean precipitation, which implies a decrease in precipitation frequency.
To illustrate this point, Table 1 reports the globally averaged changes (2071–2100 minus the reference period 1976–2005, as in Giorgi et al., 2014a; RCP8.5 scenario) in mean precipitation, precipitation intensity and frequency, and the 95th, 99th and 99.9th percentiles of daily precipitation for the 10 GCMs of Giorgi et al. (2014a), along with their ensemble average. The values of Table 1 were calculated as follows: we first computed the change in % per DGW at each model grid point and then averaged these values over global land + ocean as well as global land-only areas. This was done in order to avoid the possibility that areas with large precipitation amounts may dominate the average. On the other hand, grid-point normalization artificially amplifies the contribution of regions with small precipitation amounts, such as polar and desert areas. For this reason, as in Giorgi et al. (2014a), we did not include in the averaging areas north of 60∘ N and south of 60∘ S (polar regions) along with areas with mean annual precipitation lower than 0.5 mm day−1 (which effectively identifies desert regions). In addition, we did not consider precipitation associated with days with amounts of less than 1 mm day−1 in order to be consistent with our definition of a rainy day (which disregards drizzle events).
Also in these calculations, the increase in global mean precipitation is in the range of 1% per DGW to 2 % per DGW except for the GFDL experiment, which shows a very small increase (indicating that in this model most of the precipitation increase occurs in the polar regions). In all cases except for MIROC the increase in global SDII is greater than the increase in mean precipitation, resulting in a decrease in the number of rainy days. The changes in the 95th, 99th and 99.9th percentiles are maximum for the most extreme percentiles, showing that the main contribution to the HIRF response is due to the highest-intensity events, i.e., above the 99th and 99.9th percentiles, whose response becomes increasingly closer to the Cl–Cl one (and even super-Cl–Cl for the GFDL model). In fact, the increase in the 95th percentile for the ensemble model average is lower than the increase in SDII, and this is because in some models the threshold intensity in Figs. 3–6, for which the sign of the change turns from negative to positive, lies beyond the 95th percentile. When only land areas between 60∘ S and 60∘ N are taken into account (bottom panel in Table 1), the changes are generally in line with the global ones, except for the CNRM model. Over land areas we also find changes in the highest percentiles of magnitude mostly greater than over the globe (and thus over oceans).
We can thus conclude that the shift to a regime of more intense but less frequent events in warmer conditions is due to the fact that precipitation intensity, especially for intense events (beyond the 95th percentile), responds at the local level primarily to the Cl–Cl-driven increase in water vapor amounts modulated by local circulations and fluxes, while mean precipitation responds to a slower evaporation process, driving a decrease in precipitation frequency. Noticeably, the MIROC experiment does not appear to follow this response; i.e., in this model the increase in mean precipitation appears to be driven by an increase in the number of light precipitation events.
While the data in Table 1 provide a diagnostic explanation for the HIRF response, it has also been suggested by very-high-resolution convection-permitting simulations that ocean temperatures might affect the self-organization and aggregation of convective systems (e.g., Mueller and Held, 2012; Becker et al., 2017), which would also affect the precipitation response to warming. Therefore, the study of the HIRF response might lead to a greater understanding of the fundamental behavior of the precipitation phenomenon, in particular tropical convection processes.
What are the consequences of the HIRF response to global warming? Obviously there can be many of them, but here we want to provide a few illustrative examples of relevance for impact applications.
3.1 Potential stress associated with wet and dry extreme events
The HIRF response suggests that global warming might induce an increase in the risk of damaging extreme wet and dry events, the former being associated with the increase in precipitation intensity and latter with the occurrence of longer sequences of dry days over areas of increasing size. In order to quantify this risk, in a recent paper (Giorgi et al., 2018; hereafter referred to as GCR18) we introduced a new index called the Cumulative Hydroclimatic Stress Index, or CHS. In GCR18, the CHS was calculated for two types of extreme events, the 99.9th percentile of the daily precipitation distribution (or R99.9) and the occurrence of at least three consecutive months experiencing a precipitation deficit with a magnitude greater than 25 % of the precipitation climatology for that month (or D25). Both of these metrics thus refer to extremely wet and dry events that can be expected to produce significant damage (see GCR18).
Taking as an example the R99.9, the CHS essentially cumulates the excess precipitation above the 99.9th percentile threshold calculated for a given reference period (e.g., 1981–2010). Hence, the assumption is that the potential stress associated with these extremes is proportional to the excess precipitation above the 99.9th percentile of the distribution. GCR18 calculated this quantity for a future climate projection and then normalized it by the corresponding value cumulated over the reference period. This normalization expresses the potential stress due to the increase in wet extremes in equivalent reference stress years (ERSYs), whereby an ERSY is the mean stress per year due to the extremes during the reference period (in our case 1981–2010). If, for example, a damage value can be assigned to such events, the ERSY can be interpreted as the mean yearly damage caused by extremes in present climate conditions. GCR18 then carried out similar calculations for the cumulative potential stress due to dry events by cumulating the deficit rain defined by the D25 metric. In addition, similarly to Diffenbaugh et al. (2007) and Sedlacek and Knutti (2014), they included exposure information within the definition of the CHS index by multiplying the excess or deficit precipitation by future population amounts (as obtained from Shared Socioeconomic Pathways, or SSPs; Rihai et al., 2016) normalized by present-day population values. The details of these calculations can be found in GCR18.
The main results of GCR18 are summarized in Figs. 7 and 8, which present maps of the potential cumulative stress due to both dry and wet events added by climate change during the period 2010–2100 and expressed in added ERSYs (i.e., after removing the value of 90 that would be obtained if no climate change occurred). The figures show the total ensemble-averaged added cumulative stress for the RCP8.5 scenario without (Fig. 7) and with (Fig. 8) the inclusion of population weighting (for which the SSP5 population scenario from Rihai et al., 2016, was used). The values in the figures were computed by first calculating the stress contribution in ERSYs of wet and dry extremes separately and then adding them so that there is no cancellation of stress if, for example, a wet extreme is followed by a dry extreme.
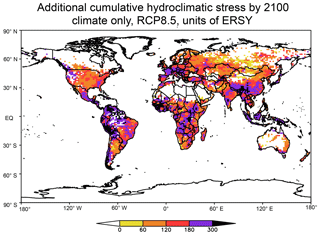
Figure 7Total number of additional stress years due to increases in wet (R99.9) and dry (D25) events for the period 2011–2100 including only climate variables for the RCP8.5 scenario (see text for more detail). Units are equivalent reference stress years (ERSYs) and the value does not include ERSYs obtained if climate did not change (i.e., for the period 2100–2011 a value of 90).
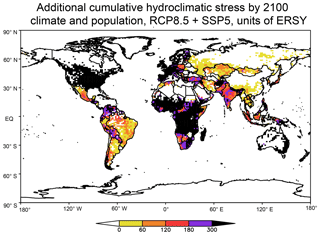
Figure 8Same as Fig. 7, but with the inclusion of the SSP5 population scenario (see text for more detail).
Figure 7 shows that, when only climate is accounted for, dry and wet extremes add more than 180 ERSYs (and in some cases more than 300 ERSYs) over extended areas of Central and South America, Europe, western and south–central Africa, and southern and southeastern Asia. In other words, the combined potential stress due to dry and wet extremes more than triples due to climate change by the end of the century. In this regard, GCR18 found that, when globally averaged over land regions and over all the models considered, both wet and dry extremes increased in the RCP8.5 scenario, the former adding ∼120 ERSYs and the latter adding ∼30 ERSYs.
When population scenarios are also accounted for (Fig. 8) the patterns of added cumulative stress are considerably modified. In this case, the total number of added ERSYs exceeds 300 over the entire continental US and Canada, most of Africa, Australia, and areas of South and Southeast Asia, which are projected to experience substantial population increases in the SSP5 scenario. Conversely, we find a reduced increase in stress over East and Southeast Asia, where the population is actually projected to decrease by the end of the 21st century (see GCR18). This result thus points to the importance of incorporating socioeconomic information in the assessment of the stress associated with climate-change-driven extreme events.
Notwithstanding the limitations and approximations of the approach of GCR18 amply discussed in that paper, the results in Figs. 7 and 8 clearly indicate that the increase in wet and dry extremes associated with global warming can constitute a serious threat to the socioeconomic development of various regions across all continents. GCR18 also show that the cumulative stress due to increases in extremes is drastically reduced under the RCP2.6 scenario, pointing to the importance of mitigation measures to reduce the level of global warming.
3.2 Impact on interannual variability
The interannual variability of precipitation is a key factor affecting many aspects of agriculture and water resources, and it is strongly affected by global modes of variability, such as the El Niño–Southern Oscillation (ENSO) in the tropics and the North Atlantic Oscillation (NAO) in midlatitudes. In this regard, the latest generation of GCM projections does not provide definitive indications concerning changes in the frequency or intensity of such modes (e.g., IPCC, 2013), although some works suggest the presence of robust changes in projected spatial patterns of ENSO-driven precipitation and temperature variability (e.g., Power et al., 2013).
Daily and seasonal precipitation statistics are not necessarily tied, since the same seasonal mean can be obtained via different sequences of daily precipitation events. In addition, the intensity distribution of daily and seasonal precipitation amounts can be quite different, the latter often being close to normal distributions (e.g., Giorgi and Coppola, 2009). On the other hand, the occurrence of longer dry spells, intensified by higher temperatures and lower soil moisture amounts, might be expected to amplify dry seasons, while the increase in the intensity of sequences of wet events might lead to amplified wet seasons. As a result, it can be expected that the HIRF regime response might lead to an increase in precipitation interannual variability.
To verify this hypothesis, we calculated for the GCM ensemble of Giorgi et al. (2014a) the change in precipitation interannual variability between future and present-day 30-year time slices using as a metric the coefficient of variation (CV). The CV is defined as the (in our case interannual) standard deviation normalized by the mean and has often been used as a measure of precipitation variability because it removes the strong dependence of precipitation variability on the mean itself (Raisanen, 2002; Giorgi and Bi, 2005).
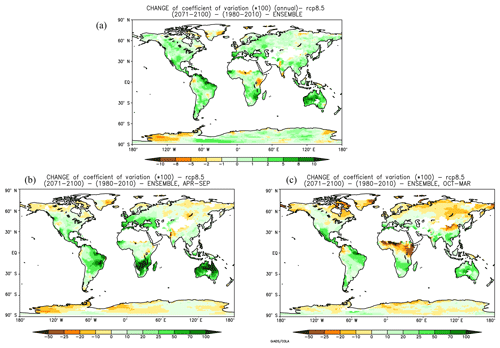
Figure 9Change in precipitation interannual coefficient of variation (2071–2100 vs. 1981–2010) for (a) mean annual precipitation, (b) April–September precipitation and (c) October–March precipitation.
Figure 9 shows the ensemble average change in precipitation CV between the 2071–2100 and 1981–2010 time slices for mean annual precipitation as well as precipitation averaged over the two 6-month periods April–September and October–March. It can be seen that, when considering annual averages, the interannual variability increases over the majority of land areas, with exceptions over small regions scattered throughout the different continents. When considering the two different 6-month seasons, in April–September (Northern Hemisphere summer, Southern Hemisphere winter) variability increases largely dominate, except over areas of the Northern Hemisphere high latitudes and some areas around major mountain systems. In October–March, the areas of decreased variability are more extended over northern Eurasia, northern North America and, interestingly, some equatorial African regions, although the increases are still somewhat more widespread.
Although Fig. 9 does not show a signal of ubiquitous sign across all land areas, it clearly points to a prevalent increase in interannual variability associated with global warming, at least as measured by the CV. It is important to note that this increase occurs in areas of both increased and decreased mean precipitation (see Fig. 2), so it is not strongly related to the use of the CV as a metric. Finally, this result is broadly consistent with analyses of previous-generation model projections (Raisanen, 2002; Giorgi and Bi, 2005; Pendergrass et al., 2017), which adds robustness to this conclusion.
3.3 Impact on precipitation predictability
A third issue we want to address concerns the possible effects of regime shifts on the predictability of precipitation, an issue that has obvious implications for a number of socioeconomic activities (e.g., agriculture, hazards, tourism, etc.). Indeed, precipitation is one of the most difficult meteorological variables to forecast, since it depends on both large-scale and complex local-scale processes (e.g., topographic forcing). While the chaotic nature of the atmosphere provides a theoretical limit to weather prediction of ∼10–15 days (e.g., Warner, 2010), the predictability range of different types of precipitation events depends crucially on the temporal scale of the dynamics related to the event itself. For example, the predictability range of synoptic systems is of the order of days, while that of long-lasting weather regimes, such as blockings, can be of weeks. It is thus clear that changes in precipitation regimes and statistics can lead to changes in the potential predictability of precipitation.
One of the benchmark metrics that is most often used to assess the skill of a prediction system is persistence (Warner, 2010). Essentially, persistence for a lead time T assumes that a given weather condition at a time t+T is the same as that at time t. In other words, when applied, for example, to daily precipitation, it assumes that, for a lead time of N days, if day i is wet (dry), day i+N will also be wet (dry). The skill of a forecast system is then measured by how much the forecast improves upon persistence. Therefore, persistence can be considered as a “minimum potential predictability”.
In order to assess whether global warming affects what we defined as the minimum potential predictability for precipitation, we calculated the percentage of successful precipitation forecasts obtained from persistence at lead times of 1, 3 and 7 days for the 10 GCM projections (RCP8.5) used by Giorgi et al. (2014a). This percentage, calculated year by year and then averaged over all land areas, is presented in Fig. 10, noting that the persistence forecast only concerns the occurrence of precipitation and not the amount.
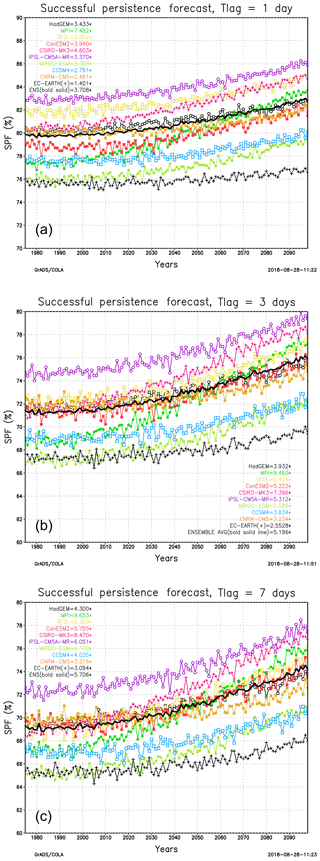
Figure 10Fraction of successful forecasts as a function of time using persistence for daily precipitation occurrence at time lags of (a) 1 day, (b) 3 days and (c) 7 days for the GCM ensemble of Giorgi et al. (2014a) (bold black line). The number in parenthesis denotes the trend in % per 100 years. Units are percentage of days in 1 year for which persistence provides a successful forecast (either dry or wet).
Figure 10 shows that in all model projections, and thus in the ensemble averages, the percent of successful persistence forecasts increases with global warming for all three time lags. This can be mostly attributed to the increase in mean dry spell length found in Sect. 2. For a lag time of 1 day, the successful persistence forecast in the model ensemble increases globally from about 80 % in 2010 to about 83 % in 2100, i.e., with a linear trend of ∼3.5 % per 100 years. As can be expected, the percentage of successful persistence forecasts decreases with the length of lag time: ∼76 % and 69 % in 2010 for lag times of 3 and 7 days, respectively. However, the growth rate of this percentage also increases with lag time: 5.2 % per 100 years and 5.7 % per 100 years for lag times of 3 and 7 days, respectively.
Despite the simplicity of the reasoning presented in this section, our results indicate that global warming can indeed affect (and in our specific case, increase) the potential predictability of the occurrence of dry vs. wet days. For example, persistence for the 7-day lag time has the same successful forecast rate by the middle of the 21st century as the present-day persistence for the 3-day lag time (∼71 %). Clearly, the issue of the effects of climate change on weather predictability is a very complex one, with many possible implications not only from the application point of view, but also for the assessment of the performance of forecast systems. It is thus important that this issue is addressed with more advanced techniques and metrics than we employed in our illustrative example.
In this paper we have revisited the basic responses of the characteristics of the Earth's hydroclimatology to global warming through the analysis of global and regional climate model projections for the 21st century. The projections examined suggested some robust hydroclimatic responses, in the sense of being mostly consistent across different model projections and being predominant over the majority of land areas. They can be summarized as follows:
-
a decrease (increase) in the frequency of wet (dry) days;
-
an increase in the mean length of dry spells;
-
an increase in the mean intensity of precipitation events;
-
an increase in the intensity and frequency of wet extremes;
-
a decrease in the frequency of light to medium precipitation events;
-
a decrease in the mean length of wet events and in the mean area covered by precipitation; and
-
the occurrence of wet events with a magnitude beyond that found in present climate conditions.
We discussed how this response is mostly tied to the different natures of the precipitation and evaporation processes, and we also presented some illustrative examples of the possible consequences of these responses, including an increase in the risks associated with wet and dry extremes, a predominant increase in the interannual variability of precipitation, and a modification of the potential predictability of precipitation events. In addition, some of results 1–7 above are consistent with previous analyses of global and regional model projections (e.g., Tebaldi et al., 2006; Gutowski Jr. et al., 2007; Giorgi et al., 2011, 2014a, b; Sillmann et al., 2013b; Pendergrass and Hartmann, 2014).
Clearly, model projections indicate that the characteristics of precipitation are going to be substantially modified by global warming, most likely to a greater extent than mean precipitation itself. Whether these changes are already evident in the observational record is still an open debate. Giorgi et al. (2011, 2014a) found some consistency between model projections and observed trends in different precipitation indices for the period 1976–2005 in a global and some regional observational datasets. Some indications of observed increases in precipitation extremes over different regions of the world have also been highlighted in different IPCC reports (IPCC, 2007, 2013) and, for example, in Fischer and Knutti (2016). In addition, data from the Munich Reinsurance Company suggest an increase in the occurrence of meteorological and climatic catastrophic events, such as flood and drought, since the mid-1980s. However, the large uncertainty and diversity in precipitation observational estimates, most often blending in situ station observations and satellite-derived information using a variety of methods, along with the paucity of data coverage in many regions of the world and the large variability of precipitation, make robust statements on observed trends relatively difficult.
A key issue concerning precipitation projections is the representation of cloud and precipitation processes in climate models. These processes are among the most difficult to simulate because they are integrators of different physical phenomena and, especially for convective precipitation, they occur at scales that are smaller than the resolution of current GCMs and RCMs. For example, the representation of clouds and precipitation is the main contributor to a model's climate sensitivity and the simulation of precipitation statistics is quite sensitive to the use of different cumulus parameterizations (e.g., Flato et al., 2013). In fact, both global and regional climate models have systematic errors in the simulation of precipitation statistics, such as an excessive number of light precipitation events and an underestimate of the intensity of extremes (Kharin et al., 2005; Flato et al., 2013; Sillmann et al., 2013a). These systematic biases are related not only to the relatively coarse model resolution, but also to inadequacies of resolvable scale and convective precipitation parameterizations (e.g., Chen and Knutson, 2008; Wehner et al., 2010; Flato et al., 2013).
Experiments with non-hydrostatic RCMs run at convection-permitting resolutions (1–3 km), in which cumulus convection schemes are not utilized and convection is explicitly resolved with non-hydrostatic wet dynamics, have shown that some characteristics of simulated precipitation are strongly modified compared to coarser-resolution models, most noticeably the precipitation peak hourly intensity and diurnal cycle (e.g., Prein et al., 2015). It is thus possible that some conclusions based on coarse-resolution models might be modified as more extensive experiments at convection-permitting scales, both global and regional, become available.
Despite these difficulties and uncertainties, and given the problems associated with retrieving accurate observed estimates of mean precipitation at continental to global scales, robust changes in different characteristics of precipitation (rather than the mean) may provide the best opportunity to detect and attribute trends in the Earth's hydrological cycle. Moreover, the investigation of the response of precipitation to warming may provide an important tool towards a better understanding and modeling of key hydroclimatic processes, most noticeably tropical convection. The ability to simulate given responses of precipitation characteristics can also provide an important benchmark to evaluate the performance of climate models in describing precipitation and cloud processes. Therefore, as more accurate observational datasets become available, along with higher-resolution and more comprehensive GCM and RCM projections, the understanding of the response of the Earth's hydroclimate to global warming, and its impacts on human societies, will continue to be one of the main research challenges within the global change debate.
CMIP5 data are available at the website http://cmip-pcmdi.llnl.gov/cmip5/data_portal.html (last access: August 2016, Taylor et al., 2012). MED-CORDEX data are available at https://www.medcordex.eu/medcordex.php (last access: April 2015, Ruti et al., 2016) and Euro-CORDEX data at https://euro-cordex.net/index.php.en (last access: February 2016, Jacob et al., 2014).
The supplement related to this article is available online at: https://doi.org/10.5194/esd-10-73-2019-supplement.
FG conceived the paper and contributed to the analysis and writing of the text. FR and EC contributed to the analysis and writing of the text.
The authors declare that they have no conflict of interest.
We thank the CMIP5, MED-CORDEX and EURO-CORDEX
modeling groups for making available the simulation data
used in this work. A good portion of the material presented in this
paper is drawn from the European Geosciences Union (EGU) 2018
Alexander von Humboldt medal lecture delivered by one of the
authors (Filippo Giorgi).
Edited by: Govindasamy Bala
Reviewed by: two anonymous referees
Allan, R. P. and Soden, B. J.: Atmospheric warming and the amplification of precipitation extremes, Science, 321, 1481–1484, 2008.
Anstey, J. A., Davini, P., Grey, L. J., Woollings, T. J., Butchart, N., Cagnazzo, C., Christiansen, B., Hardiman, S. C., Osprey, S. M., and Yang, S.: Multi-model analysis of northern hemisphere winter blocking: Model biases and the role of resolution, J. Geophys. Res.-Atmos., 118, 3956–3971, 2013.
Becker, T., Stevens, B., and Hohenegger, C.: Imprint of the convective parameterization and sea surface temperature on large scale convective self-aggregation, J. Adv. Model Earth Syst., 9, 1488–1505, 2017.
Biasutti, M., Voigt, A., Boos, W. R., Bracconot, P., Hargreaves, J. C., Harrison, S. P., Kang, S. M., Mapes, B. E., Scheff, J., Schumacher, C., Sobel, A. H., and Xie, S.-P.: Global energetics and local physics as drivers of past, present and future monsoons, Nat. Geosci., 11, 392–400, 2018.
Boberg, F., Berg, P., Thejll, P., Gutowski, W. J., and Christensen, J. H.: Improved confidence in climate change projections of precipitation evaluated using daily statistics from the PRUDENCE ensemble, Clim. Dynam., 32, 1097–1106, 2009.
Byrne, M. P., Pendergrass, A. G., Rapp, A. D., and Wodzicki, K. R.: Response of the Intertropical Convergence Zone to Climate Change: Location, Width, and Strength, Curr. Clim. Chang. Reports, 4, 355–370, 2018.
Chen, C. T. and Knutson, T.: On the verification and comparison of extreme rainfall indices from climate models, J. Climate, 21, 1605–1621, 2008.
Chen, D. and Dai, A.: Dependence of estimated precipitaiton frequency and intensity on data resolution, Clim. Dynam., 50, 3625–3647, 2018.
Chou, C., Chen, C.-A., Tan P.-H., and Chen, K. T.: Mechanisms for global warming impacts on precipitation frequency and intensity, J. Climate, 25, 3291–3306, 2012.
Christensen, J. H. and Christensen, O. B.: Climate modeling: Severe summertime flooding in Europe, Nature, 421, 805–806, 2003.
Diffenbaugh, N. S., Giorgi, F., Raymond, L., and Bi, X.: Indicators of 21st century socioclimatic exposure, P. Natl. Acad. Sci. USA, 104, 20195–20198, 2007.
Easterling, D. R., Meehl, G. A., Parmesan, C., Changnon, S. A., and Mearns, L. O.: Climate extremes: Observations, modeling and impacts, Science, 289, 2068–2074, 2000.
Fischer, E. M. and Knutti, R.: Observed heavy precipitation increase confirms theory and early models, Nat. Clim. Change, 6, 986–990, 2016.
Flato, G., Marotzke, J., Abiodun, B., Bracconot, P., Chou, S. C., Collins, W., Cox, P., Driouech, F., Emori, S., Eyring, V., Forest, C., Glecker, P., Guiliard, E., Jacob, C., Kattsov, V., Reason, C., and Rummukainen, M.: Evaluation of climate models. Chapter 9 of Climate Change 2013. The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Dahe, Q., Plattner, G.-K., Tignor, M. M. B., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 741–866, 2013.
Gao, X. J., Pal, J. S., and Giorgi, F.: Projected changes in mean and extreme precipitation over the Mediterranean region from high resolution double nested RCM simulations, Geophys. Res. Lett., 33, L03706, https://doi.org/10.1029/2005GL024954, 2006.
Giorgi, F. and Bi, X.: Regional changes in surface climate interannual variability for the 21st century from ensembles of global model simulations, Geophys. Res. Lett., 32, L13701, https://doi.org/10.1029/2005GL023002, 2005.
Giorgi, F. and Coppola, E.: Projections of 21st century climate over Europe, EPJ Web Conf., 1, 29–46, 2009.
Giorgi, F., Shields Brodeur, C., and Bates, G. T.: Regional climate change scenarios over the United States produced with a nested regional climate model, J. Climate, 7, 375–399, 1994.
Giorgi, F., Jones, C., and Asrar, G.: Addressing climate information needs at the regional level: The CORDEX framework, WMO Bulletin, 58, 175–183, 2009.
Giorgi, F., Im, E.-S., Coppola, E., Diffenbaugh, N. S., Gao, X. J., Mariotti, L., and Shi, Y.: Higher hydroclimatic intensity with global warming, J. Climate, 24, 5309–5324, 2011.
Giorgi, F., Coppola, E., Solmon, F., Mariotti, L., Sylla, M. B., Bi, X., Elguindi, N., Diro, G. T., Nair, V., Giuliani, G., Turuncoglu, U. U., Cozzini, S., Guttler, I., O'Brien, T. A., Tawfik, A. B., Shalaby, A., Zakey, A. S., Steiner, A. L., Stordal, F., Sloan, L. C., and Brankovic, C.: RegCM4: Model description and preliminary tests over multiple CORDEX domains, Clim. Res., 52, 7–29, 2012.
Giorgi, F., Coppola, E., and Raffaele, F.: A consistent picture of the hydroclimatic response to global warming from multiple indices: Modeling and observations, J. Geophys. Res., 119, 11695–11708, 2014a.
Giorgi, F., Coppola, E., Raffaele, F., Diro, G. T., Fuentes-Franco, R., Giuliani, G., Mamgain, A., Llopart-Pereira, M., Mariotti, L., and Torma, C.: Changes in extremes and hydroclimatic regimes in the CREMA ensemble projections, Clim. Change, 125, 39–51, 2014b.
Giorgi, F., Torma, C., Coppola, E., Ban, N., Schar, C., and Somot, S.: Enhanced summer convective rainfall at Alpine high elevations in response to climate warming, Nat. Geosci., 9, 584–589, 2016.
Giorgi, F., Coppola, E., and Raffaele, F.: Threatening levels of cumulative stress due to hydroclimatic extremes in the 21st century, NPJ Climate and Atmospheric Science, 1, 18, https://doi.org/10.1038/s41612-018-0028-6, 2018.
Gutowski Jr., W. J., Takle, E. S., Kozak, K. A., Patton, J. C., Arritt, R. W., and Christensen, J. C.: A possible constraint on regional precipitation intensity changes under global warming, J. Hydrometeorol., 8, 1382–1396, 2007.
Gutowski Jr., W. J., Giorgi, F., Timbal, B., Frigon, A., Jacob, D., Kang, H.-S., Raghavan, K., Lee, B., Lennard, C., Nikulin, G., O'Rourke, E., Rixen, M., Solman, S., Stephenson, T., and Tangang, F.: WCRP COordinated Regional Downscaling EXperiment (CORDEX): a diagnostic MIP for CMIP6, Geosci. Model Dev., 9, 4087–4095, https://doi.org/10.5194/gmd-9-4087-2016, 2016.
Held, I. M. and Soden, B. J.: Robust responses of the hydrological cycle to global warming, J. Climate, 19, 5686–5699, 2006.
Herold, N., Behrangi, A., and Alexander, L. V.: Large uncertainties in observed daily precipitation extremes over land, J. Geophys. Res.-Atmos., 122, 668–681, 2017.
Intergovernmental Panel on Climate Change (IPCC): Climate Change 2007. The Physical Science Basis. Working Group I Contribution to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Solomon, S., Qin, D., Manning, M., Marquis, M., Averyt, K., Tignor, M. M. B., Miller Jr., H. L., and Chen, Z., Cambridge University Press, Cambridge, UK, 996 pp., 2007.
Intergovernmental Panel on Climate Change (IPCC): Managing the risks of extreme events and disasters to advance climate change adaptation, IPCC Special Report, edited by: Field, C. B., Barros, V., Stocker, T. F., Dahe, Q., Dokken, D. J., Ebi, K. L., Mastrandrea, M. D., Mach, K. J., Plattner, G.-K., Allen, S. K., Tignor, M., and Midgley, P. M., Cambridge University Press, Cambridge, UK, 582 pp., 2012.
Intergovernmental Panel on Climate Change (IPCC): Climate Change 2013. The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Dahe, Q., Plattner, G.-K., Tignor, M. M. B., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 1029 pp., 2013.
Ivancic, T. J. and Shaw, S. B.: A U.S. based analysis of the ability of the Clausius-Clapeyron relationship to exaplin changes in extreme rainfall with changing temperature, J. Geophys. Res.-Atmos., 121, 3066–3078, 2016.
Jacob, D., Petersen, J., Eggert, P., Alias, A., Christensen, O. B., Bouwer, L. M., Braun, A., Colette, A., Deque, M., Georgievski, G., Georgopoulou, E., Gobiet, A., Menut, L., Nikulin, G., Haensler, A., Hampelmann, N., Jones, C., Keuler, K., Kovats, S., Kroner, N., Kotlarski, S., Kriegsmann, A., Martin, E., van Meijgaard, E., Moseley, C., Pfeifer, S., Preuschmann, S., Radermacher, C., Radtke, K., Rechid, D., Rounsevell, M., Samuelsson, P., Somot, S., Soussana, J. F., Teichmann, C., Valentini, R., Vautard, R., Weber, B., and Yiou, P.: EURO-CORDEX: New high resolution climate change projections for European impact research, Reg. Environ. Change, 14, 563–578, 2014.
Jones, C., Giorgi, F., and Asrar, G.: The COordinated Regional Downscaling EXperiment: CORDEX. An international downscaling link to CMIP5, CLIVAR Exchanges, 16, 34–40, 2011.
Kharin, V. V., Zwiers, F. W., and Zhang, X.: Intercomparison of near surface temperature and precipitation extremes in AMIP-2 simulations, reanalyses and observations, J. Climate, 18, 5201–5233, 2005.
Lenderink, G. and van Meijgaard, K.: Increase in hourly extreme precipitaiton beyond expectations from temperature change, Nat. Geosci., 1, 511–514, 2008.
Moss, R. H., Edmonds, J. A., Hibbard, K. A., Manning, M. R., Rose, S. K., van Vuuren, D. P., Carter, P. R., Emori, S., Kainuma, M., Kram, T., Meehl, G. A., Mitchell, J. F. B., Nakicenovic, N., Rihai, K., Smith, S. J., Stouffer, R. J., Thompson, A. M., Weyant, J. P., and Willbanks, T. J.: The next generation of scenarios for climate change research and assessment, Nature, 463, 747–756, 2010.
Mueller, C. J. and Held, I. M.: Detailed investigation of the self-aggregation of convection in cloud-resolving simulations, J. Atmos. Sci., 69, 2551–2565, 2012.
Pall, P., Allen, M. R., and Stone, D. A.: Testing the Clausius-Clapeyron constraint on changes in extreme precipitaiton under CO2 warming, Clim. Dynam., 28, 351–363, 2007.
Pendergrass, A. G. and Hartmann, D. L.: Changes in the distribution of rain frequency and intensity in response to global warming, J. Climate, 27, 8372–8383, 2014.
Pendergrass, A. G., Knutti, R., Lehner, F., Deser, C., and Sanderson, B. M.: Precipitation variability increases in a warmer climate, Sci. Rep.-UK, 7, 17966, https://doi.org/10.1038/s41598-017-17966-y, 2017.
Pfahl, S., O'Gorman, P. A., and Fischer, E. M.: Understanding the regional pattern of projected future changes in extreme precipitation, Nat. Clim. Change, 7, 4230427, https://doi.org/10.1038/nclimate3287, 2017.
Power, S., Delage, F., Chung, C., Kociuba, G., and Keay, K.: Robust twenty-first century projections of El-Nino and related precipitation variability, Nature, 502, 541–545, 2013.
Prein, A. F., Langhans, W., Fosser, G., Ferrone, A., Ban, N., Goergen, K., Keller, M., Tolle, M., Gutjahr, O., Feser, F., Brisson, E., Koller, S., Schmidli, J., van Lipzig, N. P. M., and Leung, R.: A review on regional convection-permitting climate modeling: Demonstrations, prospects and challenges, Rev. Geophys., 53, 323–361, 2015.
Raisanen, J.: CO2 – induced changes in interannual temperature and precipitation variability in 19 CMIP2 experiments, J. Climate, 15, 2395–2411, 2002.
Rihai, K., van Vuuren, D. P., Kriegler, E., Edmonds, J., O'Neill, B. C., Fujimori, S., Bauer, N., Calvin, K., Dellink, R., Fricko, O., Luta, W., Popp, A., Cuaresma, J. C., Samir, K. C., Leimbach, M., Jiang, L., Kram, T., and Rao, S.: The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: An Overview, Global Environ. Chang., 42, 153–168, 2016.
Ruti, P., Somot, S., Giorgi, F., Dubois, C., Flaounas, E., Obermann, A., Dell'Aquila, A., Pisacane, A., Harzallah, A., Lombardi, E., Ahrens, B., Akhtar, N., Alias, A., Arsouze, T., Aznar, R., Bastin, S., Bartholy, J., Beranger, K., Beuvier, J., Bouffies-Cloche, S., Brauch, J., Cabos, W., Calmanti, S., Calvet, J. C., Carillo, A., Conte, D., Coppola, E., Djurdjevic, V., Drobinski, P., Elizalde, A., Gaertner, M., Galan, P., Gallardo, C., Goncalves, M., Gualdi, S., Jorba., O., Jorda, G., Lheveder, B., Lebeaupin-Brossier, C., Li, L., Liguori, G., Lionello, P., Macias-Moy, D., Nabat, P., Onol, B., Rajkovic, B., Ramage, K., Sevault, F., Sannino, G., Struglia, M. V., Sanna, A., Torma, G., and Vervatis, V.: MED-CORDEX initiative for Mediterranean climate studies, B. Am. Meteorol. Soc., 97, 1187–1208, 2016.
Schiemann, R., Demory, M.-E., Shaffrey, L. C., Strachan, J., Vidale, P. L., Mizielinski, M. S., Roberts, M. J., Matsueda, M., Wehner, M. F., and Jung, T.: The resolution sensitivity of northern hemisphere blocking in 4 25-km atmospheric global circulation models, J. Climate, 30, 337–358, 2017.
Sedalcek, J. and Knutti, R.: Half of the World's population experience robust changes in the water cycle for a 2C warmer World, Environ. Res. Lett., 9, 044008, https://doi.org/10.1088/1748-9326/9/4/044008, 2014.
Sillmann, J., Kharin, V. V., Zhang, X., Zwiers, F. W., and Bronaugh, D.: Climate extreme indices in the CMIP5 multimodel ensemble. Part I: Model evaluation in the present climate, J. Geophys. Res., 118, 1716–1733, 2013a.
Sillmann, J., Kharin, V. V., Zwiers, F. V., Zhang, X., and Bronaugh, D.: Climate extreme indices in the CMIP5 multimodel ensemble: Part 2. Future climate projections, J. Geophys. Res., 118, 2473–2493, 2013b.
Taylor, K. E., Stouffer, R. J., and Meehl, G. A.: An Overview of CMIP5 and the Experiment Design, B. Am. Meteorol. Soc., 93, 485–498, 2012.
Tebaldi, C., Hayhoe, K., Arblaster, J. M., and Meehl, G. A.: Going to the extremes: An intercomparison of model-simulated historical and future changes in extreme events, Clim. Change, 79, 185–211, 2006.
Thackeray, C. W., DeAngelis, A. M., Hall, A., Swain, D. L., and Qu, X.: On the connection between global hydrologic sensitivity and regional wet extremes, Geophys. Res. Lett., 45, 20, https://doi.org/10.1029/2018GL079698, 2018.
Trenberth, K. E.: Conceptual framework for changes of extremes of the hydrological cycle with climate change, Clim. Change, 42, 327–339, 1999.
Trenberth, K. E.: Changes in precipitation with climate change, Clim. Res., 47, 123–138, 2011.
Trenberth, K. E., Dai, A., Rasmussen, R. M., and Parsons, D. B.: The changing character of precipitation, B. Am. Meteorol. Soc., 84, 1205–1217, 2003.
Trenberth, K. E., Smith, L., Qian, T., Dai, A., and Fasullo, J.: Estimates of the global water budegt and its annual cycle using observational and model data, J. Hydrometeorol., 8, 758–769, 2007.
Warner, T. T.: Numerical Weather and Climate Prediction, Cambridge University Press, Cambridge, UK, 526 pp., 2010.
Wehner, M. F., Smith, R. L., Bala, G., and Duffy, P.: The effect of horizontal resolution on simulaiton of very extreme US precipitation events in a global atmosphere model, Clim. Dynam., 24, 241–247, 2010.