the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Meeting climate targets by direct CO2 injections: what price would the ocean have to pay?
Wolfgang Koeve
David P. Keller
Julia Getzlaff
Andreas Oschlies
We investigate the climate mitigation potential and collateral effects of direct injections of captured CO2 into the deep ocean as a possible means to close the gap between an intermediate CO2 emissions scenario and a specific temperature target, such as the 1.5 ∘C target aimed for by the Paris Agreement. For that purpose, a suite of approaches for controlling the amount of direct CO2 injections at 3000 m water depth are implemented in an Earth system model of intermediate complexity.
Following the representative concentration pathway RCP4.5, which is a medium mitigation CO2 emissions scenario, cumulative CO2 injections required to meet the 1.5 ∘C climate goal are found to be 390 Gt C by the year 2100 and 1562 Gt C at the end of simulations, by the year 3020. The latter includes a cumulative leakage of 602 Gt C that needs to be reinjected in order to sustain the targeted global mean temperature.
CaCO3 sediment and weathering feedbacks reduce the required CO2 injections that comply with the 1.5 ∘C target by about 13 % in 2100 and by about 11 % at the end of the simulation.
With respect to the injection-related impacts we find that average pH values in the surface ocean are increased by about 0.13 to 0.18 units, when compared to the control run. In the model, this results in significant increases in potential coral reef habitats, i.e., the volume of the global upper ocean (0 to 130 m depth) with omega aragonite > 3.4 and ocean temperatures between 21 and 28 ∘C, compared to the control run. The potential benefits in the upper ocean come at the expense of strongly acidified water masses at depth, with maximum pH reductions of about −2.37 units, relative to preindustrial levels, in the vicinity of the injection sites. Overall, this study demonstrates that massive amounts of CO2 would need to be injected into the deep ocean in order to reach and maintain the 1.5 ∘C climate target in a medium mitigation scenario on a millennium timescale, and that there is a trade-off between injection-related reductions in atmospheric CO2 levels accompanied by reduced upper-ocean acidification and adverse effects on deep-ocean chemistry, particularly near the injection sites.
- Article
(2588 KB) -
Supplement
(904 KB) - BibTeX
- EndNote
The Paris Agreement of December 2015 has set the political target of limiting global warming to well below 2 ∘C, if not 1.5 ∘C, above preindustrial levels (UNFCCC, 2015). Staying within the Paris target range is perceived as a safe limit that avoids dangerous anthropogenic climate change and ensures sustainable food production and economic development (Rockström et al., 2009; Knutti et al., 2015; Rogelj et al., 2016). As a first step towards meeting the Paris climate goals, countries have outlined national post-2020 climate action plans by submitting their nationally determined contributions (NDCs) to climate mitigation in order to meet the <2 ∘C climate target (e.g., Clémençon, 2016). However, even if these NDCs are fully realized, it is estimated that a median warming of 2.6 to 3.1 ∘C will occur by the year 2100 (Rogelj et al., 2016). Consequently, it is questionable whether conventional measures currently considered by individual states will be sufficient to reach and maintain the <2 ∘C climate target (e.g., Horton et al., 2016).
The scientific rationale of such claims is based on observational records and results of climate models of varying complexity that have found a tight correlation between cumulative CO2 emissions and global mean temperature (Allen et al., 2009; Matthews et al., 2009; MacDougall, 2016). From this transient climate response to cumulative carbon emissions (TCRE) it can be estimated that the total quota of CO2 emissions from all sources (fossil-fuel combustion, industrial processes and land-use change) that is compatible with a 1.5 ∘C target will be used up in a few years at current emission rates (Knopf et al., 2017; Mengis et al., 2018), and for a 2 ∘C target it is likely to be reached in the next 2 to 3 decades (Friedlingstein et al., 2014). Thus, the window of opportunity for deep and rapid decarbonization that would allow for such a climate target through emission reduction alone is closing soon (Sanderson et al., 2016).
Given the very challenging and urgent nature of the task of reaching the agreed-upon Paris climate goals, unconventional methods are being discussed. Under specific consideration are negative emission technologies, i.e., measures that deliberately remove CO2 from the atmosphere (e.g., Gasser et al., 2015) and store it somewhere else, e.g., in geological reservoirs or the deep ocean (e.g., IPCC, 2005). Negative emissions are already included in all realistic scenarios from integrated assessment models (IAMs) that limit global warming to <2 ∘C or less above preindustrial levels (Collins et al., 2013; Rockström et al., 2016; Rogelj et al., 2016). However, none of the currently debated negative-emissions technologies, such as bioenergy with carbon capture and storage (BECCS), direct air capture with carbon storage (DACCS), and enhanced weathering (EW), appear to have, regardless of the scenario, the potential to meet the <2 ∘C target without significant impacts on land, energy, water or nutrient resources (Fuss et al., 2014; Smith et al., 2016; Williamson, 2016; Boysen et al., 2017).
One other option that has been considered is ocean carbon sequestration by the direct injection of CO2 into the deep ocean (e.g., Marchetti, 1977; Hoffert et al., 1979; Orr et al., 2001; Orr, 2004; IPCC, 2005; Reith et al., 2016). The CO2 could be derived from point sources such as power plants or direct air capture facilities, and thereby it could contribute to the carbon sequestration part of CCS, DACCS or BECCS. The direct injection of CO2 into the deep ocean can also be thought of as the deliberate acceleration of the oceanic uptake of atmospheric CO2, which happens naturally via invasion and dissolution of CO2 into the surface waters, albeit at a relatively slow rate limited by the sluggish ocean overturning circulation. On millennial timescales, about 65 %–80 % of anthropogenic CO2 is thought to be taken up by the ocean via gas exchange at the ocean surface and by entrainment of surface waters into the deep ocean. This portion rises to 73 %–93 % on timescales of tens to hundreds of millennia via the neutralization of carbonic acid with sedimentary calcium carbonate (CaCO3) (e.g., Archer, 2005; Zeebe, 2012). Directly injecting CO2 into the deep ocean could speed up this natural process by directly accessing deep waters, some of which remain isolated from the atmosphere for hundreds or thousands of years (DeVries and Primeau, 2011; their Fig. 12), and by bringing the anthropogenic CO2 in closer contact with the sediment where carbonate compensation reactions occur. This would prevent anthropogenic CO2 from having an effect on the climate in the near future and accelerate its eventual and nearly permanent removal via reactions with CaCO3 sediments.
Despite the well-known potential of the ocean to take up and store carbon (e.g., Sarmiento and Toggweiler, 1984; Volk and Hoffert, 1985; Sabine et al., 2004), direct CO2 injection into the deep ocean is currently not allowed by the London Protocol and the Convention for the Protection of the Marine Environment of the North-East Atlantic (OSPAR Convention) (Leung et al., 2014). A main concern that led to the current ban is that direct CO2 injection will harm marine ecosystems in the deep sea, e.g., cold-water corals and sponge communities, at least close to the injection site (e.g., IPCC, 2005; Schubert et al., 2006; Gehlen et al., 2014). As emphasized by Keeling (2009) and Ridgwell et al. (2011) there are, however, trade-offs between injection-related damages in the deep ocean and benefits at the ocean surface via a reduction in atmospheric pCO2 and a decrease in upper-ocean acidification. These should be discussed in relation to other mitigation options, which probably all imply offsetting some local harm against global benefits. Our current study aims to inform such a debate by providing quantitative information about impacts on ocean carbonate chemistry caused by the direct injection of CO2 into the deep ocean as a potential measure to reach and maintain a specific temperature target as given by the Paris climate targets.
For this purpose, we consider the direct injection of CO2 into the deep ocean as “oceanic CCS”, deposing CO2 from point sources such as fossil-fuel- or biomass-based power plants or direct air capture plants. We assume that aggressive emission reduction has led from a business-as-usual CO2 emission scenario to a world with intermediate CO2 emissions such as the one represented by the Representative Concentration Pathway (RCP) 4.5. Model-predicted global mean surface air temperatures for the RCP4.5 CO2 emission scenario range between 1.7 and 3.2 ∘C for the year 2100 (Clarke et al., 2014), which is approximately in agreement with the warming after the full achievement of current NDCs. Consequently, the 1.5 ∘C climate target would not be reached under the RCP4.5 scenario and is likely to be exceeded after the year 2050 (IPCC, 2014). We here explore the potential as well as collateral oceanic effects of oceanic CCS as a means to fill the gap between emissions and climate impacts of the RCP4.5 and the 1.5 ∘C target of the Paris agreement. Note that we neglect the effects of non-CO2 forcing agents as well as any additional costs and trade-offs in terms of CO2 emissions caused by the carbon capture and injections (e.g., through the implementation of required infrastructure for deploying oceanic CCS). Consequently, our results provide a lower-limit estimate, i.e., the least cumulative CO2 amount that would need to be injected into the deep ocean in order to comply with the desired target. The paper is organized as follows: in Sect. 2 we address the methodological framework by describing the University of Victoria (UVic) model and the experimental setup of our experiments. In Sect. 3 the results and the discussion of our model simulations are presented. Section 4 outlines the conclusions.
2.1 Model description
The model used is version 2.9 of the University of Victoria Earth System Climate Model (UVic ESCM). It consists of three dynamically coupled main components: a three-dimensional general circulation ocean model based on the Modular Ocean Model (MOM2) (Pacanowski, 1996) including a marine biogeochemical model (Keller et al., 2012), a dynamic and thermodynamic sea-ice model (Bitz and Lipscomb, 1999), and a CaCO3 sediment model (Archer, 1996). The UVic ESCM further includes a terrestrial vegetation and carbon-cycle model (Meissner et al., 2003) based on the Hadley Centre TRIFFID (Top-down Representation of Interactive Foliage and Flora Including Dynamics) model and the hydrological land component MOSES (Met Office Surface Exchange Scheme), and a one-layer atmospheric energy–moisture balance model (based on Fanning and Weaver, 1996). All components have a common horizontal resolution of 3.6∘ longitude × 1.8∘ latitude. The oceanic component has 19 vertical levels with thicknesses ranging from 50 m near the surface to 500 m in the deep ocean. Formulations of the air–sea gas exchange and seawater carbonate chemistry are based on the Ocean Carbon-Cycle Model Intercomparison Project (OCMIP) abiotic protocol (Orr et al., 1999). Marine sediment processes of CaCO3 burial and dissolution are simulated using a model of deep-ocean sediment respiration (Archer, 1996).
2.2 Experimental design
For our default control run and injection experiments, the model has been spun up for 10 000 years under preindustrial atmospheric and astronomic boundary conditions and run from 1765 to 2005 using historical fossil-fuel and land-use carbon emissions (Keller et al., 2014). From the year 2006 onwards simulations are forced with CO2 emissions according to the RCP4.5 and the Extended Concentration Pathway (ECP) 4.5, which runs until the year 2500 (Meinshausen et al., 2011). This forcing includes CO2 emissions from fossil-fuel burning as well as land-use carbon emissions, e.g., from deforestation. After the year 2500, CO2 emissions are assumed to decrease linearly until they cease at the end of the simulations in year 3020. In the default control run and injection experiments we neither apply greenhouse gas emissions other than CO2 nor simulate the effect of sulfate aerosols or non-CO2 effects of land-use change. Further, prescribed monthly varying winds from the National Centers for Environmental Prediction (NCEP) reanalysis are used together with dynamic feedback from a 1st-order approximation of geostrophic wind anomalies associated with changing winds in a changing climate (Weaver et al., 2001).
Simulated CO2 injections are based on the OCMIP carbon sequestration protocols (see Orr et al., 2001; Orr, 2004). These are carried out in an idealized manner by adding CO2 directly to the dissolved inorganic carbon (DIC) pool. This neglects gravitational effects, and it also assumes that the injected CO2 instantaneously dissolves into seawater and is transported quickly away from the injection point and is distributed homogenously over the entire model grid box. The lateral dimensions of this are a few hundred kilometers and many tens of meters in the vertical direction (Reith et al., 2016). Consequently, the formation of CO2 plumes or lakes as well as the potential risk of fast-rising CO2 bubbles is neglected (IPCC, 2005; Bigalke et al., 2008).
The physical transport of the injected CO2 and its transport pathways from the individual injection sites towards the surface of the ocean are tracked by means of inert “dye” tracers (one per injection site). At the injections sites, these tracers are loaded at rates proportional to the amount of CO2 injected. At the sea surface the tracers are subject to a loss to the atmosphere, which is computed in proportionality to the total CO2 gas exchange and fractional contribution to the total DIC of the respective tracer at the ocean surface. The sum of tracer loss to the atmosphere from the individual dye tracers provides an estimate of the loss of injected carbon to the atmosphere.
Following Orr et al. (2001), Orr (2004) and Reith et al. (2016) CO2 is injected at seven separate injection sites, which are defined as individual grid boxes near the Bay of Biscay (42.3∘ N, 16.2∘ W), New York (36.9∘ N, 66.6∘ W), Rio de Janeiro (27.9∘ S, 37.8∘ W), San Francisco (31.5∘ N, 131.4∘ W), Tokyo (33.3∘ N, 142.2∘ E), Jakarta (11.7∘ S, 102.6∘ E) and Mumbai (13.5∘ N, 63∘ E) (Reith et al., 2016; their Fig. 1). Injected CO2 is distributed equally among the seven injection sites. Direct CO2 injections are carried out in the vertical grid box ranging from 2580 to 2990 m water depth (hereafter referred to as injection at 3000 m). Compared to shallower injection, this reduces leakage and increases retention time (e.g., Orr et al., 2001; Orr, 2004; Jain and Cao, 2005; Ridgwell et al., 2011; Reith et al., 2016). At this depth, liquid CO2 is denser than seawater, which has the additional advantage that any undissolved droplets would sink to the bottom rather than rise to the surface.

Figure 1Time series of the different default injection experiments, i.e., the A1 simulation (black lines), A2 simulation (red lines) and A3 simulation (blue lines) for (a) cumulative CO2 injections, (b) global mean surface air temperature, relative to preindustrial levels, (c) atmospheric CO2 concentration, (d) cumulative leakage of injected CO2 and (e) required emission reduction.
2.3 Model experiments
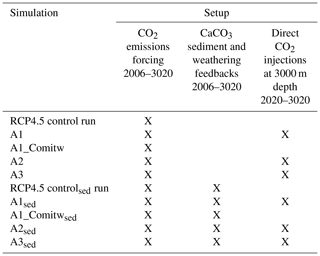
Three conceptually different approaches for applying oceanic CCS are simulated using the UVic model: the first approach (A1) assumes that all anthropogenic CO2 emissions are injected after a warming of 1.5 ∘C is realized for the first time; the second approach (A2) injects, in every year, an amount of CO2 that ensures that temperatures do not rise beyond the 1.5 ∘C target; and the third approach (A3) injects an amount of CO2 to ensure that atmospheric CO2 concentrations follow the RCP/ECP2.6 scenario as closely as possible. All idealized approaches are designed to counter the excessive emissions of the RCP4.5 scenario by direct CO2 injections into the deep ocean to reach and maintain a specific temperature target as given by the 1.5 ∘C target until the end of this century and for another millennium. Injections in A2 (A3) are interrupted when the simulated annual mean surface air temperature (atmospheric pCO2) falls below the respective climate target. We further study how the simulation of CaCO3 sediment feedbacks and associated continental weathering modifies required CO2 injections, and the resulting impacts on ocean biogeochemistry are also studied. Table 1 provides an overview of all conducted simulations and their setup from the year 2006 onwards.
Table 1Overview of all conducted simulations and their setup. The “X” denotes that the respective feature is applied. Note that the applied CO2 forcing follows the RCP4.5 CO2 emission scenario from 2006 to 2100 and the extended RCP4.5 CO2 emissions scenario from 2100 to 2500. From 2500 onwards CO2 emissions linearly decline until 0 Gt C yr−1 in the year 3020.
In the first approach (A1), all further CO2 emissions of the RCP4.5 scenario are completely redirected to the injection sites after the global mean surface air temperature has exceeded the 1.5 ∘C target for the first time. Some committed warming (e.g., Matthews and Caldeira, 2008; Gillet et al., 2011) occurs in these simulations due to past emissions and climate cycle feedbacks. This committed warming is at some point overlaid by the leakage of injected CO2 out of the ocean (e.g., Orr, 2004; Reith et al., 2016) as well as by oceanic and terrestrial carbon-cycle feedbacks that lead to a CO2 increase in the atmosphere and respective additional warming (see Sect. 3.1). To diagnose the contribution from leakage, we design a leakage-free sensitivity simulation (A1_Comitw), in which CO2 emissions are set to zero once the 1.5 ∘C target is reached, and no CO2 is injected into the deep ocean.
In contrast to the first approach, the second one (A2) keeps the global mean temperature at the defined threshold of 1.5 ∘C, relative to preindustrial levels, by injecting as much CO2 into the deep ocean as is necessary to maintain an annual mean temperature that is only 1.5 ∘C above preindustrial levels. We diagnose this amount of CO2 using the transient response to emissions (TCRE, Allen et al., 2009; Matthews et al., 2009; MacDougall, 2016) of our model and the difference of the modeled annual mean atmospheric temperature and the target temperature. CO2 is only injected if the modeled temperature is above the target temperature. In order to avoid interference with seasonal and longer periodic fluctuations of the atmospheric temperature (sensitivity experiments; not shown), we apply a running-mean-averaging timescale of 1000 d. CO2 injection rates required to reach the respective target are updated every 5 d, which is when the atmospheric and oceanic model components are coupled. The rate of CO2 injection taken out of the atmosphere can be larger than the actual CO2 emissions (RCP/ECP4.5), i.e., constituting net negative CO2 emissions.
In the third approach (A3), we inject the amount of CO2 that is needed to follow the atmospheric CO2 concentrations of the extended Representative Concentration Pathway RCP2.6 and Extended Concentration Pathway ECP2.6, which is a reference scenario that has been suggested to reach the <2 ∘C climate target with a ≥66 % probability (IPCC, 2014). From the year 2500 onwards, the targeted atmospheric CO2 concentration is held constant until the end of the simulations. Therefore, at every atmospheric time step the model computes the difference between its currently simulated atmospheric CO2 concentration, given the RCP4.5 CO2 emissions, and the targeted atmospheric CO2 concentration from the RCP2.6 pathway. This difference is used to diagnose the CO2 injection needed to keep the model's atmospheric CO2 concentrations as close as possible to the RCP2.6 concentration pathway. A respective amount of CO2 is injected and subtracted from the prescribed CO2 emissions to the atmosphere, which eventually results in net negative emissions. We apply temporal averaging and update the required CO2 injection every 5 d.
In sensitivity experiments (Table 1) we further investigate the effect of CaCO3 sediment feedbacks and continental weathering on the cumulative CO2 injections and on seawater carbonate chemistry for the different approaches. The effect of CaCO3 sediment dissolution is thought to be relevant as CO2 injected at depth may react relatively directly with sedimentary CaCO3 and increase CaCO3 dissolution near or downstream of the injection sites, resulting in an accelerated neutralization of this anthropogenic CO2 compared to a situation where CO2 slowly invades the ocean via air–sea gas exchange (Archer et al., 1998; IPCC, 2005). Therefore, we investigate the effect of CaCO3 sediment feedbacks in our simulations by running the model with and without a sediment sub-model. The global average percentage of CaCO3 in sediments in our “sed” simulations (Sect. 3.2) is about 31 % for the year 2020 and compares well to about 34.5 % derived from observations as reported in Eby et al. (2009). To ensure that in a steady state (i.e., during the model spin-up) DIC and alkalinity are conserved, the UVic model with the sediment module also has a simple representation of continental weathering to compensate for the burial-related loss of DIC and alkalinity. From the model spin-up we diagnose the global terrestrial weathering flux of DIC as 0.12 Gt C yr−1 with an alkalinity flux of 0.02 Pmol yr−1. During the transient runs with the sediment module, this weathering flux is held constant, whereas sedimentary CaCO3 accumulation or dissolution is allowed to evolve freely. Consequently, ocean alkalinity and DIC are adjusted in response to interactions between seawater, injected CO2 and sediments. Simulations with the sediment and weathering sub-model are based on a separate set of spin-up experiments (50 000 years), drift runs and historical simulations that all employ the sediment and weathering sub-model. Hereafter, simulations performed with the sediment and weathering model are referred to by the subscript sed (Table 1).
Relevant carbonate system parameters that are not computed at the model's run-time are derived offline for all simulations by means of the MATLAB version of CO2SYS (Lewis and Wallace, 1998; van Heuven et al., 2009; Koeve and Oschlies, 2012; currently available from http://cdiac.ess-dive.lbl.gov/ftp/co2sys, last access: 17 November 2017), using carbonic acid dissociation constants of Mehrbach et al. (1973), as refitted by Dickson and Millero (1987), and other related thermodynamic constants (Millero, 1995).
3.1 Oceanic CCS and the 1.5 ∘C climate target
Here, we present the cumulative mass of CO2 injected in the default runs (without CaCO3 sediments) of the different approaches and show how effective these are in reaching and maintaining the 1.5 ∘C climate target.
In the default simulation of the first approach (A1) oceanic CCS starts in the year 2045 after the 1.5 ∘C climate target has been exceeded for the first time at a corresponding atmospheric CO2 concentration of about 466 ppmv (Fig. 1a–c). Between the years 2020 and 2045, about 278 Gt C has been emitted in the form of CO2 into the atmosphere, i.e., a small fraction of the 1242 Gt C of total emissions corresponding to the extended RCP4.5 scenario between the years 2020 and 3020. From 2045 until 3020, all CO2 emissions (964 Gt C in total) are directly injected into the deep ocean (Fig. 1a), resulting in zero anthropogenic CO2 emissions into the atmosphere for the remaining simulation. After the injection starts in the year 2045, the atmospheric CO2 concentration decreases, but this is only until the year 2341, when a minimum of about 409 ppmv is reached (Fig. 1c). The increase of atmospheric CO2 from year 2342 onwards is a result of an earlier leakage of CO2 injected into the deep ocean. By the end of the simulation, a total amount of 437 Gt C has leaked back into the atmosphere (Fig. 1d). Thus, only about 55 % of the total mass injected (964 Gt C) remains in the ocean until the year 3020. From 2078 onwards, the land perennially turns into a carbon source with a total carbon loss of about 21 Gt C to the atmosphere.
Global mean temperature, relative to preindustrial levels, oscillates around the 1.5 ∘C climate target within ±0.02 ∘C after injections started until the year 2200. Until then, this approach (A1) is thus nearly successful in reaching and maintaining the 1.5 ∘C climate target. Subsequently, however, global mean surface air temperature shows a slow increase of up to 0.02 ∘C until 2341 although atmospheric CO2 is still decreasing. This warming signal is owed to the lagged response of the deep ocean to previously increasing atmospheric CO2, i.e., committed warming, resulting in a decline of the ocean heat uptake from the atmosphere and thus in an increase of the global mean temperature (Zickfeldt and Herrington, 2015; Zickfeldt et al., 2016). In this simulation (A1), this feedback mechanism (see also Fig. S1 in the Supplement) is overlaid by increasing an leakage of injected CO2 back into the atmosphere, which becomes the dominating process for atmospheric warming as obvious from the atmospheric CO2 increase after the year 2342 (Fig. 1c and d). Hence, the global mean air temperature shows a steeper increase until it reaches a maximum of about +2.2 ∘C above the preindustrial level at the end of the simulation (Fig. 1b). Thus, on a millennial timescale, the A1 simulation overshoots the 1.5 ∘C climate target by about 0.7 ∘C. By subtracting this diagnosed leakage of 437 Gt C from the cumulative CO2 injections (964 Gt C), we determine the required CO2 emission reduction (527 Gt C) (Fig. 1e) relative to the RCP/ECP4.5 scenario to comply with a global mean temperature of about +2.2 ∘C, relative to preindustrial levels, on a 1000-year timescale.
Oceanic CCS in the second approach (A2) starts as well in 2045 (Fig. 1a and c). Global mean temperature oscillates around the 1.5 ∘C climate target until the year 2300 (Fig. 1b). These oscillations get smaller over time until the global mean temperature essentially stays at 1.5 ∘C until the end of the simulation. We find that the oscillations arise in the applied model from climate–sea-ice feedbacks under the near-term 1.5 ∘C conditions (see Fig. S2). The terrestrial biosphere turns into a carbon source in 2061 and land–atmosphere carbon fluxes oscillate around zero until the end of the simulation. The total carbon loss from land to the atmosphere is about 75 Gt C. Atmospheric CO2 concentrations show a continuous decline when the global mean temperature is held at the aspired climate target (Fig. 1b and c). This is caused by a decline in ocean heat uptake as mentioned above and is consistent with an additional accumulation of heat in the atmosphere at constant atmospheric CO2 concentrations (e.g., Zickfeldt and Herrington, 2015; Zickfeldt et al., 2016). In our second approach, this needs to be counteracted by further CO2 injections into the deep ocean.
By the end of the A2 run, cumulative CO2 injections amount to about 1562 Gt C, which is about 600 Gt C (62 %) higher than in the A1 simulation. This amount of additional CO2 injections is needed in order to reduce global mean warming at the end of the 1000-year simulation from 2.2 ∘C in A1 to 1.5 ∘C in A2. In the A2 run, the diagnosed mass of injected CO2 that has leaked into the atmosphere and has been reinjected into the deep ocean during the entire simulation adds up to about 60 Gt C until the year 3020 (Fig. 1d). Hence, about 61 % of the total mass injected (1562 Gt C) stays in the ocean. This results in a required CO2 emission reduction of about 955 Gt C (Fig. 1e), i.e., the amount of emission reduction necessary to comply with the 1.5 ∘C climate target on a 1000-year timescale.
In the third approach, A3, oceanic CCS starts in the year 2031 (Fig. 1a) as the atmospheric CO2 concentration caused by the RCP4.5 CO2 emission scenario starts to exceed the targeted RCP2.6 atmospheric CO2 concentration. Relative to preindustrial levels, the global mean temperature continues to increase to a maximum of approximately +1.5 ∘C in the year 2078 at a corresponding atmospheric CO2 concentration of 433 ppmv (Fig. 1b and c). Subsequently, the temperature decreases until it reaches about +0.9 ∘C relative to preindustrial temperatures, while the atmospheric CO2 concentration reaches 327 ppmv at the end of the simulation (Fig. 1b and c). Up to that point in time, cumulative CO2 injections in the A3 simulation amount to about 2200 Gt C (Fig. 1a). In response to negative emissions the land turns into an atmospheric carbon source (Keller et al., 2018) between 2076 and 2600 with a total loss of about 144 Gt C to the atmosphere. From the year 2600 onwards, the carbon flux between the atmosphere and land is nearly zero (below 0.03 Gt C yr−1). By the end of the simulation, the diagnosed leakage of injected carbon adds up to about 900 Gt C (Fig. 1d), which means that about 59 % of the injected CO2 remains in the ocean until the year 3020. The required emission reduction to move from an RCP4.5 pathway to RCP2.6 in the A3 run is about 1300 Gt C (Fig. 1e).
By the end of the A3 simulation, cumulative CO2 injections are about 636 Gt C (29 %) higher than in the A2 simulation. This is also reflected in the higher diagnosed leakage by about 293 Gt C in total, when compared to the A2 simulation. In an attempt to follow the atmospheric CO2 concentration of the RCP2.6 (Sect. 2.3), cumulative CO2 injections are almost twice the amount of the cumulative CO2 emissions difference between the RCP4.5 scenario and the RCP2.6 scenario applied here. This can be explained by the fact that deep-oceanic CCS steepens the surface-to-deep DIC gradient (Fig. S3a) fostering a back transport to the surface ocean. Most of this enhanced deep water DIC is transported with the meridional overturning circulation to the Southern Ocean (south of 40∘ S), where the largest fraction of the total leakage occurs in our injection experiments (Fig. S3b). By the end of the A1 simulation, we find that about 60 % of the diagnosed leakage has outgassed in the Southern Ocean compared to about 77 % in the A2 run and about 80 % in the A3 simulation. Overall, we find that the higher the direct CO2 injections into the deep ocean are, the higher the leakage (Fig. 1a and d) is and the higher the relative portion outgassed in the Southern Ocean is.
What this means in terms of the effectiveness of oceanic CCS is further highlighted by the comparison of the required cumulative CO2 injections of the three different approaches (A1, A2 and A3) and the respective required emission reductions needed to reach the run's specific climate target under a RCP/ECP4.5 CO2 emission scenario. As illustrated in Fig. 2a–c, the approaches A1, A2 and A3 represent increasingly stringent climate targets as evident from decreasing atmospheric warming relative to preindustrial conditions. Cumulative CO2 injections by the year 2100 are largely equivalent to the required emission reduction because only a tiny fraction of injected CO2 has outgassed until that point in time (Figs. 1d and 2a). However, by the end of the millennial injection experiments, cumulative CO2 injections are much larger than the required emission reductions in the year 3020 as indicated by the slopes of the eye-fitted lines in Fig. 2b and c. This is due to the fact that the leakage in the injection experiments (Fig. 1d) requires a larger CO2 removal effort; i.e., CO2 that leaks out has to be reinjected. If there were no leakage of injected carbon, i.e., perfect storage, then the cumulative CO2 injections would equal the required emission reductions.
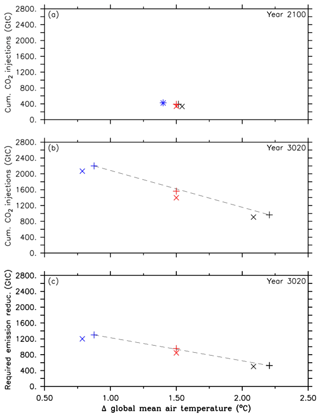
Figure 2Comparison between simulations of the first approach (A1, black symbols), simulations of the second approach (A2, red symbols) and simulations of the third approach (A3, blue symbols). The cross symbols refer to the default simulations, and the X symbols denote simulations with CaCO3 sediment and weathering feedbacks. These symbols represent (a) cumulative CO2 injections and their corresponding global mean temperatures, relative to preindustrial levels, in the year 2100, (b) cumulative CO2 injections and their corresponding global mean temperatures, relative to preindustrial levels, at the end of the simulation (in the year 3020), and (c) required emission reduction and its corresponding global mean temperature, relative to preindustrial levels, at the end of the simulations. Note that the dashed black lines are eye-fitted to the results of the standard runs.
Land response
Biological processes primarily control the exchange of atmospheric CO2 with the land, where the majority of the carbon is stored in soils and permafrost. CO2 is removed from the atmosphere by plant photosynthesis and primarily returned to the atmosphere by respiration and other processes such as fire (Ciais et al., 2013). As long as primary production (GPP; i.e., gross photosynthetic carbon fixation) is greater than carbon losses due to respiration and processes such as fire, the land will be a carbon sink (Le Quéré et al., 2016). If this balance changes, then the land can become a source of CO2 to the atmosphere. In our simulations as emissions increase and decrease (with oceanic CCS), eventually reaching net negative – and/or zero – emissions, the terrestrial carbon cycle is perturbed and can switch from a sink to a source. The magnitude of the land carbon-cycle response due to an injection-related atmospheric carbon reduction, and an eventual increase as in the A1 experiment (see Sect. 3.1), is mainly governed by the reduced CO2 fertilization effect on net primary productivity and the temperature-related change in heterotrophic soil respiration, responses that were investigated in Reith et al. (2016). In all simulations the land changes from a carbon sink to source, eventually reaching almost a balance (almost zero net flux) in the A2 and A3 simulations. In the A1 simulation, the increase in atmospheric CO2 after a period of decline (Fig. 1c) is not able to overcome the temperature effect that elevates respiration rates, and the land continues to perennially lose carbon.
3.2 Sensitivities to CaCO3 sediment feedbacks and weathering fluxes
As illustrated in Fig. 2b, cumulative CO2 injections in the A2sed simulation are about 165 Gt C (11 %) smaller until the year 3020 when compared to the A2 run (1562 Gt C). This smaller CO2 injection is a result of two processes (CaCO3 sediment dissolution and constant terrestrial weathering), which both have the net effect of adding alkalinity to the model ocean when compared to the standard experiments without sediment feedbacks and continuous weathering fluxes. By the end of the simulation, average ocean alkalinity has increased by 32 mmol m−3 in the A2sed run compared to an average value of 2422 mmol m−3 in the A2 run. About 84 % of this increase in global mean alkalinity can be attributed to ocean CCS and resulting sediment dissolution at depth; the rest is from ocean-acidification-induced CaCO3 dissolution according to the RCP4.5 CO2 emission scenario, as evident from the control run with sediment and weathering feedback. An increase in ocean alkalinity may enhance the oceanic uptake of atmospheric CO2, however, only if waters with increased alkalinity arrive at the surface waters and lower surface ocean pCO2. This, in turn, reduces the required CO2 injections to reach and maintain the 1.5 ∘C climate target. Dissolution of CaCO3 deep-sea sediments caused by the injection of CO2 into the deep ocean at 3000 m causes the dissolution of 11.8 Pmol CaCO3 in the A2sed simulation by the year 3020, releasing 11.8 Pmol DIC and 23.6 Pmol alkalinity to the deep ocean. Highest CaCO3 dissolution rates occur in the vicinity of the seven injection sites (Fig. S4a and b). Hence, ocean acidification reaching the deep ocean and ocean CCS convert sediments from a CaCO3 sink (116 Gt CaCO3-C at the end of the respective spin-up run) to a source of its dissolution products. A second process that contributes to the increase in ocean alkalinity is the terrestrial CaCO3 weathering flux, which arrives in the surface ocean via river discharge and amounts to about 19.3 Pmol alkalinity and 9.7 Pmol C (116 Gt C) by the end of the A2sed simulation.
Disentangling the relative role of the two processes (turning CaCO3 burial into CaCO3 dissolution and the continuous flux of alkalinity from terrestrial weathering) with respect to stabilizing oceanic CO2 uptake and thereby affecting the required CO2 injections is not trivial. Waters affected by CaCO3 sediment dissolution in the deep ocean need to return to the ocean surface before having an effect on surface ocean pCO2 and oceanic CO2 uptake (Cao et al., 2009). The fluxes from terrestrial weathering, however, are in our simulation, continuous and constant with time (no sensitivity to weathering changes in atmospheric pCO2, surface air temperature, precipitation or terrestrial production) and directly arrive in the surface ocean via river inflow. It is thus likely that, in comparison to the standard experiments without terrestrial weathering, the latter affects the atmosphere–ocean CO2 flux well before the alkalinity input related to CaCO3 dissolution. Quantifying the effect of each process to reduce the required CO2 injection individually, however, would require additional simulations, e.g., experiments with CaCO3 dissolution turned on but terrestrial weathering turned off. This is beyond the scope of this study. As a consequence of the two processes mentioned above, the required emission reduction amounts to about 846 Gt C, i.e., ∼109 Gt C (11 %) less when compared to the A2 run (Fig. 2b).
The net effects of sediment and weathering feedbacks on the required CO2 injections in simulations of the second approach described above are as well represented in the injection experiments of the first and third approach, but they are of a smaller magnitude, i.e., 5 % less (Fig. 2a–c).
3.3 Biogeochemical impacts
Here, we present injection-related biogeochemical impacts with respect to changes in pH and the saturation state of aragonite in the default simulations of the second (A2) and third approach (A3) and of the respective RCP4.5 control run. Simulations of the first approach are neglected here because this one cannot reach and maintain the 1.5 ∘C climate target.
At the beginning of our default simulations (in the year 2020), the uptake of anthropogenic CO2 has lowered average pH at the ocean surface by about 0.12 units, relative to its preindustrial value of about 8.16 (Fig. 3a). This trend continues in the control simulation until its maximum reduction of about −0.25 units in the year 2762, which stays nearly constant until the end of the simulation (Fig. 3a).
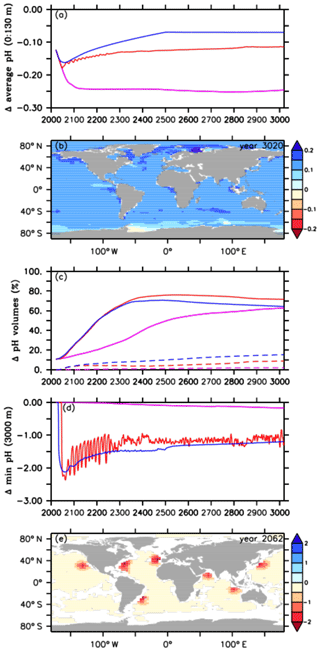
Figure 3Comparison of pH values between the default RCP4.5 control run (purple lines), the A2 simulation (red lines), and the A3 simulation (blue lines) for (a) the average ocean surface pH (0 to 130 m depth), (b) the difference in ocean surface pH, relative to preindustrial levels, between the A2 simulation and the default RCP4.5 control run in the year 3020, (c) pH volumes of the first (≤7.8 and ≥7.4, solid lines) and second categories (<7.4, dashed lines), (d) minimum pH values at 3000 m depth, and (e) the difference in minimum pH at 3000 m depth between the A2 simulation and the default RCP4.5 control run in the year 2062.
As direct CO2 injections lead to a decline in the atmospheric CO2 concentration (Fig. 1c) and, in consequence, to a lower upper-ocean carbon uptake via air–sea gas exchange, we find smaller reductions in the average ocean surface pH, i.e., reduced upper-ocean acidification, after the year 2045 in the A2 simulation and after the year 2031 in the A3 run (Fig. 3a), i.e., shortly after their respective oceanic CCS starting points (Fig. 1a). In the year 3020 the average ocean surface pH in the A2 simulation is about +0.13 units higher, when compared to the control run (Fig. 3a). Using global mean surface ocean pH as a metric, surface ocean acidification in the year 3020 compared to the year 2020 is slightly more intense in the A2 simulation but even more reduced in the A3 run. In both cases this is a direct effect of a lower atmospheric pCO2 (Fig. 1c) compared to the year 2020. Amelioration of surface ocean pH shows regional variability (Fig. 3b), with local maxima of the pH difference between the A2 simulation and the control run in the year 3020 up to +0.23 units, in particular in northern latitudes (Fig. 3b). However, surface ocean acidification is less reduced in the Southern Ocean and even slightly higher in parts of the Weddell Sea, where most of the injected CO2 leaks back into the atmosphere (Fig. 3b).
The simulated ameliorations in the surface ocean pH come at the expense of strongly acidified water masses in the vicinity of the seven injection sites at 3000 m depth, when compared to the RCP4.5 control run. In order to assess how much of the global ocean volume ( km3) shifts to biotically critical pH values in our simulations, we define two pH categories. The first category is defined as 7.4 ≤ pH ≤ 7.8 (solid lines in Fig. 3c) and is chosen because studies have shown that all calcifiers such as coralline algae and foraminiferans are strongly reduced or are absent from acidified areas (pH < 7.8), and the overall biomass of the benthic community is about 30 % less compared to normal conditions (e.g., IPCC, 2011; Fabricius et al., 2015). The second category includes pH values that are lower than 7.4 (dashed lines in Fig. 3c). Such low pH values are for instance found in the vicinity of volcanic CO2 vents and cause a massive drop in biodiversity (e.g., Ogden, 2013).
In our control simulation, we find a steady increase in the ocean volume characterized by 7.4 ≤ pH ≤ 7.8, from about 11 % of total ocean volume in the year 2020 to about 63 % in the year 3020 (Fig. 3c). Oceanic CCS in the A2 and A3 simulation leads to a much steeper increase of “moderately” acidified waters (7.4 ≤ pH ≤ 7.8) with maximum values of 76 % and 71 %, respectively, in the year 2551 (Fig. 3c), but these decrease to 72 % and 64 % in the year 3020. Considering our chosen category (7.4 ≤ pH ≤ 7.8), ocean CCS mainly speeds up interior-ocean acidification but does not increase the acidified volume at the end of the simulation very much. At the end of the simulation the A3 simulation and the A2 run show an increase of affected interior-ocean water by 1 % and 13 %, respectively, compared to the control run.
Respective volumes of the second category (pH < 7.4) start to appear around the year 2400 in the control simulation and then slowly increase to about 2 % until the end of the simulation (Fig. 3e). In contrast, oceanic CCS directly results in the immediate appearance of waters with pH < 7.4, with a volume steadily increasing until the year 3020, where it reaches 9 % of total ocean volume in the A2 simulation and 15 % in the A3 run (Fig. 3c). The differences in both pH categories between the injection experiments are due to the higher cumulative mass of injected CO2 in the A3 run, leading to a smaller volume in the first category and to a bigger volume in the second one (Figs. 1a and 2b).
In order to further identify extreme pH values related to the injections, we look at minimum pH values. These are found at 3000 m depth, i.e., the depth at which oceanic CCS is carried out. Relative to preindustrial conditions, the highest reductions in pH minima are found in the A2 simulation with about −2.37 units in the year 2062, however with large regional variability (Fig. 3d and e). Subsequently, the pH minima in the A2 simulation show strong oscillations until about the year 2400, which are caused by the different annual CO2 injection rates. By the end of the A2 simulation, minimum pH values at 3000 m depth are up to 1 unit lower than in the control run (Fig. 3d). We find a similar pattern in the A3 simulation, although the pH reductions show only slight oscillations, resulting in a more constant pH reduction than in the A2 simulation (Fig. 3d). In comparison to the injection experiments, minimum pH values in the control run start to appear from the year 2300 onwards, leading to a reduction by about −0.17 units in the year 3020 (Fig. 3d); i.e., the deep ocean feels ocean acidification very slowly.
To summarize we observe an increasing benefit in reduced acidification at the ocean surface with higher cumulative CO2 injections, which comes at the expense of increasing acidified water masses in the intermediate and deep ocean, with the strongest pH reductions in the vicinity of the injection sites (Fig. 3e). Figure 4a and b illustrate this trade-off for the injection experiments of the A2 and A3 simulations as well as for the respective control runs in the year 3020. By comparing the different simulations with each other, we find that continental weathering and CaCO3 sediment feedbacks lead to a slightly higher increase in average pH levels at the ocean surface as well as smaller minimum pH values at 3000 m depth, when compared to preindustrial levels. This is caused by the dissolution of CaCO3 sediments and the terrestrial weathering flux, which both have the net effect of adding alkalinity to the ocean and thereby increasing the buffer capacity of seawater.
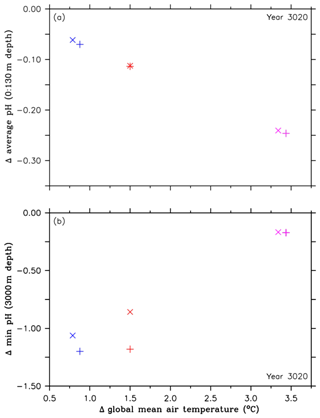
Figure 4Comparison of pH values and their corresponding global mean temperatures in the year 3020, both relative to preindustrial levels, between the RCP4.5 control simulations (purple symbols), simulations of the second approach (A2, red symbols), and simulations of the third approach (A3, blue symbols). The cross symbols refer to the default simulations, and the X symbols denote simulations with CaCO3 sediment and weathering feedbacks. These symbols represent (a) changes in the ocean surface pH (0 to 130 m depth), relative to preindustrial levels, and (b) changes in minimum pH values at 3000 m depth, relative to preindustrial levels.
The reported reductions in global average surface pH in our control simulation caused by the partial oceanic uptake of the RCP4.5 CO2 emissions correspond to an increase in hydrogen ions (H+), which partly react with carbonate ions () to form bicarbonate ions (). This leads in consequence to a reduction in the surface saturation state (Ω) with respect to the CaCO3 minerals aragonite and calcite. This is of importance to marine calcifiers because the formation of shells and skeletons generally occurs where Ω>1 and dissolution occurs where Ω<1 (unless the shells or skeletons are protected, for instance, by organic coatings) (Doney et al., 2009; Guinotte and Fabry, 2008). Since aragonite is about 1.5 times more soluble than calcite (Mucci, 1983) and since aragonite is the mineral form of coral reefs, which are of large socioeconomic value, we only report here on simulated changes in the saturation state of aragonite.
To investigate how tropical coral reef habitats might be impacted in our simulations, we here define the potential coral reef habitat as the volume of the global upper ocean (0–130 m, the two topmost model grid cells), which is characterized by ΩAR>3.4 and ocean temperatures between 21 and 28 ∘C, where most coral reefs exist (Kleypas et al., 1999). We present this volume as the percent fraction of the total upper-ocean volume (4.637×107 km3) in our model.
For preindustrial conditions (in the year 1765), we find that about 37 % of the upper-ocean volume is within our defined thresholds (green star in Fig. 5a and b). At the beginning of our simulations (in the year 2020), this coral reef habitat volume has already declined to about 13 %, consistent with the current observation that many coral reefs are already under severe stress (e.g., Pandolfi et al., 2011; Ricke et al., 2013). In the RCP4.5 control run, we observe that the potential tropical coral reef habitat volume reaches 0 % in the year 2056 and remains so thereafter (Fig. 5a) with a decrease in aragonite oversaturation levels being the main driver.
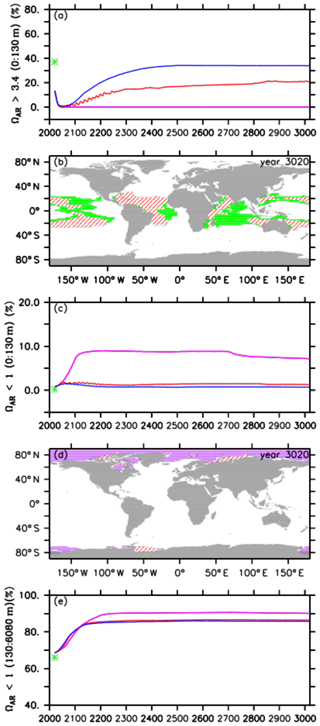
Figure 5Comparison of volumes for different saturation states between preindustrial levels (green stars), the default RCP4.5 control run (purple lines), the A2 simulation (red lines), and the A3 simulation (blue lines) for (a) omega aragonite > 3.4 in the upper ocean (0 to 130 m depth), (b) potential coral reef habitat defined as the volume of the global upper ocean (0 to 130 m depth) with omega aragonite > 3.4 and ocean temperatures between 21 and 28 ∘C for preindustrial levels (green) and the A2 simulation (red hatching) in the year 3020, (c) omega aragonite < 1 in the upper ocean (0 to 130 m depth), (d) the global distribution of omega aragonite < 1 for the default control run (purple) and the A2 simulation (red hatching), and (e) omega aragonite < 1 in the intermediate and deep ocean (130 to 6080 m depth).
In our injection experiments, we find an increase in the potential tropical coral reef habitat volume right after the start of oceanic CCS (Fig. 5a). Despite this, in the A2 simulation the respective volume still approaches zero (0.2 %) in the year 2044, although it does then steadily increase again until it reaches 21 % at the end of the simulation, i.e., still 16 % less than its preindustrial state but also 8 % more compared to the current situation (Fig. 5a and b). The respective habitat volume in the A3 simulation shows an earlier and stronger increase, resulting in a habitat volume of about 34 %, i.e., 3 % less than preindustrial levels, at the end of the model experiment (Fig. 5a).
In preindustrial times, water masses in the upper ocean (0–130 m) that were undersaturated with respect to aragonite (ΩAR<1) were negligible (0.2 %; Fig. 5c, green star). This undersaturated volume has increased to about 1 % at the beginning of our simulations. Over the course of the control run, we observe an increase with a maximum of about 9 % in the year 2212. Subsequently, the respective undersaturated volume slightly decreases until it reaches a minimum of about 7 % at the end of the simulation. Undersaturated surface waters are located in higher latitudes (Fig. 5d), which is, for instance, considered a threat to pteropods like Limacina helicina (e.g., Lischka et al., 2011). In the A2 and A3 simulations, the respective undersaturated volumes are significantly smaller and never exceed 2 % of the surface ocean volume (Fig. 5c and d). Undersaturated surface water volumes in the A2 run are slightly higher than those in the A3 simulation.
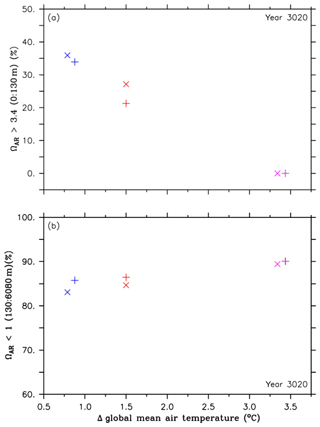
Figure 6Comparison of volumes for different aragonite saturation states and their corresponding global mean temperatures in the year 3020, both relative to preindustrial levels, between the RCP4.5 control simulations (purple symbols), simulations of the second approach (A2, red symbols) and simulations of the third approach (A3, blue symbols). The cross symbols refer to the default simulations, and the X symbols denote simulations with CaCO3 sediment and weathering feedbacks. These symbols represent (a) omega aragonite > 3.4 in the upper ocean (0 to 130 m depth), relative to preindustrial levels, and (b) changes in minimum pH values at 3000 m depth, relative to preindustrial levels.
Further, we assess the volume that is undersaturated with respect to aragonite in the intermediate and deep ocean (130–6080 m) and present it as a percentage of the entire interior-ocean volume (1.311×109 km3). This is of interest since changes in interior-ocean ΩAR may affect the growth conditions of cold-water corals (e.g., Guinotte and Fabry, 2008; Flögel et al., 2014; Roberts and Cairns, 2014) and the dissolution depth of sinking aragonite particles.
At the beginning of the simulations, 69 % of the interior oceans are undersaturated with respect to aragonite, which is about 3 % more than preindustrial levels (Fig. 5e). Subsequently, the increase in undersaturated water volume is similar among all simulations until about the year 2122, when the undersaturated volume in the control simulation continues to increase until its maximum of about 91 % in the year 2713. The undersaturated volumes in the injection experiments show only a very small increase after the year 2122, leading until the year 3020 to values of about 86 % in both injection simulations (Fig. 5e). The bigger volume in the control run is likely caused by acidified waters at the ocean surface that ventilate intermediate and mode waters (Resplandy et al., 2013).
Figure 6a and b show a similar trade-off in the injection experiments of the second and third approach in the year 3020 regarding pH (Fig. 4a and b), i.e., an increase of the aragonite saturation states in the upper ocean and an increase of undersaturated conditions in the intermediate and deep ocean. Further, the effects of CaCO3 sediment dissolution and continental weathering lead to the highest benefit in the upper ocean and the lowest harm in the intermediate and deep ocean (Fig. 6a and b). See Sect. 1 and Figs. S5–S9 about the different evolution of the aragonite saturation horizon (ΩAR=1, ASH) in the RCP4.5 control run and the A2 and A3 experiments.
As mentioned in the introduction, the neglect of non-CO2 greenhouse gases in our injection experiments underestimates the required cumulative CO2 injections and associated trade-offs in each approach. This is due to the fact that non-CO2 greenhouse gases directly affect the Earth's energy balance, resulting in either warming or cooling of the atmosphere. Gases like methane and nitrous oxide warm the Earth, while aerosols such as sulfate cool it (e.g., Myhre et al., 2013). The current net effect is a small positive radiative forcing, which, although controversially debated, is expected to increase as the cooling effect of sulfate aerosols is predicted to decline over the next half of this century (Moss et al., 2010; Hansen et al., 2017; Rao et al., 2017).
This modeling study explores the potential and biogeochemical impacts of three different approaches to control the amount of oceanic CCS as a means to fill the gap between the CO2 emissions and climate impacts of the RCP4.5 scenario and a specific temperature target such as the 1.5 ∘C climate target. We do so from the perspective of using only ocean CCS for this purpose.
The analysis of the A1 simulation (first approach) reveals that because of committed warming and the eventual outgassing of some of the injected CO2, it would not be sufficient to inject the residual RCP4.5 CO2 emissions (964 Gt C in total) once a global mean temperature of 1.5 ∘C is exceeded for the first time (in the year 2045) until the year 3020. In order to overcome the observed overshoot of +0.7 ∘ C by the year 3020 in the first approach, we find that about 600 Gt C (62 %) more needs to be injected, as indicated by the default simulation of the second approach, i.e., the A2 run (Figs. 1a, b and 2b).
Following the atmospheric CO2 concentration of the RCP/ECP2.6 as closely as possible by applying oceanic CCS would require cumulative CO2 injections of about 2200 Gt C until the year 3020. However, global mean temperature reaches +0.9 ∘C by the end of the A3 simulation and thus undershoots the respective climate target.
The cumulative CO2 injections in the second and third approach and the respective required emission reductions question the suitability of oceanic CCS for the aspired target on such a timescale because the outgassed CO2 amounts, which are 607 and 900 Gt C by the year 3020, respectively (Figs. 1d and 2b, c), would need to be recaptured by additional technologies such as direct air capture and subsequently reinjected into the deep ocean. The required emission reductions of about 955 Gt C in the second approach and about 1300 Gt C in the third approach point to the massive CO2 amounts that would need to get removed from the atmosphere under the RCP/ECP4.5 CO2 emission scenario in order to be compatible with the 1.5 ∘C or lower climate target on a millennium timescale.
From the integrated analysis of the model runs from all three approaches (i.e., eye-fitted lines in Fig. 2b and c), we quantify the amount of emission reduction and oceanic CCS, respectively, required to lower the model-predicted global mean temperature by 1 ∘C. In the near future (2100) this measure is 446 Gt C ∘C−1 for both oceanic CCS and the required emission reductions as only a tiny fraction has outgassed until that point in time (see Sect. 3.1). On a millennial timescale this measure is about 951 Gt C ∘C−1 for oceanic CCS and about 595 Gt C ∘C−1 (37 % less) for the required emission reductions, respectively, highlighting that a large fraction of injected CO2 has outgassed.
Inclusion of CaCO3 sediment and weathering feedbacks reduces the required cumulative CO2 injections and required emission reductions by about 6 % in the first and third approach and by about 11 % in the second approach, respectively (Fig. 2b and c). The neglect of non-CO2 greenhouse gases in the applied forcing of the injection experiments underestimates the cumulative CO2 injections that would be required. In general, it is estimated that non-CO2 climate agents contribute between 10 % and 30 % to the total forcing (Friedlingstein et al., 2014) until the year 2100 and for business-as-usual simulations. Extrapolating the current contribution of greenhouse gases other than CO2 qualitatively into the future, we expect that CO2 injections of the magnitude of the A3 simulation may be required to stay safely below +1.5 ∘C on a millennium timescale. We propose that our generalized estimates of emission reduction and oceanic CCS per 1 ∘C cooling, respectively, may be used in the future to quantify additional efforts in order to compensate for non-CO2 greenhouse-gases-induced warming.
With respect to the biogeochemical impacts in the injection simulations of the second and third approach, we observe an increase of the average pH and aragonite saturation states in the surface ocean (0–130 m) after the start of oceanic CCS, when compared to the RCP4.5 control run. These are due to the direct effect of a lower atmospheric pCO2 in the injection experiments, i.e., reduced upper-ocean acidification (Sect. 3.3).
Potential tropical coral reef habitats in the upper-ocean volume, which are here defined as having an ΩAR>3.4 and ocean temperatures between 21 and 28 ∘C, are observed to steadily increase after the start of oceanic CCS in the A2 run and the A3 simulation (Fig. 5a), almost reaching preindustrial levels in the A3 simulation. However, the potential coral reef habitats in the respective injection experiments are close to zero for several decades (Fig. 5a), raising the question of whether coral reefs would be able to recover from globally inhabitable conditions after this period of time. Local application of ocean alkalinization (Feng et al., 2016) may be a technical solution to protect coral reefs during this time period, in particular in regions where coral reefs are essential for shoreline protections.
The observed reduction of ocean acidification in the surface ocean comes at the expense of more strongly acidified water masses in the intermediate and deep ocean, with the strongest reductions in pH levels in the vicinity of the seven injections sites (Fig. 3d and e). Although it is difficult to predict how this would impact marine ecosystems, it is very likely that such conditions would put them under severe stress.
Overall, the trade-off between injection-related damages in the deep ocean and benefits in the upper ocean illustrate the challenge of evaluating the offset of local harm against global benefit, which is very likely the subject of any deliberate CO2 removal method (e.g., Smith et al., 2016; Boysen et al., 2017; Fuss et al., 2018). Leaving aside the massive economic effort associated with ocean CCS of the size needed to reach the 1.5 ∘C climate target (even when starting from a currently optimistic RCP4.5 mitigation scenario), humanity will have to decide whether severe stress and potential loss of deep-sea ecosystems is acceptable when paid off by conserving or restoring surface ocean ecosystems to a large extent.
The model data used to generate the table and figures are available online at https://data.geomar.de/thredds/catalog/open_access/reith_et_al_2019_esd/catalog.html (Reith et al., 2019).
The supplement related to this article is available online at: https://doi.org/10.5194/esd-10-711-2019-supplement.
All authors conceived and designed the experiments. FR implemented the experiments with contributions from WK and JG. FR performed the experiments and analyzed the data. FR wrote the paper with contributions from all co-authors.
The authors declare that they have no conflict of interest.
The Deutsche Forschungsgemeinschaft (DFG) financially supported this study via the Priority Programme 1689.
This research has been supported by the Deutsche Forschungsgemeinschaft (grant no. SPP1689).
The article processing charges for this open-access publication were covered by the Biogeochemical Modelling research unit of GEOMAR, a Research Centre of the Helmholtz Association.
This paper was edited by Govindasamy Bala and reviewed by two anonymous referees.
Allen, M. R., Frame, D. J., Huntingford, C., Jones, C. D., Lowe, J. A., Meinshausen, M., and Meinshausen, N.: Warming caused by cumulative carbon emissions towards the trillionth tonne, Nature, 458, 1163–1166, https://doi.org/10.1038/nature08019, 2009.
Archer, D.: A data-driven model of the global calcite lysocline, Global Biogeochem. Cy., 10, 511–526, https://doi.org/10.1029/96GB01521, 1996.
Archer, D.: Fate of fossil fuel CO2 in geologic time, J. Geophys. Res.-Oceans, 110, 1–6, https://doi.org/10.1029/2004JC002625, 2005.
Archer, D., Kheshgi, H. S., and Maier-Reimer, E.: Dynamics of fossil fuel CO2 neutralization by marine CaCO3, Glob. Biogeochem. Cy., 12, 259–276, 1998.
Bigalke, N. K., Rehder, G., and Gust, G.: Experimental investigation of the rising behavior of CO2 droplets in seawater under hydrate-forming conditions, Environ. Sci. Technol., 42, 5241–5246, https://doi.org/10.1021/es800228j, 2008.
Bitz, C. M. and Lipscomb, W. H.: An energy-conserving thermodynamic model of sea ice, J. Geophys. Res., 104, 15669, https://doi.org/10.1029/1999JC900100, 1999.
Boysen, L., Lucht, W., Schellnhuber, H., Gerten, D., Heck, V., and Lenton, T.: The limits to global-warming mitigation by terrestrial carbon removal, Earth's Future, 5, 1–12, https://doi.org/10.1002/2016EF000469, 2017.
Cao, L., Eby, M., Ridgwell, A., Caldeira, K., Archer, D., Ishida, A., Joos, F., Matsumoto, K., Mikolajewicz, U., Mouchet, A., Orr, J. C., Plattner, G.-K., Schlitzer, R., Tokos, K., Totterdell, I., Tschumi, T., Yamanaka, Y., and Yool, A.: The role of ocean transport in the uptake of anthropogenic CO2, Biogeosciences, 6, 375–390, https://doi.org/10.5194/bg-6-375-2009, 2009.
Ciais, P., Sabine, C., Bala, G., Bopp, L., Brovkin, V., Canadell, J., Chhabra, A., DeFries, R., Galloway, J., Heimann, M., Jones, C., Le Quéré, C., Myneni, R. B., Piao, S., and Thornton, P.: Carbon and Other Biogeochemical Cycles, in: Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, UK and New York, NY, USA, 2013.
Clarke, L. E., Jiang, K., Akimoto, K., Babiker, M., Blanford, G., Fisher-Vanden, K., Hourcade, J.-C., Krey, V., Kriegler, E., Löschel, A., McCollum, D., Paltsev, S., Rose, S., Shukla, P. R., Tavoni, M., van der Zwaan, B. C. C., and van Vuuren, D. P.: Assessing transformation pathways, in: Clim. Chang. 2014 Mitig. Clim. Chang. Contrib. Work. Gr. III to Fifth Assess. Rep. Intergov. Panel Clim. Chang., Earth's Future, 5, 463–474, 2014.
Clémençon, R.: The Two Sides of the Paris Climate Agreement, J. Environ. Dev., 25, 3–24, https://doi.org/10.1177/1070496516631362, 2016.
Collins, M., Knutti, R., Arblaster, J., Dufresne, J.-L., Fichefet, T., Friedlingstein, P., Gao, X., Gutowski, W. J., Johns, T., Krinner, G., Shongwe, M., Tebaldi, C., Weaver, A. J., and Wehner, M.: Long-term Climate Change: Projections, Commitments and Irreversibility, in: Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, UK and New York, NY, USA, 2013.
DeVries, T. and Primeau, F.: Dynamically and Observationally Constrained Estimates of Water-Mass Distributions and Ages in the Global Ocean, J. Phys. Oceanogr., 41, 2381–2401, https://doi.org/10.1175/JPO-D-10-05011.1, 2011.
Dickson, A. G. and Millero, F. J.: A comparison of the equilibrium constants for the dissociation of carbonic acid in seawater media, Deep-Sea Res. Pt. A, 34, 1733–1743, https://doi.org/10.1016/0198-0149(87)90021-5, 1987.
Doney, S. C., Fabry, V. J., Feely, R. A., and Kleypas, J. A.: Ocean acidification: the other CO2 problem, Ann. Rev. Mar. Sci., 1, 169–192, https://doi.org/10.1146/annurev.marine.010908.163834, 2009.
Eby, M., Zickfeld, K., Montenegro, A.., Archer, D., Meissner, K. J., and Weaver, A. J.: Lifetime of anthropogenic climate change: Millennial time scales of potential CO2 and surface temperature perturbations, J. Climate, 22, 2501–2511, https://doi.org/10.1175/2008JCLI2554.1, 2009.
Fabricius, K. E., Kluibenschedl, A., Harrington, L., Noonan, S., and De'ath, G.: In situ changes of tropical crustose coralline algae along carbon dioxide gradients, Sci. Rep., 5, 9537, https://doi.org/10.1038/srep09537, 2015.
Fanning, A. F. and Weaver, A. J.: An atmospheric energy-moisture balance model: Climatology, interpentadal climate change, and coupling to an ocean general circulation model, J. Geophys. Res., 101, 15111, https://doi.org/10.1029/96JD01017, 1996.
Feng, E. Y., Keller, D. P., Koeve, W., and Oschlies, A.: Could artificial ocean alkalinization protect tropical coral ecosystems from ocean acidification?, Environ. Res. Lett., 11, 74008, https://doi.org/10.1088/1748-9326/11/7/074008, 2016.
Flögel, S., Dullo, W. C., Pfannkuche, O., Kiriakoulakis, K., and Rüggeberg, A.: Geochemical and physical constraints for the occurrence of living cold-water corals, Deep-Sea Res. Pt. II, 99, 19–26, https://doi.org/10.1016/j.dsr2.2013.06.006, 2014.
Friedlingstein, P., Andrew, R. M., Rogelj, J., Peters, G. P., Canadell, J. G., Knutti, R., Luderer, G., Raupach, M. R., Schaeffer, M., Van Vuuren, D. P., and Le Quéré, C.: Persistent growth of CO2 emissions and implications for reaching climate targets, Nat. Publ. Gr., 7, 709–715, https://doi.org/10.1038/ngeo2248, 2014.
Fuss, S., Canadell, J. G., Peters, G. P., Tavoni, M., Andrew, R. M., Ciais, P., Jackson, R. B., Jones, C. D., Kraxner, F., Nakicenovic, N., Le Quéré, C., Raupach, M. R., Sharifi, A., Smith, P., and Yamagata, Y.: Betting on negative emissions, Nat. Clim. Change, 4, 850–853, https://doi.org/10.1038/nclimate2392, 2014.
Fuss, S., Lamb, W. F., Callaghan, M. W., Hilaire, J., Creutzig, F., Amann, T., Beringer, T., De Oliveira Garcia, W., Hartmann, J., Khanna, T., Luderer, G., Nemet, G. F., Rogelj, J., Smith, P., Vicente, J. V., Wilcox, J., Del Mar Zamora Dominguez, M., and Minx, J. C.: Negative emissions – Part 2: Costs, potentials and side effects, Environ. Res. Lett., 13, 063002, https://doi.org/10.1088/1748-9326/aabf9f, 2018.
Gasser, T., Guivarch, C., Tachiiri, K., Jones, C. D., and Ciais, P.: Negative emissions physically needed to keep global warming below 2 ∘C, Nat. Commun., 6, 7958, https://doi.org/10.1038/ncomms8958, 2015.
Gehlen, M., Séférian, R., Jones, D. O. B., Roy, T., Roth, R., Barry, J., Bopp, L., Doney, S. C., Dunne, J. P., Heinze, C., Joos, F., Orr, J. C., Resplandy, L., Segschneider, J., and Tjiputra, J.: Projected pH reductions by 2100 might put deep North Atlantic biodiversity at risk, Biogeosciences, 11, 6955–6967, https://doi.org/10.5194/bg-11-6955-2014, 2014.
Gillett, N. P., Arora, V. K., Zickfeld, K., Marshall, S. J., and Merryfield, W. J.: Ongoing climate change following a complete cessation of carbon dioxide emissions, Nat. Geosci., 4, 83–87, https://doi.org/10.1038/ngeo1047, 2011.
Guinotte, J. M. and Fabry, V. J.: Ocean acidification and its potential effects on marine ecosystems, Ann. N. Y. Acad. Sci., 1134, 320–342, https://doi.org/10.1196/annals.1439.013, 2008.
Hansen, J., Sato, M., Kharecha, P., von Schuckmann, K., Beerling, D. J., Cao, J., Marcott, S., Masson-Delmotte, V., Prather, M. J., Rohling, E. J., Shakun, J., Smith, P., Lacis, A., Russell, G., and Ruedy, R.: Young people's burden: requirement of negative CO2 emissions, Earth Syst. Dynam., 8, 577–616, https://doi.org/10.5194/esd-8-577-2017, 2017.
Hoffert, M. I., Wey, Y. C., Callegari, A. J., and Broecker, W. S.: Atmospheric response to deep-sea injections of fossil-fuel carbon dioxide, Climatic Change, 2, 53–68, https://doi.org/10.1007/BF00138226, 1979.
Horton, J. B., Keith, D. W., and Honegger, M.: Implications of the Paris Agreement for Carbon Dioxide Removal and Solar Geoengineering, Policy Brief, Harvard Project on Climate Agreements, Belfer Center, 2016.
IPCC – Intergovernmental Panel on Climate Change: Special Report on Carbon Dioxide Capture and Storage, edited by: Metz, B., Davidson, O., de Coninck, H. C., Loos, M., and Meyer, L. A., Cambridge University Press, Cambridge, UK and New York, NY, USA, 422 pp., 2005.
IPCC – Intergovernmental Panel on Climate Change: Workshop Report of the IPCC Workshop on Impacts of Ocean Acidification on Marine Biology and Ecosystems, edited by: Field, C. B., Barros, V., Stocker, T. F., Qin, D., Mach, K. J., Plattner, G.-K., Mastrandrea, M. D., Tignor, M., and Ebi, K. L., IPCC Working Group II Technical Support Unit, Carnegie Institution, Stanford, California, USA, 164 pp., 2011.
IPCC – Intergovernmental Panel on Climate Change: Climate change 2014: impacts, adaptation, and vulnerability. Part A: Global and Sectoral Aspects, in: Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Field, C. B., Barros, V. R., and Dokken, D. J., Cambridge University Press, Cambridge, UK and New York, NY, USA, 2014.
Jain, A. K. and Cao, L.: Assessing the effectiveness of direct injection for ocean carbon sequestration under the influence of climate change, Geophys. Res. Lett., 32, L09609, https://doi.org/10.1029/2005GL022818, 2005.
Keeling, R. F.: Triage in the greenhouse, Nat. Geosci., 2, 820–822, https://doi.org/10.1038/ngeo701, 2009.
Keller, D. P., Oschlies, A., and Eby, M.: A new marine ecosystem model for the University of Victoria Earth System Climate Model, Geosci. Model Dev., 5, 1195–1220, https://doi.org/10.5194/gmd-5-1195-2012, 2012.
Keller, D. P., Feng, E. Y., and Oschlies, A.: Potential climate engineering effectiveness and side effects during a high carbon dioxide-emission scenario, Nat. Commun., 5, 3304, https://doi.org/10.1038/ncomms4304, 2014.
Keller, D. P., Lenton, A., Littleton, E. W., Oschlies, A., Scott, V., and Vaughan, N. E.: The Effects of Carbon Dioxide Removal on the Carbon Cycle, Curr. Clim. Change Rep., 4, 250–265, https://doi.org/10.1007/s40641-018-0104-3, 2018.
Kleypas, J. A., McManus, J. W., and Menez, L.: Environmental limits to coral reef development: Where do we draw the line?, Am. Zool., 39, 146–159, 1999.
Knopf, B., Fuss, S., Hansen, G., Creutzig, F., Minx, J., and Edenhofer, O.: From Targets to Action: Rolling up our Sleeves after Paris, Glob. Challeng., 1, 1600007, https://doi.org/10.1002/gch2.201600007, 2017.
Knutti, R., Rogelj, J., Sedláček, J., and Fischer, E. M.: A scientific critique of the two-degree climate change target, Nat. Geosci., 9, 13–18, https://doi.org/10.1038/ngeo2595, 2015.
Koeve, W. and Oschlies, A.: Potential impact of DOM accumulation on fCO2 and carbonate ion computations in ocean acidification experiments, Biogeosciences, 9, 3787–3798, https://doi.org/10.5194/bg-9-3787-2012, 2012.
Le Quéré, C., Andrew, R. M., Canadell, J. G., Sitch, S., Ivar Korsbakken, J., Peters, G. P., Manning, A. C., Boden, T. A., Tans, P. P., Houghton, R. A., Keeling, R. F., Alin, S., Andrews, O. D., Anthoni, P., Barbero, L., Bopp, L., Chevallier, F., Chini, L. P., Ciais, P., Currie, K., Delire, C., Doney, S. C., Friedlingstein, P., Gkritzalis, T., Harris, I., Hauck, J., Haverd, V., Hoppema, M., Klein Goldewijk, K., Jain, A. K., Kato, E., Körtzinger, N., Lenton, A., Lienert, S., Lombardozzi, D., Melton, J. R., Metzl, N., Millero, F., Monteiro, P. M. S., Munro, D. R., Nabel, J. E. M. S., Nakaoka, S. I., O'Brien, K., Olsen, A., Omar, A. M., Ono, T., Pierrot, D., Poulter, Salisbury, J., Schuster, U., Schwinger, J., R., Skjelvan, I., Stocker, B. D., Sutton, A. J., Takahashi, T., Tian, H., Tilbrook, B., Van Der Laan-Luijkx, I. T., Van Der Werf, G. R., Viovy, N., Walker, A. P., Wiltshire, A. J., and Zaehle, S.: Global Carbon Budget 2016, Earth Syst. Sci. Data, 8, 605–649, https://doi.org/10.5194/essd-8-605-2016, 2016.
Leung, D. Y. C., Caramanna, G., and Maroto-Valer, M. M.: An overview of current status of carbon dioxide capture and storage technologies, Renew. Sustain. Energy Rev., 39, 426–443, https://doi.org/10.1016/j.rser.2014.07.093, 2014.
Lewis, E. and Wallace, D. W. R.: Program developed for CO2 system calculations, Carbon Dioxide Information Analysis Center, Report ORNL/CDIAC-105, Oak Ridge National Laboratory, Oak Ridge, Tennessee, USA, 1998.
Lischka, S., Büdenbender, J., Boxhammer, T., and Riebesell, U.: Impact of ocean acidification and elevated temperatures on early juveniles of the polar shelled pteropod Limacina helicina: Mortality, shell degradation, and shell growth, Biogeosciences, 8, 919–932, https://doi.org/10.5194/bg-8-919-2011, 2011.
MacDougall, A. H.: The Transient Response to Cumulative CO2 Emissions: a Review, Curr. Clim. Change Rep., 2, 39–47, https://doi.org/10.1007/s40641-015-0030-6, 2016.
Marchetti, C.: On geoengineering and the CO2 problem, Climatic Change, 1, 59–68, https://doi.org/10.1007/BF00162777, 1977.
Matthews, H. D. and Caldeira, K.: Stabilizing climate requires near-zero emissions, Geophys. Res. Lett., 35, 1–5, https://doi.org/10.1029/2007GL032388, 2008.
Matthews, H. D., Gillett, N. P., Stott, P. A., and Zickfeld, K.: The proportionality of global warming to cumulative carbon emissions, Nature, 459, 829–832, https://doi.org/10.1038/nature08047, 2009.
Mehrbach, C., Culberson, C. H., Hawley, J. E., and Pytkowicx, R. M.: Measurement of the Apparent Dissociation Constants of Carbonic Acid in Seawater At Atmospheric Pressure1, Limnol. Oceanogr., 18, 897–907, https://doi.org/10.4319/lo.1973.18.6.0897, 1973.
Meinshausen, M., Smith, S. J., Calvin, K., Daniel, J. S., Kainuma, M. L. T., Lamarque, J., Matsumoto, K., Montzka, S. a., Raper, S. C. B., Riahi, K., Thomson, A., Velders, G. J. M., and van Vuuren, D. P. P.: The RCP greenhouse gas concentrations and their extensions from 1765 to 2300, Climatic Change, 109, 213–241, https://doi.org/10.1007/s10584-011-0156-z, 2011.
Meissner, K. J., Weaver, A. J., Matthews, H. D., and Cox, P. M.: The role of land surface dynamics in glacial inception: A study with the UVic Earth System Model, Clim. Dynam., 21, 515–537, https://doi.org/10.1007/s00382-003-0352-2, 2003.
Mengis, N., Partanen, A. I., Jalbert, J., and Matthews, H. D.: 1.5 ∘C carbon budget dependent on carbon cycle uncertainty and future non-CO2 forcing, Sci. Rep., 8, 1–7, https://doi.org/10.1038/s41598-018-24241-1, 2018.
Millero, F. J.: Thermodynamics of the carbon dioxide system in the ocean, Geochim. Cosmochim. Ac., 59, 661–677, 1995.
Moss, R. H., Edmonds, J. A., Hibbard, K. A., Manning, M. R., Rose, S. K., van Vuuren, D. P., Carter, T. R., Emori, S., Kainuma, M., Kram, T., Meehl, G. A., Mitchell, J. F. B., Nakicenovic, N., Riahi, K., Smith, S. J., Stouffer, R. J., Thomson, A. M., Weyant, J. P., and Wilbanks, T. J.: The next generation of scenarios for climate change research and assessment, Nature, 463, 747–756, https://doi.org/10.1038/nature08823, 2010.
Mucci A.: The solubility of calcite and aragonite in seawater at various salinities, temperatures and one atmosphere total pressure, Am. J. Sci., 283, 780–799, 1983.
Myhre, G., Samset, B. H., Schulz, M., Balkanski, Y., Bauer, S., Berntsen, T. K., Bian, H., Bellouin, N., Chin, M., Diehl, T., Easter, R. C., Feichter, J., Ghan, S. J., Hauglustaine, D., Iversen, T., Kinne, S., Kirkeväg, A., Lamarque, J. F., Lin, G., Liu, X., Lund, M. T., Luo, G., Ma, X., Van Noije, T., Penner, J. E., Rasch, P. J., Ruiz, A., Seland, Skeie, R. B., Stier, P., Takemura, T., Tsigaridis, K., Wang, P., Wang, Z., Xu, L., Yu, H., Yu, F., Yoon, J. H., Zhang, K., Zhang, H., and Zhou, C.: Radiative forcing of the direct aerosol effect from AeroCom Phase II simulations, Atmos. Chem. Phys., 13, 1853–1877, https://doi.org/10.5194/acp-13-1853-2013, 2013.
Ogden, L. E.: Marine Life on Acid, Bioscience, 63, 322–328, https://doi.org/10.1525/bio.2013.63.5.3, 2013.
Orr, J. C.: Modelling of ocean storage of CO2 – The GOSAC study, Report PH4/37, in: IEA Greenhouse gas R&D Programme, 96 pp., available at: https://www.lsce.ipsl.fr/Phocea/Pisp/index.php?nom=james.orr (last access: November 2019), 2004.
Orr, J. C., Najjar, C. R., Sabine, C. L., and Joos, F.: Abiotic-Howto, Internal OCMIP Report, LCSE/CEA Saclay, Gif-sur-Yvette, France, 25 pp., 1999.
Orr, J. C., Aumont, O., Yool, A., Plattner, K., Joos, F., Maier-Reimer, E., Weirig, M.-F., Schlitzer, R., Caldeira, K., Wicket, M., and Matear, R.: Ocean CO2 Sequestration Efficiency from 3-D Ocean Model Comparison, in: Greenhouse Gas Control Technologies, edited by: Williams, D., Durie, B., McMullan, P., Paulson, C., and Smith, A., CSIRO, Colligwood, Australia, 469–474, 2001.
Pacanowski, R. C.: MOM2, Documentation, User's Guide and Reference Manual, GFDL Ocean Technical Report 3.2, Geophysical Fluid Dynamics Laboratory/NOAA, Princeton, 329 pp., 2016.
Pandolfi, J. M., Connolly, S. R., Marshall, D. J., and Cohen, A. L.: Projecting Coral Reef Futures Under Global Warming and Ocean Acidification, Science, 333, 418–422, https://doi.org/10.1126/science.1204794, 2011.
Rao, S., Klimont, Z., Smith, S. J., Van Dingenen, R., Dentener, F.,Bouwman, L., Riahi, K., Amann, M., Bodirsky, B. L., van Vuuren, D. P., Reis, L. A., Calvin, K., Drouet, L., Fricko, O., Fujimori, S., Gernaat, D., Havlik, P., Harmsen, M., Hasegawa, T., Heyes, C., Hilaire, J., Luderer, G., Masui, T., Stehfest, E., Strefler, J., van der Sluis, S., and Tavoni, M.: Future air pollution in the Shared Socio-economic Pathways, Global Environ. Change, 42, 346–358, 2017.
Reith, F., Keller, D. P., and Oschlies, A.: Revisiting ocean carbon sequestration by direct injection: A global carbon budget perspective, Earth Syst. Dynam., 7, 797–812, https://doi.org/10.5194/esd-7-797-2016, 2016.
Reith, F., Koeve, W., Keller, D. P., Getzlaff, J., and Oschlies, A.: Model data used to generate the table and figures of this publication, available at: https://data.geomar.de/thredds/catalog/open_access/reith_et_al_2019_esd/catalog.html, 2019
Resplandy, L., Bopp, L., Orr, J. C., and Dunne, J. P.: Role of mode and intermediate waters in future ocean acidification: Analysis of CMIP5 models, Geophys. Res. Lett., 40, 3091–3095, https://doi.org/10.1002/grl.50414, 2013.
Ricke, K. L., Orr, J. C., Schneider, K., and Caldeira, K.: Risks to coral reefs from ocean carbonate chemistry changes in recent earth system model projections, Environ. Res. Lett., 8, 34003, https://doi.org/10.1088/1748-9326/8/3/034003, 2013.
Ridgwell, A., Rodengen, T. J., and Kohfeld, K. E.: Geographical variations in the effectiveness and side effects of deep ocean carbon sequestration, Geophys. Res. Lett., 38, 1–6, https://doi.org/10.1029/2011GL048423, 2011.
Roberts, J. M. and Cairns, S. D.: Cold-water corals in a changing ocean, Curr. Opin. Environ. Sustain., 7, 118–126, https://doi.org/10.1016/j.cosust.2014.01.004, 2014.
Rockström, J., Steffen, W., Noone, K., Persson, Å., Chapin III, F. S., Lambin, E. F., Lenton, T. M., Scheffer, M., Folke, C., Schellnhuber, H., Nykvist, B., de Wit, C. A., Hughes, T., van der Leeuw, S., Rodhe, H., Sörlin, S., Snyder, P. K., Costanza, R., and Al, E.: Planetary Boundaries: Exploring the Safe Operating Space for Humanity, Ecol. Soc., 14, 32, https://doi.org/10.1038/461472a, 2009.
Rockström, J., Schellnhuber, H., Hoskins, B., Ramanathan, V., Brasseur, G., Gaffney, O., Nobre, C., Meinshausen, M., and Lucht, W.: Earth's Future The world's biggest gamble Earth's Future, Earth's Future, 4, 465–470, https://doi.org/10.1002/2016EF000392, 2016.
Rogelj, J., Den Elzen, M., Fransen, T., Fekete, H., Winkler, H., Schaeffer, R., Sha, F., Riahi, K., and Meinshausen, M.: Perspective: Paris Agreement climate proposals need boost to keep warming well below 2 ∘C, Nat. Clim. Change, 534, 631–639, https://doi.org/10.1038/nature18307, 2016.
Sabine, C. L., Feely, R. A., Gruber, N., Key, R. M., Lee, K., Bullister, J. L., Wanninkhof, R., Wong, C. S., Wallace, D. W. R., Tilbrook, B., Millero, F. J., Peng, T.-H., Kozyr, A., Ono, T., and Rios, A. F.: The oceanic sink for anthropogenic CO2, Science, 305, 367–371, https://doi.org/10.1126/science.1097403, 2004.
Sanderson, B. M., O'Neill, B. C., and Tebaldi, C.: What would it take to achieve the Paris temperature targets?, Geophys. Res. Lett., 43, 7133–7142, https://doi.org/10.1002/2016GL069563, 2016.
Sarmiento, J. L. and Toggweiler, J. R.: A new model for the role of the oceans in determining atmospheric PCO2, Nature, 308, 621–624, https://doi.org/10.1038/308621a0, 1984.
Schubert, R., Schellnhuber, H. J., Buchmann, N., Epiney, A., Griesshammer, R., Kulessa, M., Messner, D., Rahmstorf, S., and Schmid, J.: The Future Oceans – Warming Up, Rising High, Turning Sour., Wissenchaftlicher Beirat der Bundesregierung (WBGU), Berlin, 2006.
Smith, P., Davis, S. J., Creutzig, F., Fuss, S., Minx, J., Gabrielle, B., Kato, E., Jackson, R. B., Cowie, A., Kriegler, E., van Vuuren, D. P., Rogelj, J., Ciais, P., Milne, J., Canadell, J. G., McCollum, D., Peters, G., Andrew, R., Krey, V., Shrestha, G., Friedlingstein, P., Gasser, T., Grubler, A., Heidug, W. K., Jonas, M., Jones, C. D., Kraxner, F., Littleton, E., Lowe, J., Moreira, J. R., Nakicenovic, N., Obersteiner, M., Patwardhan, A., Rogner, M., Rubin, E., Sharifi, A., Torvanger, A., Yamagata, Y., Edmonds, J., and Yongsung, C.: Biophysical and economic limits to negative CO2 emissions, Nat. Clim. Change, 6, 42–50, https://doi.org/10.1038/nclimate2870, 2016.
UNFCCC: Conference of the Parties: Adoption of the Paris Agreement, Proposal by the President, Paris Clim. Chang. Conf. – Novemb. 2015, COP 21, 21932 (December 2015), 31, available at: http://unfccc.int/resource/docs/2015/cop21/eng/l09.pdf (last access: 14 April 2018), 2015.
van Heuven, S., Pierrot, D., Lewis, E., and Wallace, D. W. R.: MATLAB Program Developed for CO2 System Calculations, ORNL/CDIAC-105b, Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, US Department of Energy, Oak Ridge, Tennessee, available at: ftp://cdiac.ornl.gov/pub/co2sys/CO2SYScalcMATLAB (last access: 14 April 2018), 2009.
Volk, T. and Hoffert, M. I.: Ocean carbon pumps: Analysis of relative strengths and efficiencies in ocean driven atmospheric CO2 changes, in: The Carbon Cycle and Atmospheric CO2: Natural variations Archaean to present, edited by: Sundquist, E. T. and Broecker, W. S., Geophys. Monogr. Ser., AGU, Washington, D.C., 32, 99–110, 1985.
Weaver, A. J., Eby, M., Wiebe, E. C., Bitz, C. M., Duffy, P. B., Ewen, T. L., Fanning, A. F., Holland, M. M., MacFadyen, A., Matthews, H. D., Meissner, K. J., Saenko, O., Schmittner, A., Wang, H., and Yoshimori, M.: The UVic earth system climate model: Model description, climatology, and applications to past, present and future climates, Atmos.-Ocean, 39, 361–428, https://doi.org/10.1080/07055900.2001.9649686, 2001.
Williamson, P.: Emissions reduction: Scrutinize CO2 removal methods, Nature, 530, 5–7, https://doi.org/10.1038/530153a, 2016.
Zeebe, R. E.: History of Seawater Carbonate Chemistry, Atmospheric CO2, and Ocean Acidification, Annu. Rev. Earth Planet. Sci., 40, 141–165, https://doi.org/10.1146/annurev-earth-042711-105521, 2012.
Zickfeld, K. and Herrington, T.: The time lag between a carbon dioxide emission and maximum warming increases with the size of the emission, Environ. Res. Lett., 10, 31001, https://doi.org/10.1088/1748-9326/10/3/031001, 2015.
Zickfeld, K., MacDougall, A. H., and Matthews, H. D.: On the proportionality between global temperature change and cumulative CO2 emissions during periods of net negative CO2 emissions, Environ. Res. Lett., 11, 55006, https://doi.org/10.1088/1748-9326/11/5/055006, 2016.





