the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Complementing CO2 emission reduction by solar radiation management might strongly enhance future welfare
Koen G. Helwegen
Claudia E. Wieners
Jason E. Frank
Henk A. Dijkstra
Solar radiation management (SRM) has been proposed as a means to reduce global warming in spite of high greenhouse-gas concentrations and to lower the chance of warming-induced tipping points. However, SRM may cause economic damages and its feasibility is still uncertain. To investigate the trade-off between these (economic) gains and damages, we incorporate SRM into a stochastic dynamic integrated assessment model and perform the first rigorous cost–benefit analysis of sulfate-based SRM under uncertainty, treating warming-induced climate tipping and SRM failure as stochastic elements. We find that within our model, SRM has the potential to greatly enhance future welfare and merits being taken seriously as a policy option. However, if only SRM and no CO2 abatement is used, global warming is not stabilised and will exceed 2 K. Therefore, even if successful, SRM can not replace but only complement CO2 abatement. The optimal policy combines CO2 abatement and modest SRM and succeeds in keeping global warming below 2 K.
Despite the Paris Agreement target to keep global mean temperature change “well below 2 K” in order to prevent “dangerous climate change” (UNFCCC, 2015), no decisive reduction of CO2 emissions has yet taken place (Le Quéré et al., 2018). This has sparked renewed interest in the possibility of cooling the climate system by geoengineering (Crutzen, 2006). Among several suggested approaches, only solar radiation management (SRM), i.e. reflecting part of the incoming solar radiation back into space, has the potential to offset the global mean temperature changes projected by 2100 (Keller et al., 2014).
Several SRM techniques have been proposed (Latham et al., 2008; Ahlm et al., 2017; Gabriel et al., 2017; Seneviratne et al., 2018), although for some of them it is yet unknown whether they will be effective in cooling the planet and whether they will be technically feasible. The scheme that is most likely to become ripe for employment in the near future is sulfate-aerosol-based SRM (McClellan et al., 2010; Moriyama et al., 2017). The scheme involves injecting precursor gases such as SO2 into the stratosphere. This leads to the formation of reflective sulfate aerosols in the lower stratosphere which increases the Earth's albedo and causes surface cooling. Such cooling – of about 0.4 K over several years (Stowe et al., 1990; Thompson et al., 2009) – was observed following the Pinatubo eruption (Stowe et al., 1990; Thompson et al., 2009; Stenchikov et al., 1998; Robock, 2000), which injected 8–10 Mt(S) (megatonnes of sulfur), mainly as SO2, into the stratosphere (Ward, 2009). It is still uncertain whether SRM can completely eliminate future global warming. High aerosol concentrations lead to faster coagulation, which reduces albedo and accelerates deposition (Visioni et al., 2017). One study (Kleinschmitt et al., 2018) suggests that SRM cannot provide a stronger negative radiative forcing than −2 W m−2, while others find that sufficiently strong forcing can be achieved, albeit at very high injection rates (Niemeyer and Timmreck, 2015; Niemeyer and Schmidt, 2017).
The potential benefits of SRM are obvious: a reduction of global warming and warming-induced damages and a reduced transition likelihood of temperature-related climate tipping points (Cai et al., 2016). However, SRM cannot avert all climate change (Kravitz et al., 2013). In particular, global mean precipitation is expected to decrease (Andrews et al., 2010; MacMartin and Kravitz, 2016), and the spatial precipitation patterns may change. Ocean acidification will continue unless atmospheric CO2 concentrations are reduced (Tjiputra et al., 2015).
The implementation costs of sulfate SRM are estimated to be USD 2–10 billion per megatonne of injected gas (McClellan et al., 2010; Moriyama et al., 2017), which is modest compared to the world GDP of USD 80 trillion (data for 2017; World Bank, 2017). For comparison, building and installing enough solar cells to meet global energy demand would, at current prices, cost about USD 250 trillion, although prices are decreasing rapidly (Cassedy and Grossman, 2017). However, apart from moral issues (Robock et al., 2009), sulfate SRM may have damaging effects on human health (Effiong and Neitzel, 2016) and the environment (Pitari et al., 2014; Ward, 2009) that are still poorly understood (Irvine et al., 2017). A sudden discontinuation of SRM will cause rapid warming (“termination shock”) to levels dictated by greenhouse-gas concentrations (Brovkin et al., 2009; Matthews and Caldeira, 2007), which could put more stress on ecosystems and societies than a gradual warming (Trisos et al., 2018).
At least two major uncertainties are of great importance for cost–benefit analysis of SRM: the possibility of warming-induced tipping behaviour (whose likelihood is reduced by SRM) and the possibility of SRM failure, either by inefficiency (Kleinschmitt et al., 2018) or because (unforseen) damaging side effects force one to abandon it (Robock et al., 2009). In this study we use a stochastic version of the integrated assessment model DICE (Nordhaus, 1992) to compute the (economically) optimal policy including CO2 abatement and SRM.
Here we build on earlier studies, which often included uncertainty only through parameter sensitivity analysis (Goes et al., 2011; Bahn et al., 2015) or as a simplified two-step decision problem (Moreno-Cruz and Keith, 2013). Two recent studies (Heutel et al., 2016, 2018) include climate tipping behaviour and parameter uncertainty in DICE but employ a simple four-step look-ahead scheme that is unsuitable for long-term optimisation. We employ dynamic programming (Bellman, 1957) to perform the first rigorous cost–benefit analysis of SRM under uncertainty, albeit with a simple model.
The DICE model has been criticised for being overly simple (Pindyck, 2017). In particular, it employs a very aggregated damage function for assessing the material and immaterial cost of climate change (see Nordhaus and Boyer, 2000, for the calibration), which ignores irreversibility of damages and delayed damage (e.g. slow melt of ice caps) and which in later model versions (Nordhaus, 2018) has only received minor updates (Auffhammer, 2018) despite new studies on the subject (IPCC, 2014). Neither does it include climate adaptation. In addition, DICE has an overly simplified energy sector with exogenous costs for CO2 reduction and does not include negative emission techniques. Finally, assuming only one global “social planner”, it disregards the possibility of conflict or imperfect collaboration. Despite these shortcomings, we believe DICE to be a useful test bed for exploratory studies, which should serve as a first orientation and be expanded using more detailed models.
The paper is organised as follows: in Sect. 2.1 we present our model GeoDICE, a stochastic DICE model including geoengineering; in Sect. 2.3 we describe the scenarios employed. The results are presented in Sect. 3.1 (deterministic cases) and Sect. 3.2–3.3 (stochastic cases) with a sensitivity analysis in Sect. 3.5. A summary and discussion is presented in Sect. 4.
2.1 GeoDICE: a stochastic DICE model including geoengineering
Our code is based on Cai et al. (2016), which in turn combines the 2013 version of DICE (Nordhaus, 1992, 2018) and the DSICE framework (Cai et al., 2012) for stochastic treatment of DICE. Here, we include SRM as an additional policy option (together with CO2 abatement). To this end, we incorporate the cooling effect, implementation costs, and environmental damages of SRM into DSICE. A summary of the model parameters and their standard values is given in Table 1.
Nordhaus (1992)Table 1Model parameters of the GeoDICE model related to the representation of SRM. The carbon model parameters can be found in Table 5 of Joos et al. (2013), and others in DICE or DSICE (Cai et al., 2012).
2.1.1 SRM and radiative forcing
To the radiative forcing equation, we add a contribution that depends sublinearly on the sulfur injection rate (Niemeyer and Timmreck, 2015). The total radiative forcing F takes the form
The first term FC describes the contribution of the increase C in atmospheric CO2 concentration above the pre-industrial value CPI and is the same as in DICE. The second term Fother represents the effects of other greenhouse gases (e.g. CH4, N2O, halogen compounds) and industrial aerosol. In DICE, this term is prescribed. However, it seems unlikely that a society that makes great efforts towards abating CO2 emissions does nothing towards combatting other pollutants.
Ciais et al. (2013) quantify various forcing agents, some of which we believe can be more easily abated than others. In particular, we assume that roughly 30 % of the current CH4 emissions (contributions related to fossil fuel production, e.g. leakage and biomass burning), 10 % of the N2O emissions (likewise from industry and fossil fuel production), and 100 % of the emission of halogen compounds could be abated, whereas 70 % of the CH4 emissions (natural sources and agriculture) and 90 % of N2O emissions (agriculture) cannot be abated. Tropospheric ozone, another important greenhouse gas, is formed in chemical reactions with pollutants which likewise can be partially abated. As a rough estimate, about 50 % of the radiative forcing stemming from non-CO2 greenhouse gases could be abated. For simplicity, we assume that this also holds for (mainly cooling) industrial aerosol. Thus we put
where κ=0.5; μ is the abatement of CO2, i.e. the fraction of CO2 emissions avoided; and Fother,DICE is the prescribed contribution used in DICE.
The third term FS describes the influence of sulfate SRM. The sulfate injection leads to a (negative) radiative forcing at the top of the atmosphere which is given by , as found in an atmospheric chemistry modelling study (Niemeyer and Timmreck, 2015), where IS is the annual injection rate of sulfur into the stratosphere (measured in Mt(S) yr−1). To achieve a modest radiative forcing of −2 W m−2 at the top of the atmosphere (TOA), an annual injection of 10 Mt(S) (megatonnes of sulfur), equivalent to one Pinatubo eruption, is required, whereas to achieve a forcing of −8.5 W m−2 (offsetting the greenhouse-gas forcing projected for 2100 under the RCP8.5 scenario), 100 Mt(S) yr−1 is needed. However, due to fast adjustment processes, the TOA radiative forcing is not sufficient to predict the impact on global mean surface temperature (Kravitz et al., 2015). For example, it is found (MacMartin and Kravitz, 2016) that to compensate 7.42 W m−2 forcing from quadrupling CO2, the solar constant would have to be reduced by (4.2±0.6) %, which amounts to 10.1 W m−2 at TOA (taking into account the Earth's albedo). In other words, the top of atmosphere radiative forcing arising from changes in the solar constant is less efficient than forcing caused by CO2 by a factor of We assume here that sulfate SRM has the same efficiency factor η as solar dimming, since both processes take place above the troposphere, and multiply the sulfate SRM contribution to F by this factor in Eq. (1). Note that there is still considerable uncertainty in the forcing efficiency of SRM. For example, Tilmes et al. (2018) find higher efficiencies and an almost linear relationship for injection rates up to 25 Mt(S) yr−1, while Kleinschmitt et al. (2018) suggest that the maximal radiative forcing achievable with sulfate SRM might be limited to 2 W m−2. This possibility that SRM is much less efficient is qualitatively included in the “realistic storyline” scenario described below, which captures that SRM may never work at all. For numerical reasons, we impose an upper bound of IS≤100 Mt(S) yr−1 on the injection rates, i.e. we do not allow them to exceed ≈10 Pinatubo eruptions per year. This upper limit is a much higher injection rate than considered in most detailed studies of the environmental and climate effects of SRM. The limit is never reached except in the somewhat extreme SRM-only scenario (see Sect. 2.3).
2.1.2 Carbon cycle and climate response
We replace the carbon-climate part of DSICE by an emulator of full-fledged climate model simulations (Aengenheyster et al., 2018; MacMartin and Kravitz, 2016). We also include global mean precipitation as a proxy for the residual climate change (changes remaining if SRM is employed to keep global mean temperature constant).
As in DICE, CO2 can be emitted by fossil fuel combustion and land use change. The former contribution is calculated within our model and the latter is prescribed externally using the same values as DICE. We model carbon concentrations based on the Green's function found by Joos et al. (2013).
Current CO2 concentrations C(t) (above pre-industrial levels) can be computed from emissions E at all previous times :
where is the Green's function determining how a unit emission pulse contributes to the concentrations years later, and E(t′) an emission pulse at time t′. Following Joos et al. (2013), GC(s) can be represented as a sum of exponentials, with N=3, and the temporal evolution of C can be rewritten as
Here a0 represents the fraction of carbon emissions staying permanently in the atmosphere. The model parameters an and τn were obtained from a multi-model study (Joos et al., 2013, see their Table 5) and thus represent a best estimate for the behaviour of the carbon cycle, provided that non-linear effects (e.g. saturation of carbon sinks with increasing CO2 concentrations) are small. The initial values are C0=39.01, C1=35.84, C2=21.74, and C3=4.14 ppmv, since our model does not start at pre-industrial times (1765) but in 2005.
For the global mean temperature change (relative to pre-industrial temperature), we follow the same approach, fitting the temperature response to a 1-year pulse of radiative forcing obtained by a multi-model study (MacMartin and Kravitz, 2016) onto a sum of exponentials, obtaining
where F is the radiative forcing from Eq. (1) and other parameters are in Table 1. For the temperature response to a radiative forcing pulse, there is no permanent response T0. The initial values (year 2005) are T1=0.466 and T2=0.436 K.
The response of global mean precipitation P to CO2-induced or SRM-induced radiative forcing is based on MacMartin and Kravitz (2016) and can be split into a slower temperature-driven increase of 2.5 % K−1 and an instantaneous contribution due to CO2 and SRM (Andrews et al., 2010). In particular, increased CO2 concentrations cause additional absorption of longwave radiation, warming the atmosphere and causing a more stable stratification, which suppresses precipitation, while surface warming enhances precipitation. For a gradual increase in CO2 and zero SRM, the temperature-driven effect dominates over the instantaneous contribution, leading to a net moistening. For SRM, the instantaneous contribution is much weaker than for CO2. More specifically, the response of the global mean precipitation P to a 1-year-long 1 W m−2 pulse of radiative forcing from agent f (f stands for CO2 or a change in the solar constant) in year 0, obtained by MacMartin and Kravitz (2016), can be expressed as
where GT is the temperature response to a 1 W m−2 forcing and if t=0 and 0 otherwise. This means that in the year of the forcing pulse, the fast response bf plays a role, whereas in later years the precipitation response is determined by the temperature response. As before, we use the result for reduction in the solar constant as a proxy for sulfate SRM. By lack of data, the fast response to other forcing agents constituting Fother is ignored. With these results, the change in global mean precipitation w.r.t. pre-industrial precipitation levels can be written as
where pTT is the slow precipitation change mediated by warming, whereas pCFC and pSFS are the instantaneous responses expressed in terms of the radiative forcings F. Throughout our study, FC>0 (CO2 leads to a positive radiative forcing) and FS<0 (SRM is used to lower the radiative forcing). As explained above, pT>0 and . Therefore, if SRM were employed such as to cancel the global mean temperature change (, hence T=0), the slow responses stemming from temperature change would cancel and the fast response to CO2 would dominate, reducing P.
We use P as a proxy for residual climate change, i.e. for all effects which remain even if global mean temperature changes are cancelled by SRM.
2.1.3 The damage function and SRM costs
As in DICE (Nordhaus, 1992), the gross domestic product (GDP) is diminished by climate-related damage and by expenditures for climate policy (CO2 abatement and SRM implementation). Including these losses, we retain for the net output
Here, Ω describes damage due to tipping points (see Sect. 2.1.4). If tipping has occurred, then Ω=0.9 (reducing the economic output), otherwise Ω=1 (output not reduced). D≥0 describes non-tipping damage (discussed below). Λ is a factor describing the abatement costs (Λ<1 in case of abatement and Λ=1 in case of no abatement) taken over from DICE-2013 (Nordhaus and Boyer, 2000; Nordhaus, 2018):
where σ(t) is the carbon intensity (amount of carbon released per dollar production, in absence of abatement) and λi are constants. Since CO2 emission is proportional to , so are abatement costs (the more economic output, the more CO2 emissions and hence the higher the costs of eliminating a fraction, μ, of these emissions). λSIS is the implementation cost of SRM, which we assume to be linear in the injection rate IS and independent of . Two studies (McClellan et al., 2010; Moriyama et al., 2017) suggest that the costs for lifting gases to 20 km height are of the order of USD 2–10 billion per megatonne of injected gas. Taking an intermediate value of USD 7 billion per megatonne, and assuming that the gas used is SO2 (which has twice the molecular weight of elementary S), this amounts to USD 14 billion per megatonne of sulfur. Note that H2S would have a lower weight per mole of S, which might reduce transportation costs. However, H2S is also more poisonous and thus potentially difficult to handle. To be conservative, we assumed the costlier solution.
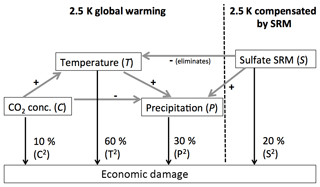
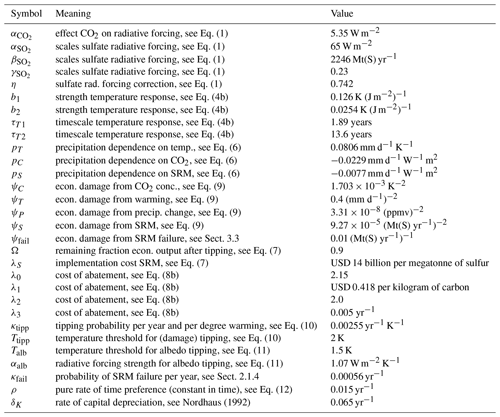
Figure 1Graphical representation of the damage function. The thin black arrows represent contributions to the damage function, while grey arrows depict how the climate variables influence each other (+ and − stand for increasing and decreasing effects, respectively, see Eqs. 4b and 6). The percentages for C, T, and P are based on the contributions of these variables for the standard case of 2.5 K warming in equilibrium and in absence of SRM. In this standard case, our damage equals that of the DSICE model (Cai et al., 2012). The sulfur injections that would be needed to offset 2.5 K warming cause a direct damage of 20 % of the standard damage function.
While the original DICE model assumes that climate-induced damage D scales with the square of temperature change T2 (i.e. D(T)=ψ0T2 with constant ψ0), we keep the quadratic structure but split the damage function into three climate-related contributions and one contribution representing the damage inflicted by sulfate SRM (see Fig. 1):
where T, P, and C are the changes (w.r.t. pre-industrial levels) in global mean temperature, global mean precipitation, and atmospheric CO2 concentration, respectively, and IS the sulfur injection rate in megatonnes of sulfur per year (Mt(S) yr−1). Note that while SRM counteracts the effect of CO2 on both temperature and precipitation, the relative influence of the forcing agents on both variables differs, so that it is not possible to compensate the warming and precipitation change at the same time. Both positive and negative precipitation changes, P, are considered damaging because both require ecosystems and humanity to adapt. An increase in atmospheric CO2 may not be damaging in itself, or may even benefit plant growth (Ciais et al., 2013), but we consider C as a (rough) proxy for ocean acidification, which we do not model explicitly. The coefficients ψ (for values see Table 1) are chosen such that for the standard case of 2.5 K warming in equilibrium without SRM, our total damage equals that of the original DICE model, and the contributions by T, P, and C are 60 %, 30 %, and 10 %, respectively. The standard case was determined by running the climate module of GeoDICE to equilibrium with constant greenhouse-gas concentrations, such as to obtain T=2.5 K. Following Aengenheyster et al. (2018), and approximately in agreement with RCP (representative concentration pathway) scenarios, it was assumed that other forcing agents (other greenhouse gases and aerosols constituting Fother) contribute 14 % to the total radiative forcing. These other forcing agents are not assumed to cause direct damage. The damages associated with the annual sulfur injections needed to offset a warming of 2.5 K are assumed to equal 20 % of the standard case damage.
Previous studies (Heutel et al., 2016, 2018) likewise split the damage function, but without including residual climate change (P). Heutel et al. (2018) assume oceanic and atmospheric CO2 to cause 10 % of the total damage each (20 % in total). However, atmospheric CO2 is not known to cause substantial direct damage and may even be beneficial to plant growth (Ciais et al., 2013), while oceanic CO2 leads to ocean acidification. As mentioned, we do not explicitly compute oceanic CO2 but reduce total CO2-related damage to 10 % because half of the total damage in Heutel et al. (2018) seems in fact small. The splitting between T and P is somewhat arbitrary, but is based on the rough assumption that, although precipitation changes can have a substantial impact, much of the damage is either determined by temperature (especially sea level rise, a major contributor) or at least strongly influenced by it (e.g. hurricanes), hence ψT>ψP. The damage related to SRM depends on the injection rate, not on the percentage of compensated greenhouse-gas forcing as was (somewhat unrealistically) assumed in earlier studies (Heutel et al., 2016, 2018). The choice of ψS is again somewhat arbitrary as virtually no data on the economic damage of SRM is available. However, our main conclusions are unaffected by the exact choice of the parameters ψ (see Sect. 3.5).
2.1.4 Tipping points and SRM failure
Climate change may not only lead to smooth and predictable damages but also induce low-probability, high-impact, and irreversible events such as a collapse of ice sheets (Cai et al., 2015, 2016). The chance of such tipping behaviour is thought to increase with temperature. We take tipping into account in a stylised way, assuming that there is one tipping event that, once activated, reduces GDP by 10 % for all subsequent time steps (i.e. Ω=0.9 in Eq. 7). The likelihood of tipping obeys
i.e. it is zero if the global mean temperature change K but increases linearly with warming above 2 K. While in the real climate system a sharp threshold might not exist, this choice reflects political reality in which policy makers set thresholds for dangerous climate change to be avoided. The constant κtipp is chosen such that in a scenario where the policy maker uses only abatement and remains unaware of possible tipping behaviour, the probability of tipping within 400 years is 50 %. This order of magnitude of the likelihood and damage of tipping is consistent with earlier studies (Cai et al., 2016).
We also take into account the possibility that SRM has to be abolished. While possible reasons remain speculative at this point, it is not inconceivable that SRM has an unexpected destructive side effect, such as a massive deterioration of the ozone layer. We model this by assuming that each year, there is a probability κfail that SRM may not be applied anymore in the future. The cumulative probability of SRM failure over 400 years is 20 %. Failure is assumed irrevocable; once failed, SRM remains unavailable forever. In the basic scenarios (see Sect. 2.3), we include no economic damage related to SRM failure, because humanity is optimistically assumed to realise such dangers and abandon SRM in time (see the realistic storyline scenario in Sect. 3.3 and the high SRM failure damage scenario in Sect. 3.4).
Finally, in the albedo tipping scenario (see Sect. 3.4), we replace the damage tipping point described above by a tipping point which causes an additional radiative forcing (thought of as being due to temperature-driven albedo changes), loosely following Lemoine and Traeger (2014). The forcing obeys
i.e. a positive temperature-dependent forcing occurs if the tipping point is activated and if T exceeds the threshold Talb=1.5 K. The tipping probability obeys Eq. (10) except that the threshold Ttipp is replaced by Talb. Note that this tipping point is reversible in the sense that Falb can decrease again if T decreases.
2.2 Optimisation and performance measures
As in DICE, we assume that all decisions are made by a single policy maker who aims to optimise the welfare of the (homogeneous) world population. As in DICE, welfare depends entirely on consumption. The economic output is spent on investment, I=rY, and global consumption, , where r is the saving rate and L and c are the world population and per capita consumption, respectively. We assume a fixed saving rate of r=22 %. The utility u (which can be thought of as the current happiness of the world population) depends on c: with γ=2 and the quantity to be maximised is the expectation value 𝔼(W) of the welfare W (the time-integrated discounted utility):
where t is (discrete) time and ρ the rate of pure time preference. The greater ρ, the less the far-future count towards W. The morally correct value of ρ has been fiercely discussed (Stern et al., 2007; Lilley, 2012; Ackerman, 2007). Here, we will not join the ethical debate on the correct value, but use the standard value of 1.5 % and perform a sensitivity study with ρ=0.5 (see Sect. 3.5).
The decision variables are the amount of CO2 abatement μ (the fraction of CO2 avoided) and the sulfur injection rate IS. The model is integrated in yearly time steps, but the decision variables μ and IS are changed only once a decade to save computational effort. The policy (sequence of values for μ and IS) is optimised such as to maximise the expected welfare, 𝔼(W), over a time horizon until 2400, though the far future is heavily discounted. The optimisation is performed using dynamic programming (see Appendix). Once an optimal policy is found, it is evaluated by running an ensemble of 5000 members with this policy and Monte Carlo realisations of the stochastic elements (climate tipping and SRM failure). The best policy is the one yielding the highest expected welfare 𝔼(W). For easier comparison, we define a performance measure based on the improvement of W under policy π with respect to a no-action policy ():
where Wπ, W0, and WAD are the expectation values over the Monte Carlo ensemble of the welfare associated with policy π, the no-action case, and the optimal policy for the deterministic abatement-only case (the policy that would be optimal if the decision maker may only use abatement and no climate tipping occurs), respectively. By construction, the relative performance is 100 % for abatement-only scenario in the deterministic case.
Although the objective for the optimisation is the expectation value of the welfare, it is also interesting to investigate the range of possible welfare outcomes, especially the worst-case (or at least relatively bad) scenario. Hence we present two additional performance measures based on the 10th and 90th percentiles of the welfare Wπ. Similar to Eq. (13) we define ζX(π), the X-percentile relative performance of a policy π as
where Wπ,X is the Xth percentile of the welfare (discounted cumulated utility) for policy π. Note that WAD and W0 are still the mean (i.e. not percentiles) welfare associated with the optimal policy for the deterministic abatement-only case, and the no-action case, respectively.
2.3 Scenarios
In Sect. 3.1–3.2 we first consider three stylised policy scenarios. The first is the abatement-only scenario in which the decision maker is allowed to use CO2 abatement but no SRM. The second is SRM-only scenario in which the decision maker uses only SRM until an SRM failure occurs, after which only abatement may be used. This scenario represents a society which does not reduce CO2 emissions but relies entirely on SRM (until it fails). The third is abatement+SRM scenario where the decision maker can use both abatement and SRM, unless SRM fails, after which only abatement is used. A no-policy scenario with neither abatement nor SRM serves as benchmark for performance comparison (see Eqs. 13 and 14). These three standard scenarios are first discussed in a deterministic setting (Sect. 3.1), i.e. in absence of climate tipping and SRM failure, before addressing them in the full model with uncertainty (Sect. 3.2).
While the previous stylised scenarios serve to isolate specific effects, we also present the realistic storyline (see Sect. 3.3), which allows for the fact that it may take time to develop SRM technology, generate a legal framework and public support, and evaluate associated risks. Also, all these processes may fail or the effectiveness of SRM might be found to be too low. Therefore we assume that SRM will become possible only in 2055 and only at 30 % probability. To be precise, at each time step until 2055, there is an equal probability that humanity discovers that SRM is impracticable. In the first decade where SRM is allowed, there is a 20 % probability of SRM failure, 10 % in the second decade, 5 % in the third decade, and 1 % per decade after that, i.e. after some decades of testing, failure becomes less likely. In this scenario, we also investigate the effect of damage in case of SRM failure (“termination shock”): SRM failure is accompanied by a one-time reduction of the GDP by a factor 1−ψfailIS, where IS is the injection rate in megatonnes of sulfur per year (Mt(S) yr−1) and ψfail is given in Table 1.
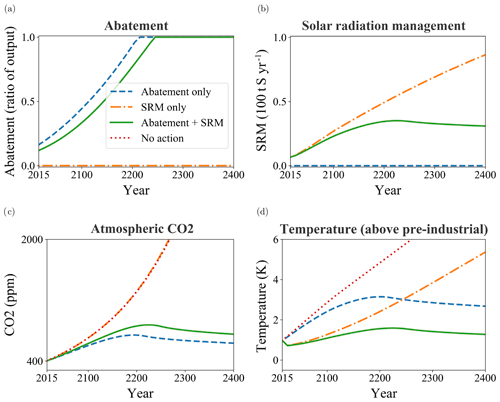
Figure 2Optimal policy and climate model results for the three stylised scenarios in the deterministic setting. (a) Abatement (fraction of CO2 emissions avoided), (b) SRM (Mt(S) yr−1), (c) atmospheric CO2 concentration (ppmv), and (d) global mean temperature above pre-industrial temperature (K). The dashed blue line represents the abatement-only scenario, dashed-dotted orange line represents SRM-only scenario, solid green line represents abatement+SRM scenario, and dotted red line (only panel c and d) represents no climate action (i.e. neither abatement nor SRM).
Table 2Comparison of policies in the deterministic setting (no tipping, no SRM failure). abatement-only scenario means that no SRM is used, SRM-only scenario means that no abatement is used (unless SRM fails see text), and in abatement+SRM scenario both are used. The performance ζ (see Eq. 13) is a measure of the increase in expected cumulated discounted utility w.r.t. the no-action scenario, and is normalised such as to yield 100 % for abatement-only scenario. The column “Peak SRM” contains the highest SRM values (in Mt(S) yr−1) over all time steps. “Ab 50 %” and “Ab 99 %” show the year in which the abatement reaches 50 % and 99 %, respectively. SCC is the social cost of carbon in the first time step (measured in USD (in 2005) per tonne of carbon).

* SRM does not peak but keeps increasing until the upper limit of 100 Mt(S) yr−1. n/a means not applicable.
3.1 The deterministic case
As a reference, we first consider the deterministic case, i.e. without SRM failure and tipping points, in the three stylised scenarios (see Fig. 2 and Table 2). Allowing SRM in addition to abatement delays abatement by 2–3 decades, but does not replace it (Fig. 2a). CO2 concentrations in abatement+SRM scenario (Fig. 2c) peak slightly later than in abatement-only scenario and reach higher values (875 ppmv instead of 741 ppmv). SRM helps to reduce global warming considerably: the global mean temperature change T peaks at 1.6 K for abatement+SRM scenario but at 3.1 K for abatement-only scenario (Fig. 2d). SRM slightly decreases towards the end of the simulation, when CO2 concentration also goes down. This illustrates the potential use of SRM as a transition technology, especially under ambitious abatement: SRM can be used for a limited time in modest strength to cut off a warming overshoot.
In SRM-only scenario, CO2 concentrations reach 2000 ppmv in 2260 and continue to increase (Fig. 2c). Note that currently known fossil fuel reserves are insufficient to generate this much carbon, but it is not impossible that fracking and newly discovered coal deposits will lead to sufficient fuel resources (Cassedy and Grossman, 2017). The temperature increase T continues to rise, reaching 5.4 K in 2400 (Fig. 2d), although it is lower than in the no-action case (neither SRM nor abatement). Due to the sub-linear increase in the radiative forcing with SRM, very high SO2 injection rates would be needed to stabilise T with SRM-only scenario so that the damage related to sulfate injection outweighs the climate damages. Compared to SRM-only scenario, considerably less SRM is needed in abatement+SRM scenario, namely ≈35 Mt(S) yr−1 (Fig. 2b; 3-4 Pinatubo eruptions per year), yet T remains much lower. This suggests that abatement is required in order to achieve long-term temperature stabilisation.
The relative performance ζ(π) for SRM-only and abatement+SRM scenarios becomes 186 % and 238 %, respectively (see Table 2). (By construction, ζ=100 % for abatement-only scenario in the deterministic setting.) The reason for the better performance of SRM-only scenario compared to abatement-only scenario is that SRM-only scenario yields lower temperatures and a higher utility in the first two centuries, which contribute most to the cumulative utility due to discounting. In addition, postponing damage is beneficial as it allows more time for accumulating capital.
3.2 The effect of uncertainties
Table 3Comparison of policies in the stochastic setting, i.e. including climate tipping and SRM failure. No-action case means that neither abatement nor SRM are used; other scenarios are explained in Sect. 2.3. The performance measures ζ, ζ10, and ζ90 are given in Eqs. (13) and (14). The columns “SRM fail” and “Tipping” show the probability that SRM failure or climate tipping occurs before 2415. The column “Peak SRM” contains the highest SRM value (in Mt(S) yr−1) over all time steps and over all ensemble members. This corresponds to members in which no SRM failure or climate tipping occurred, at least before the time of the SRM peak. “Ab 50 %” and “Ab 99 %” show the year in which the abatement reaches 50 % and 99 %, respectively. SCC is the social cost of carbon in the first time step (measured in USD (in 2005) per tonne of carbon).

1 SRM does not peak but keeps increasing until the upper limit of 100 Mt(S) yr−1. 2 Tipping can occur but the policy maker ignores this and chooses the policy which would be optimal in the deterministic (det.) case. n/a means not applicable.
Figure 3Tipping risk and policy in the stochastic setting (i.e. with tipping point and SRM failure). (a) cumulative probability of tipping for abatement-only scenario (blue dashed line), SRM-only scenario (yellow dash-dotted) and abatement+SRM scenario (green solid). (b–l) policy and climate response for the same scenarios (zoomed in on years 2015–2300 to enhance readability), namely abatement-only (d, g, j), SRM-only (b, e, h, k), and abatement+SRM (c, f, i, l) scenarios. Variables shown are SRM deployed (b, c); note the different y-axis scale), abatement fraction (d, e, f), atmospheric CO2 content in ppmv (g, h, i), and global mean temperature change (j, k, l); note the different y-axis scale). The thin blue lines represent a sample of individual ensemble members, the thick red line the ensemble mean, and the blue shaded area indicates the range of possible values in the whole ensemble. The dashed blue line depicts the results from the deterministic case (Fig. 2) for reference.
Next we include the stochastic elements, temperature-induced tipping, and SRM failure, and determine again the optimal policies for each scenario, prior to evaluating the optimal policy by means of a Monte Carlo ensemble (see Sect. 2.2). In Fig. 3b–l, we plot the policy (abatement and SRM), carbon concentration, and temperature for the three stylised scenarios. The plots depict some sample paths of individual Monte Carlo runs (thin blue lines), the range of possible outcomes (shading) and the ensemble mean (red line). For comparison, the results from the deterministic case (compare Fig. 2) are also plotted (dashed blue lines).
In the abatement-only scenario, the danger of tipping initially leads to higher abatement (Fig. 3d) than in the deterministic case, although the temperature is not kept below the 2 K threshold (see Fig. 3j). If tipping occurs, the abatement decreases again as there is no further tipping point to be avoided. (This effect is caused by having a single tipping point which, once activated, does not react to system changes. Compare the Albedo tipping point in Sect. 3.4.) The relative performance is 105 % (see Table 3, row 3), i.e. it slightly improves when the decision maker takes tipping into account (compare Table 3, row 2). Recall that the reference scenario for WAD uses the policy that would be optimal in absence of tipping, i.e. the policy maker ignores climate tipping.
In the abatement+SRM case, the optimal policy closely resembles the deterministic one if no SRM failure occurs (Fig. 3c, f). Without SRM failure, T stays below 2 K (Fig. 3l) and hence no tipping occurs. In case of an SRM failure, the temperature suddenly increases and abatement suddenly increases, as the decision maker now tries to limit the warming (and tipping risk) with only abatement. Note that such a sudden increase in abatement may not be feasible in reality. If climate tipping occurs, abatement is reduced again. Compared to abatement-only scenario, the abatement is delayed by 3–4 decades.
In the SRM-only scenario, the policy again resembles the deterministic case provided no SRM failure occurs and T is below 2 K (Fig. 3b). When T=2 K is reached, SRM increases sharply to reduce the tipping risk. As before, abatement strongly increases after SRM failure, but is reduced slightly if tipping occurs (Fig. 3e). SRM-only scenario has a performance of 181 %, much higher than abatement-only scenario. However, the chance of climate tipping by the year 2415 is considerably higher for SRM-only scenario (61.0 % vs. 37.8 % for abatement-only scenario, see Table 3). As in the deterministic setting, the reason is that initially SRM can control the global warming more effectively than abatement, while abatement is a long-term measure. Hence damage is postponed to the far future which is heavily discounted. The cumulative probability of tipping is lower for SRM-only scenario than for abatement-only scenario until 2350, when the situation reverses (Fig. 3a).
Compared to the deterministic cases, including uncertainty slightly reduces the difference in relative performance between abatement-only scenario and the scenarios using SRM (compare Table 3 vs. Table 2). There are two competing effects: the danger of tipping might favour using SRM, which reduces the tipping probability in the near future, while the possibility of SRM failure reduces the performance of SRM-based scenarios.
In abatement-only scenario, there is a high spread between the relative performance measures ζ, ζ10, and ζ90 compared to SRM-only and abatement+SRM scenarios. This is due to the fact that in most (>90 %) of the ensemble members, SRM keeps global warming below 2 K at least until ≈2200. Hence SRM postpones climate tipping into the far future (except in the few ensemble members with early SRM failure); for abatement-only scenario, tipping can occur as early as 2080. Early tipping greatly reduces the performance because it reduces the GDP for a long period of time and because it is less heavily discounted. For abatement+SRM scenario, only 6.2 % (i.e. <10 %) of the ensemble members show climate tipping, but they strongly affect the mean performance. This explains why, for this scenario, ζ<ζ10.
Although DICE is too limited to give reliable absolute values of the social cost of carbon (SCC) (van den Bergh and Botzen, 2015), comparing scenarios gives qualitative insight into how SRM affects the SCC (Table 2 and Table 3). For abatement-only scenario, the SCC in 2015 is USD 35 per tonne of carbon (in 2005 USD) in the deterministic case and USD 41 per tonne of carbon when including tipping points. For abatement+SRM scenario, the SCC is USD 20 per tonne of carbon (both deterministic and stochastic): SRM lowers the SCC by partially compensating the damage caused by CO2 emissions. For SRM-only scenario, the SCC is only slightly higher, namely USD 21 per tonne of carbon (deterministic) and USD 23 per tonne of carbon (stochastic) because SRM suppresses most climate damage in the near future, which is discounted least.
3.3 Realistic storyline
The previous scenarios were very stylised, in order to isolate the impact of SRM and stochastic elements. However, the actual situation is more complex: presently SRM is not available and we do not know whether it ever will be; yet we might want to decide now whether to pursue (research and development of) SRM. To address this question, we consider a “realistic storyline” scenario in which we assume that SRM will become possible only in 2055, and only at 30 % probability (in the decades before 2055, there is a certain probability each time step that SRM is declared infeasible, e.g. because scientists identify unacceptable environmental risks). We also assume that after 2055, the probability of SRM failure decreases in time, i.e. with ongoing testing, and allow for damage associated with a termination shock in case of SRM failure (see Sect. 2.3). Unlike (irreversible) climate tipping, the termination shock is a short-lived phenomenon and is stronger for extensive SRM.
In those ensemble members where SRM becomes available in 2055, it is used sparingly in the first time step because the probability of failure is still high and the decision maker wants to limit the termination shock. In later time steps, SRM is used only slightly less than in the abatement+SRM scenario, peaking at 31.4 % rather than 35 %. This difference mainly arises because the decision maker wants to reduce the termination shock: if the termination shock damage is omitted from the realistic storyline, SRM peaks at 34.7 %.
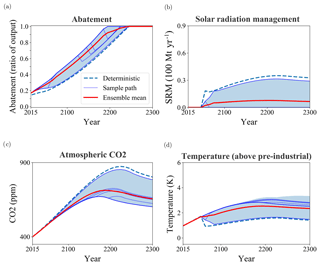
Figure 4Optimal policy and climate development for the realistic storyline scenario. (a) Abatement fraction, (b) SRM in 100 Mt(S) yr−1, (c) atmospheric carbon concentration in ppmv, (d) global mean temperature change w.r.t. pre-industrial temperature. The thin blue lines represent a sample of individual ensemble members, the thick red line the ensemble mean, and the blue shaded area indicates the range of possible values in the whole ensemble. The dashed blue line depicts the results from a deterministic reference case in which SRM becomes available in 2055 certainly and neither SRM failure nor climate tipping occur.
In the first time step (2015), when the decision maker assumes that SRM will become available with 30 % probability only, the abatement μ(2015)=0.17, only slightly less than in the abatement-only scenario where μ(2015)=0.18. For comparison, in a deterministic reference case in which SRM will be available from 2055 certainly, and no SRM failure or tipping occurs, μ(2015)=0.14 (see Fig. 4). As time progresses until 2055, the ensemble members diverge: if SRM is already banned, abatement increases, but if a time step has passed without a ban, the decision maker becomes more optimistic that SRM will become feasible and abatement becomes less ambitious. In ensemble members where SRM becomes available, 50 % abatement is reached 45 years later than in cases where SRM remains impossible. For current policy, however, the most important point is that in 2015 (“now”), a 30 % chance of SRM becoming available does not lead to significant reduction in optimal abatement.
On the other hand, the performance, ζ, of this scenario is 125 % (Table 3), significantly higher than for abatement-only scenario. The lowest 10th percentile performance, ζ10, is very similar to the abatement-only scenario. In the realistic storyline, the low-performance members are those in which SRM never becomes available, and the policy (i.e. trajectory of abatement) in these runs is very similar to abatement-only scenario. However, ζ90 is much higher for the realistic storyline than for abatement-only scenario. This measure is dominated by those members in which SRM becomes available. The total climate tipping risk for the realistic storyline is 30.1 % compared to 37.8 % in the abatement-only scenario. The SCC for the realistic storyline is USD 37 per tonne of carbon, 12 % lower than for abatement-only scenario.
These comparisons between the realistic storyline and abatement-only scenario indicate that the former performs better. This is because in those cases where SRM does become available, the welfare gain of climate policy is twice as high as in the abatement-only case. Therefore, a policy maker in 2015 should not dismiss SRM prematurely, but keep the option open (by encouraging research and development). If we are lucky and SRM works well, it can greatly enhance future welfare, whereas if it never becomes feasible we are not worse off than with abatement-only scenario. (Note, however, that we did not include the possibility of a large-scale SRM test with huge unexpected damage, but assumed careful well-designed research.) However, the prospect of possible future SRM should not lead to a significant reduction in abatement efforts at the current stage.
3.4 SRM as “climate insurance”
In the previous scenarios, SRM was used in a continuous way as a complement for abatement in order to further reduce global warming, especially when the warming was highest. Here we investigate under which circumstances it can be advisable to use SRM as an insurance, i.e. suddenly increase its use or even voluntarily delay using it at all.
First, we consider a situation in which SRM is very dangerous, and thus unattractive to use unless climate change is also very dangerous. This is achieved by assigning a very high, but one-time only, damage to SRM failure, namely reducing capital by a factor in case of SRM failure. Here IS is the injection rate in megatonnes of sulfur per year (Mt(S) yr−1) and IS0=5 Mt(S) yr−1. This means that already at modest injection rates, SRM failure is assumed to cause substantial capital losses. In addition, we increase the likelihood of tipping failure by a factor of 4. Apart from these changes, the scenario is the same as the abatement+SRM scenario in Sect. 3.2. This scenario is not necessarily considered the most likely but serves as a proof of concept. The result is that SRM is not started until the tipping threshold T=2 K threatens to be reached (see Fig. 5a–c). When the threshold is reached, SRM is started and somewhat more SRM is applied than strictly necessary to keep below T+2 K. This is because in our parameterisation, damage levels off somewhat with increasing injection rate, i.e. if SRM is used at all, then a little extra does not make failure costs that much worse. The temperature increase is kept below T=2 K throughout, unless SRM fails. Compared to the standard abatement+SRM case, peak SRM is reduced to 27.6 Mt(S) yr−1, i.e. by about 21 %, and 50 % abatement is reached in 2127, i.e. 12 years earlier. This experiment shows that the possibility of SRM causing high damage can cause a delay in its use until climate change also becomes very dangerous (tipping threshold reached).
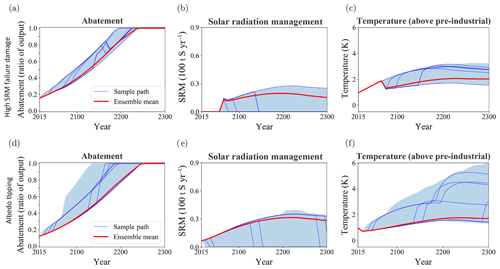
Figure 5Policy and temperature for the “SRM as insurance” scenarios (see Sect. 3.4). The top row shows the scenario with high damage in case of SRM failure, while the bottom row shows the scenario with an albedo tipping point. The left column (a, d) show abatement, the middle one (b, e) SRM, and the right (c, f) warming. The thin blue lines represent a sample of individual ensemble members, the thick red line the ensemble mean, and the blue shaded area indicates the range of possible values in the whole ensemble.
Second, we replace the standard tipping point in abatement+SRM scenario by the “albedo” tipping point (see Sect. 2.1.4). It is found that if the policy maker can use SRM freely, they do not employ it to such a degree as to stay below K but take the (small) chance of crossing the threshold. If this happens, they do increase SRM to counteract the albedo feedback (the bump after 2200 in Fig. 5e). Although the time step for determining policies is 10 years, the albedo feedback is weak enough that no runaway global warming occurs since, with SRM, T−Talb and hence Falb is small. This is why a modest increase suffices to suppress this effect. However, if SRM has failed, temperature is much higher than Talb, increasing both the probability of albedo tipping and the radiative forcing strength if tipping occurs. As in the standard abatement+SRM scenario, the policy maker increases abatement in case of SRM failure to avoid the tipping point. However, if the albedo tipping occurs after SRM failure, the policy maker increases abatement yet again in order to limit the positive temperature feedback. Nonetheless, the albedo tipping can cause additional warming of more than 2 K. A positive climate feedback tipping point can thus lead to enhanced climate policy – SRM or abatement or both – after being triggered, in order to reduce its consequences.
3.5 Sensitivity analysis
Table 4Policy metrics of the sensitivity runs. “Abate 50 %” is the year in which abatement reaches 50 % (μ=0.5). “Peak SRM” (in Mt(S) yr−1) is the highest SRM value of the ensemble (over all times and all members) and corresponds to those ensemble members without early SRM failure or climate tipping. “SCC” is the social cost of carbon in USD(2005) per tonne of carbon. All simulations were preformed in the stochastic settings and are either abatement-only scenario or abatement+SRM scenario (abbreviated here as Ab.+SRM). The first two cases, labelled “standard”, are repeated from Table 3 for convenience. The sensitivity runs correspond to those discussed in Sect. 3.5. n/a means not applicable.

The results of our model substantially depend on the rate of time preference ρ (see Sect. 2.2). In abatement-only scenario, reducing ρ from the standard value of 1.5 % to a lower value of 0.5 % will lead to stronger abatement: 50 % abatement is reached 27 years earlier (see Table 4). This is expected as a lower rate of time preference means that the decision maker gives more weight to the welfare of future generations and is more willing to sacrifice present consumption to reduce climate change. The SCC rises from USD 41 to USD 70 per tonne of carbon. Interestingly, abatement also increases in the abatement+SRM scenario (50 % abatement is reached 23 years earlier) when reducing ρ to 0.5 %, while the peak SRM (definition: see Table 3) decreases by about 11 %. In other words, a decision maker who cares strongly about the future will choose to reduce CO2 emissions rather than forcing future generations to rely on SRM, which causes damages and might fail. The SCC rises from USD 20 to USD 30 per tonne of carbon.
A potentially important limitation of DICE is that abatement costs are exogenous, whereas in reality one would expect costs to decline with growing employment (learning by doing). While fully exploring learning by doing is outside the scope of this study, we estimate the sensitivity to abatement costs in a simulation wherein abatement costs decrease more quickly in time and reach a lower value for t→∞. This is done by putting λ2=1.5 and λ3=0.015 in Eq. (8b), which lowers abatement cost by a factor of about 0.6 after 70 years compared to the standard scenario. The resulting policy shows a faster abatement by about 30 years, leading to a lower peak in atmospheric carbon (745 ppm instead of 870 ppm). Peak SRM is reduced to 29 Mt(S) yr−1, as less SRM is needed if carbon concentrations are lower. Thus the development of abatement cost can significantly affect the need for SRM.
The distribution of the damages between the two major contributors, namely warming and residual climate change, was chosen rather arbitrarily. However, halving ψT (warming contribution) and doubling ψP (residual contribution) does not qualitatively affect our results. A 50 % abatement is reached 4 years later in the abatement+SRM scenario, and SRM peaks at 32.6 Mt(S) yr−1 instead of 35.0 Mt(S) yr−1, i.e. the optimal policy still combines a similar abatement with modest SRM. The SCC drops from USD 20 to USD 17 per tonne of carbon. Lowering the tipping threshold from 2 to 1 K leads to a 2 % increase in peak SRM, while not affecting abatement. Doubling the damages associated with climate tipping () only accelerates 50 % abatement by 3 years in the abatement+SRM case and the SCC remains at USD 20 per tonne of carbon. Doubling the likelihood of climate tipping (κtipp) accelerates 50 % abatement by 2 years and likewise does not affect SCC. Increasing the failure probability of SRM (κfail) by a factor of 4, i.e. such that SRM failure occurs in 80 % of the ensemble members rather than 20 %, increases the SCC only by 15 % in the abatement+SRM scenario, i.e. from USD 20 to USD 23 per tonne of carbon. The reason is that the likelihood of SRM failure in the first decades, which are least discounted, is still fairly small. The peak SRM is reduced only by 2 %: as long as SRM is available, it is used despite high failure probability. A 50 % abatement is reached in 2121, rather than 2138, in the ensemble mean. Doubling the damage associated with SRM (i.e. doubling ψS) accelerates 50 % abatement by 6 years and the SCC rises from USD 20 to USD 22 per tonne of carbon. The peak SRM is reduced by about 23 %, to 26.8 Mt(S) yr−1. Likewise, halving ψS increases peak abatement by 25 %. Hence even if SRM is twice (or half) as damaging as assumed in the standard case, the optimal policy still employs modest SRM as a complement to abatement.
To summarise, changes in the damage function and/or likelihood of stochastic events do not qualitatively affect the optimal policy in the abatement+SRM scenario, which consists of a combination of reasonably high abatement (delayed by a few decades w.r.t. abatement-only scenario in the standard settings) and modest SRM.
In this paper, we present the first cost–benefit analysis of SRM under uncertainty performed with a rigorous optimisation approach (dynamic programming). From our analysis we draw two conclusions. First, sulfate SRM has the potential to greatly enhance future welfare and should therefore be taken seriously as a possible policy option. Second, even if successful, SRM does not replace CO2 abatement, but complements it. In particular, a policy maker who puts great value on the welfare of future generations (i.e. uses a low rate of pure time preference) will accelerate abatement efforts, which have a long-term benefit rather than forcing later generations to rely on SRM. Apart from smoothly reducing peak warming, SRM might also have a role to play as emergency measure, e.g. in case of emerging positive warming feedbacks or unforeseen strong climate-induced damages. However, this might be a risky approach if SRM itself is potentially associated with strong damages.
Compared to previous studies (Goes et al., 2011; Moreno-Cruz and Keith, 2013; Heutel et al., 2018), our results are more optimistic about SRM, which seems partly due to the improved methodology we adopted. For instance, demonstrating that welfare is severely impacted if the decision maker makes wrong assumptions on the SRM-related damages (Bahn et al., 2015) is not a consistent cost–benefit analysis. The analysis by Goes et al. (2011) only considers a full replacement of abatement by SRM rather than a complementary approach. Compared to Heutel et al. (2018), we find a much stronger reduction in the SCC. However, as discussed previously, their model and optimisation method differ in some crucial points from ours. In particular, Heutel et al. (2018) assume that the implementation cost and damage associated with SRM depend on the fraction of CO2-induced radiative forcing that is balanced by SRM – no matter how high the CO2 concentration is – rather than letting costs and damage depend on the amount of sulfur injected. Therefore at high (low) CO2 concentrations, they obtain a much higher (lower) radiative forcing effect from SRM for the same price, which makes SRM more (less) attractive. In their deterministic simulation, they compensate 50 % of the peak CO2-induced radiative forcing of 6 W m−2, which in our model settings would require an injection rate of 27 Mt(S) yr−1 – about 80 % of our peak injection rate of 35 Mt(S) yr−1 in the deterministic abatement+SRM scenario. However, for the first century, Heutel et al. (2018) use considerably less SRM because they overestimate the price by ignoring that much lower injection rates are needed while CO2 concentrations are low. So overall they use too little SRM and therefore end up with higher temperatures (about 2.5 K peak warming) and a higher SCC.
Our results should not be interpreted as precise policy recommendations to set, for example, exact values of the SCC, as our model is too limited to offer more than a qualitative exploration and comparison of simple scenarios. For example, uncertainty in the climate system is limited to one tipping point, while uncertainty in the climate sensitivity is ignored. Our climate model is based on linear response theory and although this approach captures many climate feedbacks adequately, it does not capture the possible dependence of the response on the background state, e.g. a saturation of carbon sinks (Aengenheyster et al., 2018).
A controversial component in integrated assessment models such as DICE is the quantification of climate damages (Howard, 2014; van den Bergh and Botzen, 2015), which is highly aggregated and based on very limited data. We introduced additional parameters to the damage function by making a plausible, but rather ad hoc, attribution of climate damages to temperature, global precipitation (“residual climate change”), and CO2 concentrations. Also, little is known about the size of ecological, let alone economic, damages associated with SRM. Gaining a better understanding of these damages, and those related to climate change, is essential for conducting a meaningful cost–benefit analysis and ultimately determining a climate policy, hence it should be given a high priority.
The abatement sector of DICE also has important limitations. First, technological improvement is exogenous (abatement costs decrease in time at a prescribed rate) rather than including learning by doing (costs decrease with technology employment). This means that in DICE it is advantageous to wait for the later cost reduction, rather than starting early to bring abatement price down through learning. In addition, DICE assumes that abatement is always costly, whereas in fact the energy transition might rather be a big investment: once the infrastructure is installed, green energy might be cost-competitive with fossil fuels. Both effects likely bias our results against early abatement. A faster (still exogenous) decrease in abatement costs was found to lead to faster abatement and reduced peak SRM.
Our model does not include negative emission techniques, which might provide an important alternative to SRM. Neither does it include active adaptation. The trade-off between negative emissions, adaptation, and SRM would be interesting to study with a more detailed model. Finally, DICE assumes a homogenous economy and a single decision maker. In reality, the damages and benefits of SRM are likely unevenly distributed, with potential for solitary actions and conflict, which was not studied here.
Despite the large scientific and political uncertainties which need to be overcome, we believe that one cannot afford to dismiss SRM at the current stage as it has the potential to greatly reduce climate risk and enhance future welfare. However, the scientific uncertainties, especially concerning efficiency and damages of SRM, and the extent to which SRM can mitigate damages inflicted by global warming must be better quantified. For the time being, the uncertain prospect of SRM becoming available should not tempt us to reduce abatement.
The code used (described in the Methods section) is available upon request from the corresponding author.
A1 Terminal function
Unrealistic behaviour occurs in the last time steps of an optimisation problem because the decisions made do not influence the future anymore (as the future is not simulated). To avoid this problem, we follow Cai et al. (2016) and run the optimisation over 600 years, only considering the first 400 as actual simulation and the final 200 years as “terminal function”. During termination, tipping can still occur and SRM can be freely chosen, while abatement is set to 1. Due to discounting, the trajectory after 600 years has little relevance for the optimal policy during the first 400 years. Indeed, prolonging the runs to 800 years had a negligible effect on policies during the first 400 years.
A2 Optimisation method
The social planner problem aims at finding the policy that maximises the expected cumulative discounted utility. To solve this problem in the stochastic setting, we apply dynamic programming (Bellman, 1957). This methodology relies on the concept of the value function to obtain the optimal policy via backward reduction. As our state space is continuous and no analytic solution is available, we are forced to adopt some approximation scheme to represent the value function at each time step. Following Cai et al. (2016), we use a Chebyshev approximation, which is well suited for parallelisation. The Chebyshev polynomial is obtained by solving a small optimisation problem at each of a finite number of regularly spaced Chebyshev approximation nodes. We used a fourth-degree Chebyshev polynomial with five approximation nodes per continuous dimension. In combination with the binary state variables for the tipping point and SRM failure, this results in 312 500 approximation nodes per time step. This method is developed and discussed extensively in the work by Cai (2009) and Cai et al. (2012a, 2016). For a complete overview we refer the reader to these papers and the references therein. Here we outline the methodological choices specific to the present application: the boundaries used for the domain of the Chebyshev polynomial and adjustments to the value function approximation to accommodate the asymmetry and non-smoothness of the true value function. Additionally, we examine the accuracy of this methodology when applied in the current setting.
A2.1 Boundaries
In order to define the Chebyshev approximation nodes, we must first set the boundaries of the region of state space in which we are interested. To do this, we calculate three trajectories in the deterministic model: first the optimal trajectory (obtained by optimising the whole system in all decision variables with standard deterministic optimisation software); second a “high-emission” trajectory calculated by setting mitigation and SRM to zero for the whole run; and third a “low-emission” trajectory calculated by setting mitigation to one and SRM to zero for the whole run. We subsequently take as domain boundaries for each variable the minimum and maximum over these three trajectories, with an additional margin of minus and plus 30 % of these values. For all experiments, we check that all the sample paths in the ensemble remained well within the boundaries of the domain. For approximation nodes close to the boundaries, it will still be possible to select actions that may bring the system outside the boundaries in the next step. Since a Chebyshev polynomial cannot be extrapolated outside its domain, we first project the state onto the region of interest before evaluating the approximate value function.
A2.2 Value function smoothing
In the current setting, directly using a Chebyshev polynomial to approximate the value function gives poor results because the value function exhibits an asymmetry and a non-smoothness that a low-degree Chebyshev polynomial cannot capture. The discontinuity is caused by the fact that in states with positive temperatures, SRM is available to reduce them, while in states with negative temperatures this is impossible; therefore, positive temperature deviations are preferred over negative temperature deviations of equal magnitude. This problem is resolved by allowing reverse SRM, which generates a radiative forcing of the same magnitude but opposite sign as regular SRM. Allowing such actions changes the value of certain states, thus removing the asymmetry. This is a purely mathematical construct (we do not assume such reverse SRM is actually possible): the states with modified values are never reached in actual trajectories, and are only considered in the first place because the domain of the Chebyshev approximation must be a hypercube.
The non-smoothness results from the fact that the tipping point can only be crossed after a certain threshold is reached: this generates a discontinuity in the first derivative of the value function. This is resolved by fitting two separate Chebyshev polynomials to the two parts of the value function.
A2.3 Accuracy
We test the accuracy of our optimisation by comparing the resulting policy in a deterministic setting to the policy obtained by regular non-linear optimisation. The difference in action and trajectory is <3 %, while the difference in the SCC is <2 %. For the scenario in which only abatement is allowed, errors are lower (0.1 %–1 % for actions and SCC, 0.01 %–0.1 % for trajectories), which is in line with the accuracy reported by Cai et al. (2016). Good accuracy in the deterministic setting may not generalise to the stochastic setting when the stochasticity itself introduces issues. To guard against this problem we ensure that the value function approximation fits well to the actual value function samples obtained at each time step.
All authors conceived the research. CEW and KGH designed the model and scenarios and interpreted results. KGH performed simulations. All authors contributed to writing the paper.
The authors declare that they have no conflict of interest.
Claudia E. Wieners is supported by the Complexity Lab Utrecht (CLUe) of the Centre for Complex Systems Studies at Utrecht University. Henk A. Dijkstra acknowledges support by the Netherlands Earth System Science Centre (NESSC), financially supported by the Ministry of Education, Culture and Science (OCW) (grant no. 024.002.001).
This paper was edited by Ben Kravitz and reviewed by Michael MacCracken and one anonymous referee.
Ackerman, F.: Debating Climate Economics: The Stern Review vs. Its Critics, Report to Friends of the Earth-UK, 1–25, 2007. a
Aengenheyster, M., Feng, Q. Y., van der Ploeg, F., and Dijkstra, H. A.: The point of no return for climate action: effects of climate uncertainty and risk tolerance, Earth Syst. Dynam., 9, 1085–1095, https://doi.org/10.5194/esd-9-1085-2018, 2018. a, b, c
Ahlm, L., Jones, A., Stjern, C. W., Muri, H., Kravitz, B., and Kristjánsson, J. E.: Marine cloud brightening – as effective without clouds, Atmos. Chem. Phys., 17, 13071–13087, https://doi.org/10.5194/acp-17-13071-2017, 2017. a
Andrews, T., Forster, P. M., Boucher, O., Bellouin, N., and Jones A.: Precipitation, radiative forcing and global temperature change, Geophys. Res. Lett., 37, L14701, https://doi.org/10.1029/2010GL043991, 2010. a, b
Auffhammer, M.: Quantifying Economic Damages from Climate Change, J. Econ. Persp., 32, 33–52, https://doi.org/10.1257/jep.32.4.33, 2018. a
Bahn, O., Chesney, M., Gheyssens, J., Knutti, R., and Pana, A. C.: Is there room for geoengineering in the optimal climate policy mix?, Environ. Sci. Policy, 48, 67–76, https://doi.org/10.1016/j.envsci.2014.12.014, 2015. a, b
Bellman, R.: Dynamical Programming, Princeton University Press, Princeton, NJ, USA, 1957. a, b
Brovkin, V., Petoukhov, V., Claussen, M., Bauer, E., Archer, D., and Jaeger, C.: Geoengineering climate by stratospheric sulfur injections: Earth system vulnerability to technological failure, Climatic Change, 92, 243–259, https://doi.org/10.1007/s10584-008-9490-1, 2009. a
Cai, Y.: Dynamic Programming and its Application in Economics and Finance, PhD Thesis, Stanford University, 2009. a
Cai, Y., Judd, K. L., and Lontzek, T. S.: DSICE: A Dynamic Stochastic Integrated Model of Climate and Economy, RDCEP Working Paper No. 12-02, SSRN, https://doi.org/10.2139/ssrn.1992674, 2012. a, b, c
Cai, Y., Judd, K. L., and Lontzek, T. S.: Continuous-Time Methods for Integrated Assessment Models, Working Paper 18365, National Bureau of Economic Research, available at: http://www.nber.org/papers/w18365, last access: May 2012. a
Cai, Y., Judd, K. L., Lenton, T. M., Lontzek, T. S., and Narita, D.: Environmental tipping points significantly affect the cost-benefit assessment of climate policies, P. Natl. Acad. Sci. USA, 112, 4606–4611, https://doi.org/10.1073/pnas.1503890112, 2015. a
Cai, Y., Lenton, T. M., and Lontzek, T. S.: Risk of multiple interacting tipping points should encourage rapid CO2 emission reduction, Nat. Clim. Change, 6, 520–525, https://doi.org/10.1038/nclimate2964, 2016. a, b, c, d, e, f, g, h
Cassedy, E. S. and Grossmann, P. Z.: Introduction to Energy – Resources, Technology, and Society, Third edition, Cambdrige University Press, Cambridge, UK, 2017. a, b
Ciais, P., Sabine, C., Bala, G., Bopp, L., Brovkin, V., Canadell, J., Chhabra, A., DeFries, R., Galloway, J., Heimann, M., Jones, C., Le Quéré, C., Myneni, R. B., Piao, S., and Thornton, P.: Carbon and Other Biogeochemical Cycles, in: Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013. a, b, c
Crutzen, P. J.: Albedo enhancement by stratospheric sulfur injections: A contribution to resolve a policy dilemma?, Climatic Change, 77, 211–219, https://doi.org/10.1007/s10584-006-9101-y, 2006. a
Effiong, U. and Neitzel, R. L.: Assessing the direct occupational and public health impacts of solar radiation management with stratospheric aerosols, Environ. Health, 15, 1–9, https://doi.org/10.1186/s12940-016-0089-0, 2016. a
Gabriel, C. J., Robock, A., Xia, L., Zambri, B., and Kravitz, B.: The G4Foam Experiment: global climate impacts of regional ocean albedo modification, Atmos. Chem. Phys., 17, 595–613, https://doi.org/10.5194/acp-17-595-2017, 2017. a
Goes, M., Tuana, N., and Keller, K.: The economics (or lack thereof) of aerosol geoengineering, Climatic Change, 109, 719–744, https://doi.org/10.1007/s10584-010-9961-z, 2011. a, b, c
Heutel, G., Moreno-Cruz, J., and Shayegh, S.: Climate tipping points and solar geoengineering, J. Econ. Behav. Organ., 132, 19–45, https://doi.org/10.1016/j.jebo.2016.07.002, 2016. a, b, c
Heutel, G., Moreno-Cruz, J., and Shayegh, S.: Solar Geoengineering, Uncertainty, and the Price of Carbon, J. Environ. Econ. Manag., 87, 24–41, https://doi.org/10.1016/j.jeem.2017.11.002, 2018. a, b, c, d, e, f, g, h, i
Howard, P.: Omitted Damages: What's missing from the Social Cost of Carbon, available at: https://costofcarbon.org/files/Omitted_Damages_Whats_Missing_From_the_Social_Cost_of_Carbon.pdf (last access: 27 November 2017), 2014. a
IPCC, 2014: Climate Change 2014: Impacts, Adaptation, and Vulnerability, Part A: Global and Sectoral Aspects, Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, 2014. a
Irvine, P. J., Kravitz, B., Lawrence, M. G., Gerten, D., Caminade, C., Gosling, S. N., Hendy, E. J., Kassie, B. T., Kissling, W. D., Muri, H., Oschlies, A., and Smith, S. J.: Towards a comprehensive climate impacts assessment of solar geoengineering, Earth's Future, 5, 93–106, https://doi.org/10.1002/2016EF000389, 2017. a
Joos, F., Roth, R., Fuglestvedt, J. S., Peters, G. P., Enting, I. G., von Bloh, W., Brovkin, V., Burke, E. J., Eby, M., Edwards, N. R., Friedrich, T., Frölicher, T. L., Halloran, P. R., Holden, P. B., Jones, C., Kleinen, T., Mackenzie, F. T., Matsumoto, K., Meinshausen, M., Plattner, G.-K., Reisinger, A., Segschneider, J., Shaffer, G., Steinacher, M., Strassmann, K., Tanaka, K., Timmermann, A., and Weaver, A. J.: Carbon dioxide and climate impulse response functions for the computation of greenhouse gas metrics: a multi-model analysis, Atmos. Chem. Phys., 13, 2793–2825, https://doi.org/10.5194/acp-13-2793-2013, 2013. a, b, c, d
Keller, D. P., Feng, E. Y., and Oschlies, A.: Potential climate engineering effectiveness and side effects during a high carbon dioxide-emission scenario, Nat. Commun., 5, 3304, https://doi.org/10.1038/ncomms4304, 2014. a
Kleinschmitt, C., Boucher, O., and Platt, U.: Sensitivity of the radiative forcing by stratospheric sulfur geoengineering to the amount and strategy of the SO2injection studied with the LMDZ-S3A model, Atmos. Chem. Phys., 18, 2769–2786, https://doi.org/10.5194/acp-18-2769-2018, 2018. a, b, c
Kravitz, B., Caldeira, K., Boucher, O., Robock, A., Rasch, P. J., Alteskjær, K., Bou Karam, D., Cole, J. M. S., Curry, C. L., Haywood, J. M., Irvine, P. J., Ji, D., Jones, A., Kristjánsson, J. E., Lunt, D. J., Moore, J. C., Niemeier, U., Schmidt, H., Schulz, M., Singh, B., Tilmes, S., Watanabe, S., Yang, S., and Yoon, J.-H.: Climate model response from the Geoengineering Model Intercomparison Project (GeoMIP), J. Geophys. Res.-Atmos. 118, 8320–8332, https://doi.org/10.1002/jgrd.50646, 2013. a
Kravitz, B., MacMartin, D. G., Rasch, P. J., and Jarvis, A. J.: A new method of comparing forcing agents in climate models, J. Climate, 28, 8203–8218, https://doi.org/10.1175/JCLI-D-14-00663.1, 2015. a
Latham, J., Rasch, P., Chen, C.-C., Kettles, L., Gadian, A., Gettelman, A., Morrison, H., Bower, K., and Chourlaton, T.: Global temperature stabilization via controlled albedo enhancement of low-level maritime clouds, Philos. T. R. Soc. A, 366, 3969–3987, https://doi.org/10.1098/rsta.2008.0137, 2008. a
Lemoine, D. and Traeger, C., Watch Your Step: Optimal Policy in a Tipping Climate, Am. Econ. J.-Econ. Polic., 6, 137–166, 2014. a
Le Quéré, C., Andrew, R. M., Friedlingstein, P., Sitch, S., Pongratz, J., Manning, A. C., Korsbakken, J. I., Peters, G. P., Canadell, J. G., Jackson, R. B., Boden, T. A., Tans, P. P., Andrews, O. D., Arora, V. K., Bakker, D. C. E., Barbero, L., Becker, M., Betts, R. A., Bopp, L., Chevallier, F., Chini, L. P., Ciais, P., Cosca, C. E., Cross, J., Currie, K., Gasser, T., Harris, I., Hauck, J., Haverd, V., Houghton, R. A., Hunt, C. W., Hurtt, G., Ilyina, T., Jain, A. K., Kato, E., Kautz, M., Keeling, R. F., Klein Goldewijk, K., Körtzinger, A., Landschützer, P., Lefèvre, N., Lenton, A., Lienert, S., Lima, I., Lombardozzi, D., Metzl, N., Millero, F., Monteiro, P. M. S., Munro, D. R., Nabel, J. E. M. S., Nakaoka, S.-I., Nojiri, Y., Padin, X. A., Peregon, A., Pfeil, B., Pierrot, D., Poulter, B., Rehder, G., Reimer, J., Rödenbeck, C., Schwinger, J., Séférian, R., Skjelvan, I., Stocker, B. D., Tian, H., Tilbrook, B., Tubiello, F. N., van der Laan-Luijkx, I. T., van der Werf, G. R., van Heuven, S., Viovy, N., Vuichard, N., Walker, A. P., Watson, A. J., Wiltshire, A. J., Zaehle, S., and Zhu, D.: Global Carbon Budget 2017, Earth Syst. Sci. Data, 10, 405–448, https://doi.org/10.5194/essd-10-405-2018, 2018. a
Lilley, P.: The Failings of the Stern Review of the Economics of Climate Change, The Global Warming Policy Foundation (GWPF) Report 92012, 2012. a
MacMartin, D. G. and Kravitz, B.: Dynamic climate emulators for solar geoengineering, Atmos. Chem. Phys., 16, 15789–15799, https://doi.org/10.5194/acp-16-15789-2016, 2016. a, b, c, d, e, f
Matthews, H. D. and Caldeira, K.: Transient climate-carbon simulations of planetary geoengineering, P. Natl. Acad. Sci. USA, 104, 9949–9954, https://doi.org/10.1073/pnas.0700419104, 2007. a
McClellan, J., Keith, D., and Apt, J.: Cost analysis of stratospheric albedo modification delivery systems, Environ. Res. Lett., 7, 034019, https://doi.org/10.1088/1748-9326/7/3/034019, 2010. a, b, c
Moreno-Cruz, J. B. and Keith, D. W.: Climate policy under uncertainty: A case for solar geoengineering, Climatic Change, 121, 431–444, https://doi.org/10.1007/s10584-012-0487-4, 2013. a, b
Moriyama, R., Sugiyama, M., Kurosawa, A., Masuda, K., Tsuzuki, K., and Ishimoto, Y.: The cost of stratospheric climate engineering revisited, Mitig. Adapt. Strateg. Glob. Change, 22, 1207, https://doi.org/10.1007/s11027-016-9723-y, 2017. a, b, c
Myhre, G., Shindell, D., Bréon, F.-M., Collins, W., Fuglestvedt, J., Huang, J., Koch, D., Lamarque, J.-F., Lee, D., Mendoza, B., Nakajima, T., Robock, A., Stephens, G., Takemura, T., and Zhang, H: Anthropogenic and Natural Radiative Forcing, in: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013.
Niemeier, U. and Timmreck, C.: What is the limit of climate engineering by stratospheric injection of SO2?, Atmos. Chem. Phys., 15, 9129–9141, https://doi.org/10.5194/acp-15-9129-2015, 2015. a, b, c
Niemeier, Niemeier, U. and Schmidt, H.: Changing transport processes in the stratosphere by radiative heating of sulfate aerosols, Atmos. Chem. Phys., 17, 14871–14886, https://doi.org/10.5194/acp-17-14871-2017, 2017. a
Nordhaus, W. D.: The “DICE” Model: Background and Structure of a Dynamic Integrated Climate–Economy Model of the Economics of Global Warming, Cowles Foundation Discussion Paper No. 1009, Cowles Foundation for Research in Economics: New Haven, CT, 1992. a, b, c, d
Nordhaus, W. D. and Boyer, J.:, Warming the World – Economic models of Global Warming, The MIT Press, 2000. a, b
Nordhaus, W. D.: Evolution of Modeling of the Economics of Global Warming: Changes in the DICE model, 1992–2017, Climate Change, 148, 623–40, https://doi.org/10.1007/s10584-018-2218-y, 2018. a, b, c
Pindyck, R. S.: The Use and Misuse of Models for Climate Policy, Rev. Env. Econ. Policy, 11, 100–114, https://doi.org/10.1093/reep/rew012, 2017. a
Pitari, G., Aqula, V., Kravitz, B., Robock, A., Watanabe, S., Cionni, I., De Luca, N., Di Genova, G., Mancini, E., and Tilmes, S.: Stratospheric ozone response to sulphate geoengineering: Results from the Geoengineering Model Intercomparison Project (GeoMIP), J. Geophys. Res.-Atmos., 119, 2629–2653, https://doi.org/10.1002/2013JD020566, 2014. a
Robock, A.: Volcanic eruptions and climate, Rev. Geophys., 38, 191–219, https://doi.org/10.1029/1998RG000054, 2000. a
Robock, A., Marquardt, A., Kravitz, B., and Stenchikov, G.: Benefits, risks, and costs of stratospheric geoengineering, Geophys. Res. Lett., 36, L19703, https://doi.org/10.1029/2009GL039209, 2009. a, b
Seneviratne, S. I., Phipps, S. J., Pitman, A. J., Hirsch, A. L., Davin, E. L., Donat, M. G., Hirschi, M., Lenton, A., Wilhelm, M., and Kravitz, B.: Land radiative management as contributor to regional-scale climate adaptation and mitigation, Nat. Geosci., 11, 88–96, https://doi.org/10.1038/s41561-017-0057-5, 2018. a
Stenchikov, G. L., Kirchner, I., Graf, H.-F., Antuña, J. C., Grainger, R. G., Lambert, A., and Thomason, H: Radiative forcing from the 1991 Mount Pinatubo volcanic eruption, J. Geophys. Res., 103, 13837–13857, https://doi.org/10.1029/98JD00693, 1998. a
Stern, V., Peters, S., Bakhshi, V., Bowen, A., Cameron, C., Catovsky, S., Crane, D., Cruickshank, S., Dietz, S., Edmondson, N., Garbett, S.-L., Hamid, L., Hoffman, G., Ingram, D., Jones, B., Patmore, N., Radcliffe, H., Sathiyarajah, R., Stock, M., Taylor, C., Vernon, T., Wanjie, H., and Zenghelis, D.: The Stern Review, Government Equalities Office, Home Office, 2007. a
Stowe, L. L., Carey, R. M., and Pellegrino, P. P.: Monitoring the Mt. Pinatubo aerosol layer with NOAA/11 AVRHH DATA, Geophys. Res. Lett. 19, 159–162, https://doi.org/10.1029/91GL02958, 1992. a, b
Thompson, W. J., Wallace, J. M., Jones, P. D., and Kennedy, J. J.: Identifying Signatures of Natural Climate Variability in Time Series of Global-Mean Surface Temperature: Methodology and Insights, J. Climate, 22, 6120–6141, https://doi.org/10.1175/2009JCLI3089.1, 2009. a, b
Tilmes, S., Richter, J., Kravitz, B., MacMartin, D. G., Mills, M. J., Simpson, I. R., Glanville, A. S., Fasullo, J. T., Phillips, A. S., Lamarque, J.-F., Tribbia, J., Edwards, J., Mickelson, S., and Ghosh, S.: CESM1(WACCM) Stratospheric Aerosol Geoengineering Large Ensemble (GLENS) project, B. Am. Meteorol. Soc., 99, 2361–2371, https://doi.org/10.1175/BAMS-D-17-0267.1, 2018. a
Tjiputra, J. F., Grini, A., and Lee, H.: Impact of idealized future stratospheric aerosol injection on the large-scale ocean and land carbon cycles, J. Geophys. Res.-Biogeo., 121, 2–27, https://doi.org/10.1002/2015JG003045, 2016. a
Trisos, C. H., Amatulli, G., Gurevitsh, J., Robock, A., Xia, L., and Zambri, B.: Potentially dangerous consequences for biodiversity of solar geoengineering implementation and termination, Nat. Ecol. Evol. 2, 475–482, https://doi.org/10.1038/s41559-017-0431-0, 2018. a
UNFCCC: Adoption of the Paris Agreement, United Nations Framework Convention on Climate Change, United Nations Office, Geneva, Switzerland, 2015. a
van den Bergh, J. C. J. M. and Botzen, W. J. W.: Monetary valuation of the social cost of CO2 emissions: a critical survey, Ecol. Econ., 114, 33–46, https://doi.org/10.1016/j.ecolecon.2015.03.015, 2015. a, b
Visioni, D., Pitari, G., and Aquila, V.: Sulfate geoengineering: a review of the factors controlling the needed injection of sulfur dioxide, Atmos. Chem. Phys., 17, 3879–3889, https://doi.org/10.5194/acp-17-3879-2017, 2017. a
Ward, P. L.: Sulphur dioxide initiates global climate change in four ways, Thin Solid Films, 517, 3188–3203, https://doi.org/10.1016/j.tsf.2009.01.005, 2009. a, b
World Bank: available at: https://data.worldbank.org/indicator/NY.GDP.MKTP.KD (last access: 5 July 2019), 2017. a





