the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
ESD Ideas: Propagation of high-frequency forcing to ice age dynamics
Mikhail Y. Verbitsky
Michel Crucifix
Dmitry M. Volobuev
Palaeoclimate records display a continuous background of variability connecting centennial to 100 kyr periods. Hence, the dynamics at the centennial, millennial, and astronomical timescales should not be treated separately. Here, we show that the nonlinear character of ice sheet dynamics, which was derived naturally from the ice-flow conservation laws, provides the scaling constraints to explain the structure of the observed spectrum of variability.
Most theories of Quaternary climates consider that glacial–interglacial cycles emerge from components of the climate system interacting with each other and responding to the forcing generated by the variations in summer insolation caused by climatic precession and the changes in obliquity and in eccentricity. A common approach is to represent these interactions and responses by ordinary differential equations. In a low-order dynamical system, the state vector only includes a handful of variables, which vary on roughly the same timescales as the forcing. Barry Saltzman has long promoted this approach, and his models' state variables represented the volume of continental ice sheets, deep ocean temperature, carbon dioxide concentration, and in some models the lithospheric depression (e.g., Saltzman and Verbitsky, 1993). Similar models featuring other mechanisms were published more recently (e.g., Omta et al., 2016). The purpose of these models is to explain the temporal structure of ice age cycles, but the spectrum of variability at centennial and millennial timescales is generally ignored. This approach is commonly justified by a hypothesis of the separation of timescales, as formulated by Saltzman (1990). However, this hypothesis is questionable. Indeed, the observational records display a continuous background of variability connecting centennial to 100 kyr periods (Huybers and Curry, 2006). For this reason, the dynamics at the centennial, millennial, and astronomical timescales should not be considered separately. Here, we address this concern and show that the ice dynamics are an effective vehicle for propagating high-frequency forcing upscale.
To make this case, we use the dynamical model previously presented in Verbitsky et al. (2018). This nonlinear dynamical system was derived from scaled conservation equations of ice flow, combined with an equation describing the evolution of a variable synthesizing the state of rest of the climate, called “climate temperature”. The three variables are thus the area of glaciation, ice sheet basal temperature, and climate temperature. Without astronomical forcing, the system evolves to an equilibrium. When the astronomical forcing is present, the system exhibits different modes of nonlinearity leading to different periods of ice age rhythmicity. Specifically, when the ratio of positive climate feedback to negative glaciation feedback (quantified by the V number) is about 0.75, the system displays glacial–interglacial cycles of a period of roughly 100 kyr. In effect, the response doubles the obliquity period. For this mechanism to operate, ice needs to survive through a first maximum of insolation and then grow to a level at which it is vulnerable to an – even modest – increase in insolation. In the Verbitsky et al. (2018) model with reference parameters, the threshold corresponds to a glaciation area S of roughly 20×106 km2.
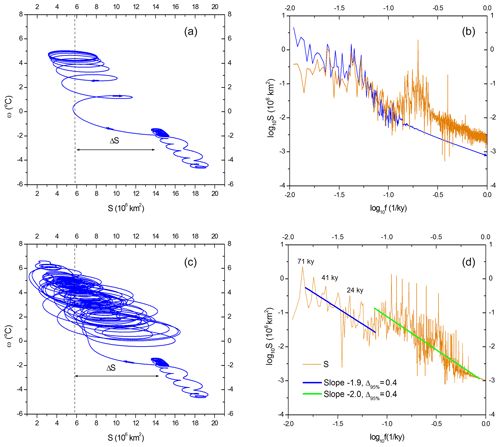
Figure 1(a) The system response to pure 5 kyr sinusoid of variable amplitude on a phase plane of glaciation area S (106 km2) vs. climate temperature ω (∘C); ΔS is the disruption potential; (b) the blue line represents the reference system response to astronomical forcing (Verbitsky et al., 2018). Millennial forcing is absent here. The brown line shows the system response when the orbital forcing is combined with 5 kyr sinusoid of the 10-fold amplitude. The diagram is a linear amplitude spectrum on a logarithmic scale; the vertical axis measures the amplitude of glacial area variations, log10[(106 km2)]; the horizontal axis is log10[f(1 kyr−1)]; (c) same as (a) but millennial forcing is formed by seven sinusoids of the same amplitude (∼2.5 of the insolation forcing amplitude) and periods of 3, 4, 5, 6, 7, 8, and 9 kyr. (d) Same as (b) for multi-period forcing of (c).
In the reference experiment presented in Verbitsky et al. (2018), the system is driven, following standard practice, by mid-June insolation at 65∘ N (Berger and Loutre, 1991). The output of three additional experiments is shown here. In the first experiment, the mid-June insolation is replaced with a sinusoid of 5 kyr period and variable amplitude (first, about the same amplitude as of insolation forcing and then increased 10-fold). In the second experiment, this 10-fold increased 5 kyr period sinusoid is combined with mid-June insolation at 65∘ N. In the third experiment, the forcing is represented by several sinusoids of smaller amplitudes (∼2.5 of the insolation forcing amplitude) and periods spread between 3 and 9 kyr. The results demonstrate the following.
- a.
When our system is forced by a pure 5 kyr sinusoid of small amplitude, the system remains in the vicinity of its equilibrium point, with a glaciation area of 15×106 km2 and a climate temperature of −2 ∘C (cf. Fig. 1a). When the amplitude of the sinusoid is increased 10-fold, the effects of the negative phases of the forcing are no longer symmetric to those of the positive phases because of the system's nonlinearity. As a consequence, the system moves to a different phase-plane domain, around 6×106 km2 of glaciation area, and a climate temperature of 4.6 ∘C (Fig. 1a).
- b.
This shift of the time mean glaciation area and temperature has a dramatic effect on ice age dynamics. When insolation forcing is combined with strong millennial forcing, the latter moves the system into the domain where obliquity period doubling no longer occurs because ice no longer grows to the level needed to enable the strong positive deglaciation feedback. Consequently, the 100 kyr variability almost vanishes – Fig. 1b. We term this suppression of ice age variability by millennial variability “hijacking”. This result by itself invalidates the classical timescale separation hypothesis: we see here that increased millennial variability causes the ice age cycles to fade.
- c.
Millennial forcings can be aggregated: Several sinusoids of smaller amplitudes and of different millennial periods create the same hijacking effect as a single 5 kyr high-amplitude sinusoid, moving the system into the phase-plane domain of higher temperatures and lower ice volume (Fig. 1c).
- d.
Acting alone, low-amplitude millennial sinusoids preserve their original frequencies. However, several components may generate low-frequency beatings, which are then demodulated by the system. Through this mechanism, millennial forcing may induce responses at periods close to the orbital periods, e.g., periods of precession and obliquity (Fig. 1d). For example, the 41 kyr mode in Fig. 1d, which one might be tempted to attribute to obliquity, is in fact the demodulation of the envelope generated by the interplay of the 6 and 7 kyr forcing sinusoids: –1∕7.
It is possible to anticipate the disruptive effect of forcing at other periods. Indeed, let us measure this disruption potential as the distance ΔS (km2) on the phase plane between the system's equilibrium point with zero forcing and the time mean ice sheet area expected given a periodic forcing of amplitude ε and period T (Fig. 1a, c). In Verbitsky et al. (2018), we have shown that the dynamical properties of the system are largely determined by the V number. We therefore may expect . Since V is dimensionless and since the dimensions of ε (km kyr−1) and T (kyr) are independent (in our model, the forcing is introduced as a component of ice sheet mass balance and therefore ε has the same dimension as ice ablation rate; km kyr−1), the π theorem (Buckingham, 1914) tells us that . We determined experimentally that ΔS=0 if V=0 and that Φ(V) can be approximated as a linear function. The scaling argument finally brings us to
where is the frequency, and μ is a constant that has to be determined experimentally. We thus see that . The −2 frequency slope of ΔS has been confirmed in additional numerical experiments (not shown here) for forcing periods between 2 and 20 kyr. The 5 kyr period sinusoids and multiple sinusoids of periods spread between 3 and 9 kyr are arbitrary choices used to illustrate the hijacking and beating effects. The phenomena can be replicated with other modes of millennial activity such as, for example, 6.5, 2.5, 0.9, and 0.5 kyr periods identified by Dima and Lohmann (2009). For example, we confirmed that, as it is implied by Eq. (1), the hijacking effect of a 6.5 kyr sinusoid is the same as that of a 5 kyr sinusoid if the ratio of the corresponding amplitudes is 0.77.
Similar scaling arguments can be applied to the amplitude of the S variable, i.e., the amplitude of the glacial area over a glacial cycle. This amplitude has the same dimension as ΔS; i.e., and , where T is the period of the system response. Depending on the value of the V number, the system response may feature periods of external forcing or multiples of forcing periods or combinations of these. Accordingly, Fig. 1d shows a −1.9 slope in the orbital frequency domain (though, again, all peaks in this domain are, in fact, created by the millennial forcing) and a −2 slope for the millennial domain. We regard this result as a remarkable test in favor of the above hypothesis; i.e., . Different aspects of glacial geometry such as area (S), ice thickness (; Verbitsky, et al., 2018), glaciation horizontal span (, or ice volume ( may play a role in shaping climate conditions at a specific geographical point. Thus, corresponding power spectra of empirical records may have frequency slopes ranging from −5 () to −1 ().
For multi-period forcing in a frequency domain Δf, the aggregate hijacking potential ΔSA can be estimated as
Accordingly, since amplitudes of high-frequency variability, ε(f), may compensate for the frequency damping (f−2), centennial, decennial, and perhaps even annual variations potentially may contaminate the spectrum throughout the millennial and multi-millennial range and perturb ice age dynamics via two physical mechanisms: (a) centennial and millennial oscillations shift the mean state of the system, and (b) the sensitivity of ice sheets to the astronomical forcing depends on the system state.
To our knowledge, only Le Treut and Ghil (1983) have previously adopted a deterministic framework to model a background spectrum connecting millennial to astronomical timescales. Unfortunately, their model did not generate credible ice age time series. The more common route for simulating the centennial and millennial spectrum is to introduce a stochastic forcing (e.g., Wunsch, 2003; Ditlevsen and Crucifix, 2017). Such stochastic forcing may in principle be justified by the existence of chaotic or turbulent motion in the atmosphere–ocean continuum. However, whether such forcing is large enough to integrate all the way up to timescales of several tens of thousands of years is speculative. The deterministic theory proposed here presents the advantage of using the nonlinear character of ice sheet dynamics, which was derived naturally from the conservation laws and therefore provides a clear physical interpretation of the nonlinear origin of the cascade. Our approach is thus remarkably parsimonious because it requires no more physics than the minimum needed to explain ice ages plus the existence of centennial or millennium modes of motions. The latter may very plausibly arise as modes of ocean motion (Dijkstra and Ghil, 2005; Peltier and Vettoretti, 2014). Of course, stochastic forcing may still be added, and its cumulated effects would then be estimated by Eq. (2).
In summary, using a deterministic nonlinear dynamical model of the global climate, we demonstrated that astronomical timescale variability cannot be considered separately from millennial phenomena and that the ice dynamics are an effective vehicle for propagating high-frequency forcing into the orbital timescale. This may imply that the knowledge of millennial and centennial variability is needed to fully understand and replicate ice age history. As we have seen, increased millennial variability decreases the length of the ice age cycles. However, the reverse is also true. This state of affairs generates a new hypothesis for the middle Pleistocene transition: a decrease in millennial variability may have caused the lengthening of ice ages. The millennial variability can legitimately be modeled as a deterministic mode, which would allow us to come up with a specific explanation of how this variability may influence ice age dynamics. Hence our completely deterministic approach makes a physically justified alternative to a popular notion that the background spectrum is merely linearly integrated noise.
The MatLab R2015b code and data to calculate the model response to astronomical and millennial forcing (Verbitsky et al., 2019) are available at https://doi.org/10.5281/zenodo.2628310 (last access: 4 April 2019).
MYV conceived the research and developed the model. MYV and MC wrote the paper. DMV developed the numerical scheme and MatLab code.
The authors declare that they have no conflict of interest.
Michel Crucifix is funded by the Belgian National Fund of Scientific Research. Dmitry M. Volobuev is funded in part by the Russian Foundation for Basic Research, grant 19-02-00088-a. We are grateful to our reviewers Gerrit Lohmann and Niklas Boers for their helpful comments.
This paper was edited by Anders Levermann and reviewed by Gerrit Lohmann and Niklas Boers.
Berger, A. and Loutre, M. F.: Insolation values for the climate of the last 10 million years, Quaternary Sci. Rev., 10, 297–317, 1991.
Buckingham, E.: On physically similar systems; illustrations of the use of dimensional equations, Phys. Rev., 4, 345–376, 1914.
Dijkstra, H. A. and Ghil, M.: Low-frequency variability of the large-scale ocean circulation: A dynamical systems approach, Rev. Geophys., 43, RG3002, https://doi.org/10.1029/2002RG000122, 2005.
Ditlevsen, P. and Crucifix, M.: On the importance of centennial variability for ice ages, Past Global Changes Magazine, 25, 152–153, 2017.
Dima, M. and Lohmann, G.: Conceptual model for millennial climate variability: a possible combined solar-thermohaline circulation origin for the ∼ 1,500-year cycle, Clim. Dynam., 32, 301–311, 2009.
Huybers, P. and Curry, W.: Links between annual, Milankovitch and continuum temperature variability, Nature, 441, 329–332, https://doi.org/10.1038/nature04745, 2006.
Le Treut, H. and Ghil, M.: Orbital forcing, climatic interactions and glaciation cycles, J. Geophys. Res., 88, 5167–5190, https://doi.org/10.1029/JC088iC09p05167, 1983.
Omta, A. W., Kooi, B. W., Voorn, G. A. K., Rickaby, R. E. M., and Follows, M. J.: Inherent characteristics of sawtooth cycles can explain different glacial periodicities, Clim. Dynam., 46, 557–569, https://doi.org/10.1007/s00382-015-2598-x, 2016.
Peltier, R. W. and Vettoretti, G.: Dansgaard-Oeschger oscillations predicted in a comprehensive model of glacial climate: A “kicked” salt oscillator in the Atlantic, Geophys. Res. Lett., 41, 7306–7313, https://doi.org/10.1002/2014GL061413, 2014.
Saltzman, B.: Three basic problems of paleoclimatic modeling: A personal perspective and review, Clim. Dynam., 5, 67–78, 1990.
Saltzman, B. and Verbitsky, M. Y.: Multiple instabilities and modes of glacial rhythmicity in the Plio-Pleistocene: a general theory of late Cenozoic climatic change, Clim. Dynam., 9, 1–15, 1993.
Verbitsky, M. Y., Crucifix, M., and Volobuev, D. M.: A theory of Pleistocene glacial rhythmicity, Earth Syst. Dynam., 9, 1025–1043, https://doi.org/10.5194/esd-9-1025-2018, 2018.
Verbitsky, M. Y., Crucifix, M., and Volobuev, D. M.: Supplementary code and data to paper “ESD Ideas: Propagation of high-frequency forcing to ice age dynamics” (Version 1.0), Zenodo, available at: https://doi.org/10.5281/zenodo.2628310, last access: 4 April 2019.
Wunsch, C.: The spectral description of climate change including the 100 ky energy, Clim. Dynam., 20, 353–363, 2003.





