the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
On the assessment of the moisture transport by the Great Plains low-level jet
Jorge Eiras-Barca
Gonzalo Miguez-Macho
Raquel Nieto
Luis Gimeno
Low-level jets (LLJs) can be defined as wind corridors of anomalously high wind speed values located within the first kilometre of the troposphere. These structures are one of the major meteorological systems in the meridional transport of moisture on a global scale. In this work, we focus on the southerly Great Plains low-level jet, which plays an important role in the moisture transport balance over the central United States. The Gulf of Mexico is the main moisture source for the Great Plains low-level jet (GPLLJ), which has been identified as a key factor for rainfall modulation over the eastern and central US.
The relationship between moisture transport from the Gulf of Mexico to the Great Plains and precipitation has been well documented in previous studies. Nevertheless, a large uncertainty still remains in the quantification of the moisture amount actually carried by the GPLLJ. The main goal of this work is to address this question. For this purpose, a relatively new tool, the regional atmospheric Weather Research and Forecasting Model with 3-D water vapour tracers (WRF-WVT; Insua-Costa and Miguez-Macho, 2018) is used together with the Lagrangian model FLEXPART to estimate the load of precipitable water advected within the GPLLJ. Both models were fed with data from ERA Interim. From a climatology of jet intensity over a 37-year period, which follows a Gaussian distribution, we select five cases for study, representing the mean and 1 and 2 standard deviations above and below it. Results show that the jet is responsible for roughly 70 %–80 % of the moisture transport occurring in the southern Great Plains when a jet event occurs. Furthermore, moisture transport by the GPLLJ extends to the north-east US, accounting for 50 % of the total in areas near the Great Lakes. Vertical distributions show the maximum of moisture advected by the GPLLJ at surface levels and maximum values of moisture flux about 500 m above, in coincidence with the wind speed profile.
- Article
(5796 KB) -
Supplement
(4231 KB) - BibTeX
- EndNote
It is well known that the Great Plains low-level jet (hereafter, GPLLJ) plays an important role in the balance of the moisture transport over the central United States (Stensrud, 1996; Schubert et al., 1998). The atmospheric moisture is transported by the GPLLJ from tropical and subtropical latitudes (particularly the Gulf of Mexico and the Caribbean Sea) into the Great Plains (Helfand and Schubert, 1995; Mo et al., 1997), where the jet is often responsible for nocturnal deep convective activity (Higgins et al., 1997; Pu et al., 2016). In the last decades, a large number of authors have shown the strong influence of the GPLLJ as a modulator of climate and rainfall over this region and even further east (Mo et al., 1995, 1997; Wu and Raman, 1998; Byerle and Paegle, 2003); for instance, throughout May and June it is estimated that at least one-third of the moisture penetrating into the continental US is carried by the GPLLJ (Helfand and Schubert, 1995).
Among the mechanisms which have been proposed as triggers of the GPLLJ are included a combination of inertial oscillations (Blackadar, 1957) and orographic forcing (Wexler, 1961; Byerle and Paegle, 2003; Pan et al., 2004; Ting and Wang, 2006). In particular, the mechanism of Blackadar (1957) suggests that inertial oscillations near the friction layer can induce the formation of the GPLLJ (Wu and Raman, 1998). Nevertheless, orographic effects are also understood as a key factor in the maintenance of the GPLLJ. In this regard, Ting and Wang (2006) proved that, when the interaction with the orography is removed from numerical simulations, the GPLLJ vanishes, together with an important amount of the summer precipitation over the central and southerly US.
The GPLLJ is a phenomenon confined within the first kilometres of the troposphere and is closely related to the warm season (Bonner, 1968). Moreover, it is characterised by a strong diurnal oscillation, with a peak in strength during night hours (Augustine and Caracena, 1994). A long-term climatology of GPLLJ can be found in the work of Walters et al. (2008). The GPLLJ is a phenomenon extremely localised in time and space, and its role in the continental moisture balance is difficult to study solely from observations.
Nevertheless, a large number of studies have documented the relationship between the major moisture transport and the GPLLJ. Higgins et al. (1996) studied the moisture budget over the central US in May employing NASA/DAO and NCEP/NCAR datasets, together with station observations, to evaluate the limitations of these products. Although both reanalyses overestimate daily mean precipitation rates, they accurately capture the basic temporal and structural characteristics of the GPLLJ. From the data, these authors calculated an increase in atmospheric moisture transport from the Gulf of Mexico during night-time of more than 50 %. In a later work, Higgins et al. (1997) observed a well-defined nocturnal maximum of precipitation over the Great Plains in spring and summer by analysing station data. Linked to low-level jet (LLJ) events, they particularly found an excess of 25 % in the region in nocturnal rainfall during summer when compared with the diurnal precipitation, associated with a rainfall decrease over the Gulf of Mexico. Additionally, Higgins et al. (1997) reported significant differences in precipitation pattern in coincidence (or not) with LLJ events. When an LLJ event occurs, the observations show an enhanced precipitation over the north-central United States and the Great Plains region, together with a decrease along the Gulf of Mexico and the western Atlantic. On the other hand, Mo and Juang (2003) found regional correlation at a distance between evaporation and precipitation, reflected in evaporation anomalies over the Great Plains along the trajectory of the GPLLJ, which are associated with downstream precipitation anomalies.
Otherwise, extreme rainfall events in the central US are related to an increase in moisture convergence downwind of the GPLLJ (Mo et al., 1997). A decisive factor that triggers heavy rains and floods is the presence of moisture advected by the GPLLJ from the Gulf of Mexico and the Caribbean Sea. Moore et al. (2012) reported the physical processes related to the floods in May 2010, when a persistent southerly LLJ associated with an atmospheric river (AR) enhanced the transport of moisture from the Gulf of Mexico into the heavy rainfall region. Thus, important socioeconomic impacts follow enhanced GPLLJ events, which modulates a large percentage of the local extreme precipitation events and flooding in warmer months (Mo et al., 1995, 1997; Beljaars et al., 1996; Trenberth and Guillemot, 1996; Arritt et al., 1997; Nakamura et al., 2013; Nayak et al., 2016). All these results are consistent with the large-scale atmospheric moisture transport and support the marked influence of the GPLLJ over the central-eastern US, which has been shown to trigger more than 60 % of the spring local precipitation over the Great Plains region (Wang and Chen, 2009).
During the last decades, the GPLLJ has experienced a strengthening, accompanied by a northward migration causing a displacement of rainfall in the same direction. As a result, more frequent droughts have been observed in the southern Great Plains (Barandiaran et al., 2013). Moreover, an increase in the number and intensity of GPLLJ events is also forecasted for future projections, which reveal an intensification of the GPLLJ during the spring season associated with global warming (Cook et al., 2008; Tang et al., 2017). As a result, increasing amounts of moisture transport and rainfall are expected, particularly from April to July, over the central US (Harding and Snyder, 2014). The same projections forecast a slight weakening of the GPLLJ from August to December, which could translate into increasing drought conditions.
The knowledge about the GPLLJ, together with the insights on the relationship between the moisture transported by the GPLLJ and local precipitation patterns, has increased considerably during the last decades. However, there are still unanswered questions about the quantification of such water vapour transport and especially about the estimation of the ratio of land to oceanic moisture sources associated with the GPLLJ. This estimate of the oceanic input to the moisture transport associated with the GPLLJ is essential to predict and understand the behaviour of the GPLLJ in future scenarios.
In this work, a new tool, the regional atmospheric Weather Research and Forecasting Model with 3-D water vapour tracer diagnostics (WRF-WVT, Insua-Costa and Miguez-Macho, 2017), is used to quantify the total amount of total precipitable water (TPW) transported by the GPLLJ. To show the differences between the transport of moisture on jet and non-jet days, a 37-year climatology of maximum jet intensity is obtained following the methodology of Rife et al. (2010). The structure of this work is as follows: in Sect. 2 we provide the methodology used, in Sect. 3 we show the results obtained, and finally in Sect. 4 we discuss the conclusions.
2.1 Detection of the Great Plains low-level jet
To objectively detect days with LLJ over the Great Plains, we applied the night-time index proposed in Rife et al. (2010), hereafter named NLLJ. This index is based on the temporal variation in the wind's vertical structure and the fact that LLJs are most intense at local midnight. Because both the frequency and intensity of GPLLJ are mostly associated with the warm season, we develop a 37-year climatology for the month of July (representative of the boreal summer). According to the NLLJs characteristics, and with the aim to define the index, two conditions should be met to consider a GPLLJ detection:
-
The wind speed is higher at local midnight than at midday.
-
The local midnight wind speed is higher at the surface (∼500 m) than above it (∼4 km).
The index is calculated at each grid point over an area centred over the US using 6-hourly ERA-Interim reanalysis data (Dee et al., 2011) with a 0.25∘ horizontal resolution. Because the jet core is located within of the first kilometre of the troposphere, it is necessary to take into account the elevation of the land, so sigma coordinates are used. The GPLLJ-climatology is developed for 37 years, from 1980 to 2016, and the NLLJ index can be defined as follows:
where u and v are the zonal and meridional wind components, respectively. L1 represents the winds at the surface at the 53 sigma level (elevation near the jet core), approximately 500 m above ground level (a.g.l.), while L2 corresponds to the wind at the 42 sigma level (around 4000 m a.g.l.). Numbers 00 and 12 refer to local midnight and local noon, respectively. λ and φ are binary multipliers representing the temporal and vertical variation in the wind. In particular, λ relates to the daily variation in the wind at 500 m, and φ refers to the wind's vertical variation between 500 m and 4 km at midnight (Rife et al., 2010):
2.2 Identification of moisture sources associated with the Great Plains low-level jet
For the objective identification of moisture sources associated with the GPLLJ, the Lagrangian backward trajectories from the FLEXPART v9.0 model are used (Stohl et al., 2005a). This model provides a large number of air parcel trajectories from which it is possible to calculate the evaporation minus precipitation budget, tracking all changes in the specific humidity of air parcels.
FLEXPART has been widely and successfully used to track moisture paths for the study of the atmospheric branch of the hydrologic cycle in different parts of the world (e.g. Vázquez et al., 2016; Hu et al., 2018; Sorí et al., 2018). Furthermore, this tool is able to infer the moisture sources for precipitation falling in a target region when backward trajectories are considered (e.g. Stohl et al., 2008; Drumond et al., 2010; Gimeno et al., 2012; Wegmann et al., 2015; Ramos et al., 2016).
In this work we use the outputs of a global experiment in which FLEXPART v9.0 tracks approximately 2 million particles (air parcels) with constant mass distributed on the globe every time step during a 37-year period (1980–2016). These air parcels are advected by the 3-D wind field, and the variables of interest of each particle (position, height, specific humidity and temperature among many others) are saved at each time step. We perform a FLEXPART simulation fed with ERA-Interim reanalysis data at a horizontal resolution on 61 vertical levels from sea level hPa and 6 h time intervals (00:00, 06:00, 12:00 and 18:00 UTC). The model is run with a 3 h time step, and linear interpolation is used to obtain data with this frequency from ERA-Interim. The backward trajectories are followed for 10 days, which is the average lifetime of water vapour in the atmosphere (Numaguti, 1999).
The changes in specific humidity (q) of each air parcel along its path can be expressed as follows:
where m is the mass of a particle (which remains constant in the simulation), q is the specific humidity, t the time step and e−p (evaporation minus precipitation) represents the water flux associated with the particle. To obtain the instantaneous values of the E−P balance (E denotes evaporation and P the precipitation rate per unit area) in a given area (in this case, over one of in latitude and longitude), it is necessary to integrate the moisture changes for all particles present in the atmospheric column over such an area (Stohl and James, 2004, 2005b). Thus, following this methodology, in a backward experiment, a moisture source is defined as those regions where E−P is positive , which implies that evaporation exceeds precipitation, while a moisture sink is defined as a region where (, meaning that precipitation is greater than evaporation.
In our study, backward trajectories were followed from the area composed of points with values of the NLLJ above the 75th percentile to find the main moisture source.
2.3 The regional atmospheric Weather Research and Forecasting Model with 3-D water vapour tracer diagnostics
The mesoscale WRF-WVT (Miguez-Macho et al., 2013; Insua-Costa and Miguez-Macho, 2018) is used to quantify the amount of total precipitable water (TPW) transported by the GPLLJ. In order to analyse the moisture transport associated with the GPLLJ avoiding the effects of other synoptic-scale transport events, we tag the moisture passing northward through a narrow wall located on the northern edge of the moisture source region identified using the FLEXPART model. When a particle of water (whether in liquid, solid or gas state) crosses the wall, it is labelled for further analysis inside the simulation domain. We consider all water traversing the wall to be advected by the GPLLJ.
The horizontal resolution of the simulations is 20 km, and the vertical column is divided into 38 levels. The simulation covers a time window of 11 days, starting 7 days prior to the day of interest. The model parameterisations together with the WRF-WVT are set using the planetary boundary layer (PBL) Yonssei University (YSU) parameterisation (Hu et al., 2013; Shin and Hong, 2011), the Kain–Fritsch schemes for convection (Kain, 2004), the Dudhia one for short-wave radiation (Dudhia, 1989), the Rapid Radiative Transfer Model (RRTM) scheme for long-wave radiation (Mlawer et al., 1997), and the WRF Single-Moment 6-Class Microphysics Scheme (WSM6) (Hong and Lim, 2006).
In addition, we apply spectral nudging of waves longer than 1000 km above the boundary layer, with a relaxation time of 1 h, to avoid the distortion of the large-scale circulation. This configuration has been validated and successfully applied several times with the WRF-WVT in midlatitudes (e.g. Eiras-Barca et al., 2017). Spectral nudging ensures that the large-scale circulation is well captured in the simulations. ERA-Interim data provide lateral boundary and initial conditions for the runs (Dee et al., 2011). The variables of interest for the analysis of the GPLLJ event are computed as follows. Integrated water vapour (IWV), Eq. (5) is obtained by vertical integration of the specific humidity (q) in pressure (p) levels, where g represents the gravitational force. The instant flux of moisture (σ) is calculated as stated in Eq. (6), and the conversion between g and the water vapour mixing ratio obtained from WRF is performed using Eq. (7), where u and v are the horizontal components of the wind field.
3.1 Characterisation of the Great Plains low-level jet
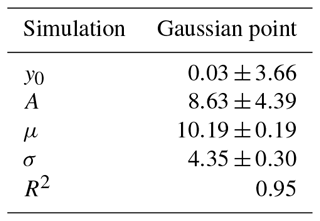
As previously mentioned, the NLLJ index was calculated at each grid point over the North American region for the month of July over the period 1980–2016. July was found to be the month with maximum LLJ events (Fig. S1 in the Supplement shows the monthly distribution of the GPLLJ days of detection). Figure 1a shows the climatological NLLJ index and the wind field at 500 hPa. The black cross indicates the point of maximum intensity of the index (8.8 m s−1). At this point, located at 32.75∘ N, 99∘ W, along the 37-year analysed and for July a total of 931 LLJ days are identified; that is, 81 % of all days have a positive value of the index. At the point of maximum intensity shown in Fig. 1a, Fig. 1b displays the frequency distribution of the NLLJ for the period 1980–2016. A clear peak around 11 m s−1 is observed together with Gaussian behaviour (Jarque–Bera test p value = 0.0055, which provides a confidence level close to 99.5 %; red line). The latter has been used to select the five case studies to be analysed with WRF-WVT and listed in Table 1. The five case studies were selected based on the Gaussian adjustment applied to the study. These five events correspond to μ, μ±2σ and μ±σ (where μ is the mean of the distribution and σ its standard deviation), and they provide a general perspective of the LLJ's behaviour. Selecting these case studies from the population of LLJ events decreases the computational expense. Since each case study WRF-WVT simulation spans 11 days, a condition of persistence of the index value for at least 2 days after the main jet day is applied. Additionally, we perform a sixth simulation with a non-jet day (simulation 0 in the Table 1). This non-jet day is selected from the developed climatology as the longest non-jet period, in order to avoid overlaps in moisture transport with jet days.
Table 1Case studies objectively selected based on the frequency distribution of the NLLJ index to carry out WRF-WVT simulations. μ is the mean of the distribution and σ its standard deviation. Note: the frequency distribution is calculated at the point of maximum intensity of the NLLJ at 32.75∘ N, 99∘ W (black cross in Fig. 1a) using the ERA-Interim reanalysis dataset.
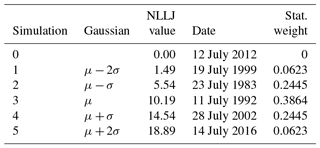
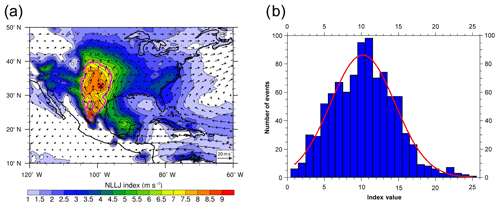
Figure 1(a) Mean NLLJ index (shaded) and 500 m winds (arrows, in m s−1) at local midnight in July (boreal summer) for 1980–2016, calculated from ERA-Interim reanalysis. The black cross at 32.75∘ N, 99∘ W shows the point of maximum NLLJ in the climatology. The magenta contour line surrounds the region containing points above the 75th percentile. (b) Frequency distributions of the GPLLJ for the months of July from 1980 to 2016 (blue bars). The red curve corresponds to the Gaussian fit (see Table A2). Note: the frequency distributions are calculated at the point of maximum intensity of the NLLJ (at 32.75∘ N, 99∘ W; black cross in a).
3.2 Moisture transport associated with the Great Plains low-level jet
In order to detect the main climatological oceanic source of moisture for the GPLLJ, we used the FLEXPART trajectories outputs for 1980–2016. The area encompassed in the 75th percentile of the NLLJ index values (magenta line in Fig. 1a) was selected as the target region for the backward experiment (as explained in the methodology). Figure 2 shows the source of moisture in red colour, obtained as the 75th percentile of the () field. This area covers the southern Gulf of Mexico and extends into the Caribbean Sea, between 60–98∘ W and 12–28∘ N. Figure S2 in the Supplement shows the individual sources of moisture for each case in study.
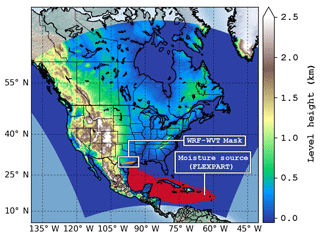
Figure 2Highlighted in red are moisture sources obtained with FLEXPART from backward trajectories originating in the region outlined in magenta in Fig. 1a. The orange line over the continent marks the position from where precipitable water is tagged in WRF-WVT, corresponding to the northern edge of the FLEXPART source region. All water vapour and condensate crossing through that line is considered as moisture advected by the GPLLJ for further analysis.
Although the flow originating in the source of moisture is advected at low levels as a result of the strong intensity of the trade winds, a 3-D-label wall (at 29–30∘ N and from 94.5 to 100∘ W) was used in the WRF-WVT simulations (orange line in Fig. 2). The position of the sentinel wall was selected in the region where oceanic moisture associated with the GPLLJ makes landfall. The wall remained constant in the WRF-WVT simulations. The thin wall was used instead of the entire source regions in order to avoid overlaps in the labelling of moisture caused by secondary, synoptic-scale mechanisms.
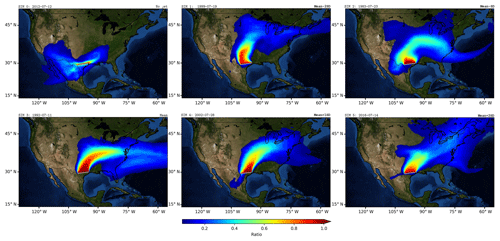
Figure 3Ratio of tagged precipitable water transported by the GPLLJ to total for the six case studies analysed.
Figure 3 shows the ratio of precipitable water transported by the GPLLJ to total precipitable water (TPWtracers=TPW) for the six case studies analysed. As mentioned earlier, TPWtracers represents the TPW that has crossed the “wall” highlighted in orange in Fig. 2, which we assume corresponds to moisture advected by the GPLLJ. Following the same behaviour of the GPLLJ itself, the moisture flux is initially in the northward direction and veers east as it penetrates into the Great Plains for all events with positive NLLJ index values. As expected, the non-jet event with an NLLJ value equal to zero (Sim 0) does not show significant moisture fluxes. For the jet events, ratios are close to 1 in regions near the tagging wall and extend for hundreds of kilometres northward, with significant values above 60 %. Percentages between 70 % and 80 % are observed in the Great Plains. The large geographical reach of the moisture associated with the GPLLJ is evidenced in this figure, showing that for certain GPLLJ events, it can occasionally explain more than 50 % of TPW even in the north-east US. It is necessary to highlight that higher values in the index do not necessarily mean larger flows of moisture, as can be observed, for example, when Sim 3 and Sim 5 are compared. Figure S3 in the Supplement shows a comparison of accumulated precipitation at 11 days of WRF simulations versus Climate Prediction Center (CPC) gauge-analysis observations (Chen et al., 2008).
As previously stated, the aim of this work is to study the general behaviour of the GPLLJ associated with its moisture transport. In the first simulated case of GPLLJ (Fig. 3 – Sim 1) it is observed that most of the precipitable water is concentrated on the Great Plains, exceeding ratios of 80 % out of the total. In the second GPLLJ event simulated (Fig. 3 – Sim 2), the precipitable water extends north-east of the US and to the south of the Great Lakes and the GPLLJ, where it explains close to the 50 % of precipitable water. The third simulated case corresponds to the average behaviour of the GPLLJ (Fig. 3 – Sim 3) and shows the influence of the GPLLJ in the north-east of the US with ratios near 50 % on the US east coast. Nevertheless, in areas along the path of the GPLLJ, the advection of precipitable water is close to 80 %. In the fourth and fifth simulations of GPLLJ (Fig. 3 – Sim 4 and 5), the plume of precipitable water is concentrated over the Great Plains. However, the water precipitable ratio is reduced as latitude increases, but values are still close to 50 % in the north-eastern areas of the US.
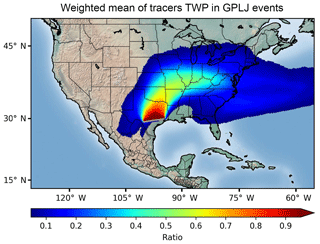
Figure 4Statistically weighted ratio of precipitable water transported by the GPLLJ for the five case studies with NLLJ > 0 considered in the analysis in Fig. 3. Weights applied are stated in Table 1.
Figure 4 shows the statistically weighted mean of the ratio shown in Fig. 3 for the five case studies with NLLJ>0 considered in the analysis. The weights associated with each event are stated in the last column of Table 1, and the objective criteria to assign them can be found in Appendix A1. The aim of using weights in the analysis is to give greater importance to the event representing the mean value of the NLLJ and less relevance to the events in the tail of the distribution. Notwithstanding the limited number of simulations used in the analysis, this procedure allows us to interpret Fig. 4 as a “climatology” of the moisture transport associated with the GPLLJ. Roughly 80 %–90 % of the precipitable water in its core zone of influence over the Great Plains, in Texas and Oklahoma, is carried by the GPLLJ when a jet event occurs. With increased distance from that area, the ratio of precipitable water transported by the GPLLJ decreases; however, the contribution of moisture from the Gulf of Mexico to TPW is still more than 50 % as far north as the Great Lakes.
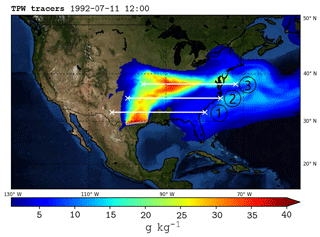
Figure 5Tracer total precipitable water (TPW, g kg−1) and positions of the cross sections along the central axis of the GPLLJ shown in Figs. 6 and 7, at latitudes 32∘ N (1), 35∘ N (2) and 38∘ N (3) for the main jet event of 11 July 1992.
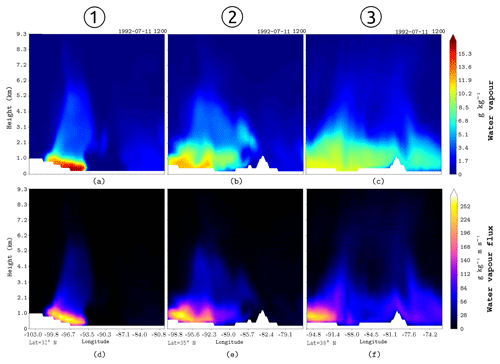
Figure 6(a–c) qTR in g kg−1 for the three vertical cross sections at the locations depicted by white lines in Fig. 5. Panels (d–f) same as (a–c) but for φTR in g m (kg s)−1.
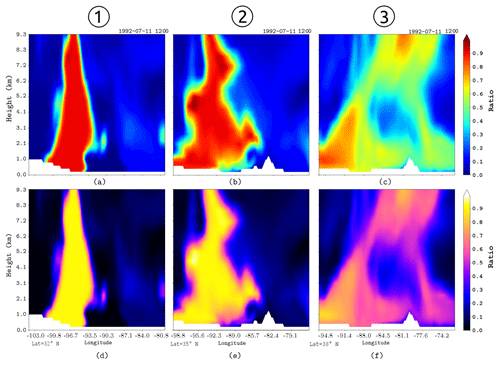
Figure 7(a–c) Ratio of qTR:q for the three vertical cross sections at the locations depicted by white lines in Fig. 5. Panels (d–f) same as (a–c) but for a ratio of phiTR:phi.
Figure 5 shows the TPW and the cross sections for the main GPLLJ event (11 July 1992). Figure 6 shows the vertical distribution of tracer-specific humidity (qTR) and tracer water vapour flux (φTR) for cross sections at positions depicted in Fig. 5. Tracer moisture (Fig. 6a–c) has a maximum at surface levels, while the moisture flux (Fig. 6d–f) maximises at 500 m a.g.l. where the LLJ core is located. A significant presence of both tracer water vapour and tracer water vapour flux is restricted to the first 2 km a.g.l. Overall, as the latitude increases the water vapour plume from the Gulf of Mexico tends to rise in the vertical column and expand zonally along the GPLLJ path to the east of the US. Equivalent conclusions can be obtained from the remaining events, which are shown in the Supplement (Figs. S4–S7 in the Supplement). Figure 7 shows the water vapour ratio qTR:q for the vertical sections of Fig. 5 for the same event. The moisture pattern behaviour is similar to Fig. 6; for regions close to the Gulf of Mexico the moisture ratio is concentrated mostly at lower levels (Fig. 7a) and extends on the horizontal axis as it moves away from the source of moisture (Fig. 7b). Nevertheless, for remote regions the maximum moisture ratio continues at lower levels (Fig. 7c). The moisture flow has the same pattern: high moisture ratios that remain at low levels despite longitudinal distance (Fig. 7d–f). These results confirm that the GPLLJ transports a great concentrated quantity of moisture.
A combination of Lagrangian and Eulerian methods was used to identify and objectively quantify the moisture transport associated with the GPLLJ. First, the FLEXPART Langrangian model was used to locate the GPLLJ moisture sources for the month of its maximum activity (July) throughout the period 1980–2016. The target region used in the FLEXPART simulation to find the main source of moisture was defined based on the 75th percentile of the GPLLJ index value previously calculated based on the Rife et al. (2010) method. Once the Gulf of Mexico was identified as the main source of moisture () for the GPLLJ, we use a new tool known as Eulerian 3-D WRF-WVT (Insua-Costa and Miguez-Macho, 2018), which was applied to track the moisture advected in six selected GPLLJ events based on the distribution of the GPLLJ index used previously to detect the GPLLJ (Rife et al., 2010). Consequently, this work analysed the behaviour of the GPLLJ during the month of its maximum activity (July) for the period 1980–2016, and we select six representative cases for the WRF-WVT simulation.
The moisture transport analysis reveals the major role played by the GPLLJ in the water cycle of central North America, transporting large amounts of moisture from the Gulf of Mexico as far as the north-east US. In particular, advection by the jet explains more than 80 % of the precipitable water in the southern Great Plains when a jet event occurs, which, in July, is most of the days. The Rocky Mountains block the circulation of GPLLJ and force it to turn to the east of the US, reaching even the eastern coast of the US. The moisture transport associated with the GPLLJ is in a plume of moisture, where the maximum transport occurs in the path of the GPLLJ. As expected, the ratio reduces as latitude increases, but values are still close to 50 % in the north-eastern areas of the US.
We note that the extension of the GPLLJ is dependent on the synoptic conditions or land preconditioning, among other factors, which may alter the ratio of the TPW. For example, the presence of a well-developed high-pressure system at higher latitudes of North America may block the advection of the GPLLJ moisture to this region. Dong et al. (2011) related the drought of 2006 with an anomalous high over the south-western US region and an anomalous low over the Great Lakes. This pattern inhibited the advection of moisture from the Gulf of Mexico, contributing to the extreme dryness, and the lack precipitation was associated with a suppressed cyclonic activity over the south-western US. On the other hand, the 2007 flood events were initially preceded by active synoptic weather patterns, linked to an active moisture transport from the Gulf of Mexico by the GPLLJ. Nevertheless, the analysis of these multiple factors is beyond the scope of this paper.
Higher values in the NLLJ index mean larger differences between winds aloft and at the surface at the reference point, but they do not necessarily mean stronger moisture transport.
These results should be understood as a first approach to the quantification of the large extent of GPLLJ moisture advection and its implications for the water budget in North America. More simulations should be conducted, and other months should be included in FLEXPART backward calculations to extend this work and produce a more comprehensive analysis.
No public data are derived from this research. For further information on the WRF-WVT tool, please contact the corresponding author.
The supplement related to this article is available online at: https://doi.org/10.5194/esd-10-107-2019-supplement.
IA, RN and LG had the initial idea. GMM developed the WRF-WVT tool. IA and JEB carried out the simulations and data analysis. IA and JEB wrote the original draft and reviewed the subsequent documents. RN, LG and GMM provided suggestions during the revision period.
The authors declare that they have no conflict of interest.
This article is part of the special issue “The 8th EGU Leonardo Conference: From evaporation to precipitation: the atmospheric moisture transport”. It is a result of the 8th EGU Leonardo Conference, Ourense, Spain, 25–27 October 2016.
Iago Algarra was financially supported by the Spanish government (MINECO,
CGL2015-65141-R). Jorge Eiras-Barca was financially supported by the EDB481B
2018/069 from the Xunta de Galicia and the Fulbright Commission. This work
was also partially supported by Xunta de Galicia under Project ED431C
2017/64-GRC “Programa de Consolidación e Estructuración de Unidades
de Investigación Competitivas (Grupos de Referencia Competitiva)”. This
work is part of the LAGRIMA project. The computational part of this work was
done in the Supercomputing Center of Galicia, CESGA. Iago Algarra would like
to express his gratitude to all the Non-Linear Physics Group for their kind
support during his stay at the University of Santiago de Compostela. Finally
the authors would like to thank two anonymous referees, who helped to improve
the final version of the manuscript.
Edited by:
Francina Domínguez
Reviewed by: two anonymous referees
Arritt, R. W., Rink, T. D., Segal, M., Todey, D. P., Clark, C. A., Mitchell, M. J., Labas, K. M., Arritt, R. W., Rink, T. D., Segal, M., Todey, D. P., Clark, C. A., Mitchell, M. J., and Labas, K. M.: The Great Plains Low-Level Jet during the Warm Season of 1993, Mon. Weather Rev., 125, 2176–2192, https://doi.org/10.1175/1520-0493(1997)125<2176:TGPLLJ>2.0.CO;2, 1997.
Augustine, J. A. and Caracena, F.: Lower-tropospheric precursors to nocturnal MCS development over the central United States, Weather Forecast., 9, 116–135, https://doi.org/10.1175/1520-0434(1994)009<0116:LTPTNM>2.0.CO;2, 1994.
Barandiaran, D., Wang, S.-Y., and Hilburn, K.: Observed trends in the Great Plains low-level jet and associated precipitation changes in relation to recent droughts, Geophys. Res. Lett., 40, 6247–6251, https://doi.org/10.1002/2013GL058296, 2013.
Beljaars, A. C. M., Viterbo, P., Miller, M. J., and Betts, A. K.: The Anomalous Rainfall over the United States during July 1993: Sensitivity to Land Surface Parameterization and Soil Moisture Anomalies, Mon. Weather Rev., 124, 362–383, https://doi.org/10.1175/1520-0493(1996)124<0362:TAROTU>2.0.CO;2, 1996.
Blackadar, A. K.: Boundary layer wind maxima and their significance for the growth of nocturnal inversions, B. Am. Meteorol. Soc., 38, 283–290, https://doi.org/10.1175/1520-0477-38.5.283, 1957.
Bonner, W. D.: Climatology of the low level jet, Mon. Weather Rev., 96, 833–850, https://doi.org/10.1175/1520-0493(1968)096<0833:COTLLJ>2.0.CO;2, 1968.
Byerle, L. A. and Paegle, J.: Modulation of the Great Plains low-level jet and moisture transports by orography and large-scale circulations, J. Geophys. Res.-Atmos., 108, GCP 6-1–GCP 6-16, https://doi.org/10.1029/2002JD003005, 2003.
Chen, M., Shi, W., Xie, P., Silva, V. B. S., Kousky, V. E., Higgins, R. W., and Janowiak, J. E.: Assessing objective techniques for gauge-based analyses of global daily precipitation, J. Geophys. Res.-Atmos., 113, 1–13, https://doi.org/10.1029/2007JD009132, 2008.
Cook, K. H., Vizy, E. K., Launer, Z. S., and Patricola, C. M.: Springtime intensification of the great plains low-level jet and midwest precipitation in GCM Simulations of the twenty-first century, J. Climate, 21, 6321–6340, https://doi.org/10.1175/2008JCLI2355.1, 2008.
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011.
Dong, X., Xi, B., Kennedy, A., Feng, Z., Entin, J. K., Houser, P. R., Schiffer, R. A., L'Ecuyer, T., Olson, W. S., Hsu, K. L., Liu, W. T., Lin, B., Deng, Y., and Jiang, T.: Investigation of the 2006 drought and 2007 flood extremes at the Southern Great Plains through an integrative analysis of observations, J. Geophys. Res.-Atmos., 116, D03204, https://doi.org/10.1029/2010JD014776, 2011.
Drumond, A., Nieto, R., Trigo, R., Ambrizzi, T., Souza, E., and Gimeno, L.: A lagrangian identification of the main sources of moisture affecting northeastern Brazil during its pre-rainy and rainy seasons, PLoS One, 5, 1–8, https://doi.org/10.1371/journal.pone.0011205, 2010.
Dudhia, J.: Numerical Study of Convection Observed during the Winter Monsoon Experiment Using a Mesoscale Two-Dimensional Model, J. Atmos. Sci., 46, 3077–3107, https://doi.org/10.1175/1520-0469(1989)046<3077:NSOCOD>2.0.CO;2, 1989.
Eiras-Barca, J., Dominguez, F., Hu, H., Garaboa-Paz, D., and Miguez-Macho, G.: Evaluation of the moisture sources in two extreme landfalling atmospheric river events using an Eulerian WRF tracers tool, Earth Syst. Dynam., 8, 1247–1261, https://doi.org/10.5194/esd-8-1247-2017, 2017.
Gimeno, L., Stohl, A., Trigo, R. M., Dominguez, F., Yoshimura, K., Yu, L., Drumond, A., Durán-Quesada, A. M., and Nieto, R.: Oceanic and terrestrial sources of continental precipitation, Rev. Geophys., 50, RG4003, https://doi.org/10.1029/2012RG000389, 2012.
Harding, K. J. and Snyder, P. K.: Examining future changes in the character of central U.S. warm-season precipitation using dynamical downscaling, J. Geophys. Res., 119, 13113–16136, https://doi.org/10.1002/2014JD022575, 2014.
Helfand, H. M. and Schubert, S. D.: Climatology of the simulated Great Plains low-level jet and its contribution to the continental moisture budget of the United States, J. Climate, 8, 784–806, https://doi.org/10.1175/1520-0442(1995)008<0784:COTSGP>2.0.CO;2, 1995.
Higgins, R. W., Mo, K. C., and Schubert, S. D.: The moisture budget of the central United States in spring as evaluated in the NCEP/NCAR and the NASA/DAO reanalyses, Mon. Weather Rev., 124, 939–963, https://doi.org/10.1175/1520-0493(1996)124<0939:TMBOTC>2.0.CO;2, 1996.
Higgins, R. W., Yao, Y., Yarosh, E. S., Janowiak, J. E., and Mo, K. C.: Influence of the great plains low-level jet on summertime precipitation and moisture transport over the central United States, J. Climate, 10, 481–507, https://doi.org/10.1175/1520-0442(1997)010<0481:IOTGPL>2.0.CO;2, 1997.
Hong, S. and Lim, J.: The WRF single-moment 6-class microphysics scheme (WSM6), J. Korean Meteor. Soc., 42, 129–151, 2006.
Hu, Q., Jiang, D., and Lang, X.: Sources of moisture for different intensities of summer rainfall over the Chinese Loess Plateau during 1979–2009, Int. J. Climatol., 38, e1280–e1287, https://doi.org/10.1002/joc.5416, 2018.
Hu, X. M., Klein, P. M., and Xue, M.: Evaluation of the updated YSU planetary boundary layer scheme within WRF for wind resource and air quality assessments, J. Geophys. Res.-Atmos., 118, 10490–10505, https://doi.org/10.1002/jgrd.50823, 2013.
Insua-Costa, D. and Miguez-Macho, G.: A new moisture tagging capability in the Weather Research and Forecasting model: formulation, validation and application to the 2014 Great Lake-effect snowstorm, Earth Syst. Dynam., 9, 167–185, https://doi.org/10.5194/esd-9-167-2018, 2018.
Kain, J. S.: The Kain–Fritsch Convective Parameterization: An Update, J. Appl. Meteorol., 43, 170–181, https://doi.org/10.1175/1520-0450(2004)043<0170:TKCPAU>2.0.CO;2, 2004.
Miguez-Macho, G., Rios-Entenza, A., and Dominguez, F.: The impact of soil moisture and evapotranspiration fluxes on the spring water cycle in the Iberian Peninsula: A study with moisture tracers in WRF, in: AGU Fall Meeting Abstracts, 2013.
Mlawer, E. J., Taubman, S. J., Brown, P. D., Iacono, M. J., and Clough, S. A.: Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave, J. Geophys. Res.-Atmos., 102, 16663–16682, https://doi.org/10.1029/97JD00237, 1997.
Mo, K. C. and Juang, H.-M. H.: Relationships between soil moisture and summer precipitation over the Great Plains and the Southwest, J. Geophys. Res.-Atmos., 108, GCP 5-1–GCP 5-17, https://doi.org/10.1029/2002JD002952, 2003.
Mo, K. C., Nogues-Paegle, J., and Paegle, J.: Physical mechanisms of the 1993 summer floods, J. Atmos. Sci., 52, 879–895, https://doi.org/10.1175/1520-0469(1995)052<0879:PMOTSF>2.0.CO;2, 1995.
Mo, K. C., Paegle, J. N., and Higgins, R. W.: Atmospheric processes associated with summer floods and droughts in the central United States, J. Climate, 10, 3028–3046, https://doi.org/10.1175/1520-0442(1997)010<3028:APAWSF>2.0.CO;2, 1997.
Moore, B. J., Neiman, P. J., Ralph, F. M., and Barthold, F. E.: Physical Processes Associated with Heavy Flooding Rainfall in Nashville, Tennessee, and Vicinity during 1–2 May 2010: The Role of an Atmospheric River and Mesoscale Convective Systems, Mon. Weather Rev., 140, 358–378, https://doi.org/10.1175/MWR-D-11-00126.1, 2012.
Nakamura, J., Lall, U., Kushnir, Y., Robertson, A. W., and Seager, R.: Dynamical Structure of Extreme Floods in the U.S. Midwest and the United Kingdom, J. Hydrometeorol., 14, 485–504, https://doi.org/10.1175/JHM-D-12-059.1, 2013.
Nayak, M. A., Villarini, G., Bradley, A. A., Nayak, M. A., Villarini, G., and Bradley, A. A.: Atmospheric Rivers and Rainfall during NASA's Iowa Flood Studies (IFloodS) Campaign, J. Hydrometeorol., 17, 257–271, https://doi.org/10.1175/JHM-D-14-0185.1, 2016.
Numaguti, A.: Origin and recycling processes of precipitating water over the Eurasian continent: Experiments using an atmospheric general circulation model, J. Geophys. Res.-Atmos., 104, 1957–1972, https://doi.org/10.1029/1998JD200026, 1999.
Pan, Z., Segal, M., and Arritt, R. W.: Role of Topography in Forcing Low-Level Jets in the Central United States during the 1993 Flood-Altered Terrain Simulations, Mon. Weather Rev., 132, 396–403, https://doi.org/10.1175/1520-0493(2004)132<0396:ROTIFL>2.0.CO;2, 2004.
Pu, B., Dickinson, R. E., and Fu, R.: Dynamical connection between Great Plains low-level winds and variability of central Gulf States precipitation, J. Geophys. Res.-Atmos., 121, 3421–3434, https://doi.org/10.1002/2015JD024045, 2016.
Ramos, A. M., Nieto, R., Tomé, R., Gimeno, L., Trigo, R. M., Liberato, M. L. R., and Lavers, D. A.: Atmospheric rivers moisture sources from a Lagrangian perspective, Earth Syst. Dynam., 7, 371–384, https://doi.org/10.5194/esd-7-371-2016, 2016.
Rife, D. L., Pinto, J. O., Monaghan, A. J., Davis, C. A., and Hannan, J. R.: Global distribution and characteristics of diurnally varying low-level jets, J. Climate, 23, 5041–5064, https://doi.org/10.1175/2010JCLI3514.1, 2010.
Schubert, S. D., Helfand, H. M., Wu, C. Y., and Min, W.: Subseasonal variations in warm-season moisture transport and precipitation over the central and eastern United States, J. Climate, 11, 2530–2555, https://doi.org/10.1175/1520-0442(1998)011<2530:SVIWSM>2.0.CO;2, 1998.
Shin, H. H. and Hong, S. Y.: Intercomparison of Planetary Boundary-Layer Parametrizations in the WRF Model for a Single Day from CASES-99, Bound.-Lay. Meteorol., 139, 261–281, https://doi.org/10.1007/s10546-010-9583-z, 2011.
Sorí, R., Marengo, J., Nieto, R., Drumond, A., and Gimeno, L.: The Atmospheric Branch of the Hydrological Cycle over the Negro and Madeira River Basins in the Amazon Region, Water, 10, 738, https://doi.org/10.3390/w10060738, 2018.
Stensrud, D. J.: Importance of low-level jets to climate: A review, J. Climate, 9, 1698–1711, https://doi.org/10.1175/1520-0442(1996)009<1698:IOLLJT>2.0.CO;2, 1996.
Stohl, A., James, P., Stohl, A., and James, P.: A Lagrangian Analysis of the Atmospheric Branch of the Global Water Cycle. Part I: Method Description, Validation, and Demonstration for the August 2002 Flooding in Central Europe, J. Hydrometeorol., 5, 656–678, https://doi.org/10.1175/1525-7541(2004)005<0656:ALAOTA>2.0.CO;2, 2004.
Stohl, A. and James, P.: A Lagrangian Analysis of the Atmospheric Branch of the Global Water Cycle. Part II: Moisture Transports between Earth's Ocean Basins and River Catchments, J. Hydrometeorol., 6, 961–984, https://doi.org/10.1175/JHM470.1, 2005a.
Stohl, A., Forster, C., Frank, A., Seibert, P., and Wotawa, G.: Technical note: The Lagrangian particle dispersion model FLEXPART version 6.2, Atmos. Chem. Phys., 5, 2461–2474, https://doi.org/10.5194/acp-5-2461-2005, 2005b.
Stohl, A., Forster, C., and Sodemann, H.: Remote sources of water vapor forming precipitation on the Norwegian west coast at 60∘ N – A tale of hurricanes and an atmospheric river, J. Geophys. Res.-Atmos., 113, 1–13, https://doi.org/10.1029/2007JD009006, 2008.
Tang, Y., Winkler, J., Zhong, S., Bian, X., Doubler, D., Yu, L., and Walters, C.: Future changes in the climatology of the Great Plains low-level jet derived from fine resolution multi-model simulations, Sci. Rep., 7, 5029, https://doi.org/10.1038/s41598-017-05135-0, 2017.
Ting, M. and Wang, H.: The Role of the North American Topography on the Maintenance of the Great Plains Summer Low-Level Jet, J. Atmos. Sci., 63, 1056–1068, https://doi.org/10.1175/JAS3664.1, 2006.
Trenberth, K. E. and Guillemot, C. J.: Physical processes involved in the 1988 drought and 1993 floods in north America, J. Climate, 9, 1288–1298, https://doi.org/10.1175/1520-0442(1996)009<1288:PPIITD>2.0.CO;2, 1996.
Vázquez, M., Nieto, R., Drumond, A., and Gimeno, L.: Moisture transport into the Arctic: Source-receptor relationships and the roles of atmospheric circulation and evaporation, J. Geophys. Res.-Atmos., 121, 13493–13509, https://doi.org/10.1002/2016JD025400, 2016.
Walters, C. K., Winkler, J. A., Shadbolt, R. P., van Ravensway, J., and Bierly, G. D.: A long-term climatology of southerly and northerly low-level jets for the central United States, Ann. Assoc. Am. Geogr., 98, 521–552, https://doi.org/10.1080/00045600802046387, 2008.
Wang, S. Y. and Chen, T. C.: The late-spring maximum of rainfall over the U.S. central plains and the role of the low-level jet, J. Climate, 22, 4696–4709, https://doi.org/10.1175/2009JCLI2719.1, 2009.
Wegmann, M., Orsolini, Y., Vázquez, M., Gimeno, L., Nieto, R., Bulygina, O., Jaiser, R., Handorf, D., Rinke, A., Dethloff, K., Sterin, A., and Brönnimann, S.: Arctic moisture source for Eurasian snow cover variations in autumn, Environ. Res. Lett., 10, 054015, https://doi.org/10.1088/1748-9326/10/5/054015, 2015.
Wexler, H.: A Boundary Layer Interpretation of the Low-level Jet, Tellus, 13, 368–378, https://doi.org/10.1111/j.2153-3490.1961.tb00098.x, 1961.
Wu, Y. and Raman, S.: The summertime Great Plains low level jet and the effect of its origin on moisture transport, Bound.-Lay. Meteorol., 88, 445–466, https://doi.org/10.1023/A:1001518302649, 1998.